5.4中心对称

(共30张PPT)
请欣赏下列美丽的图案
将上述图形绕其上的某一点旋转180o,这些图形与原来的图形能够完全重合吗？
思考:
C
O/
D
A
B
C
A
B
O/
C
O/
D
A
B
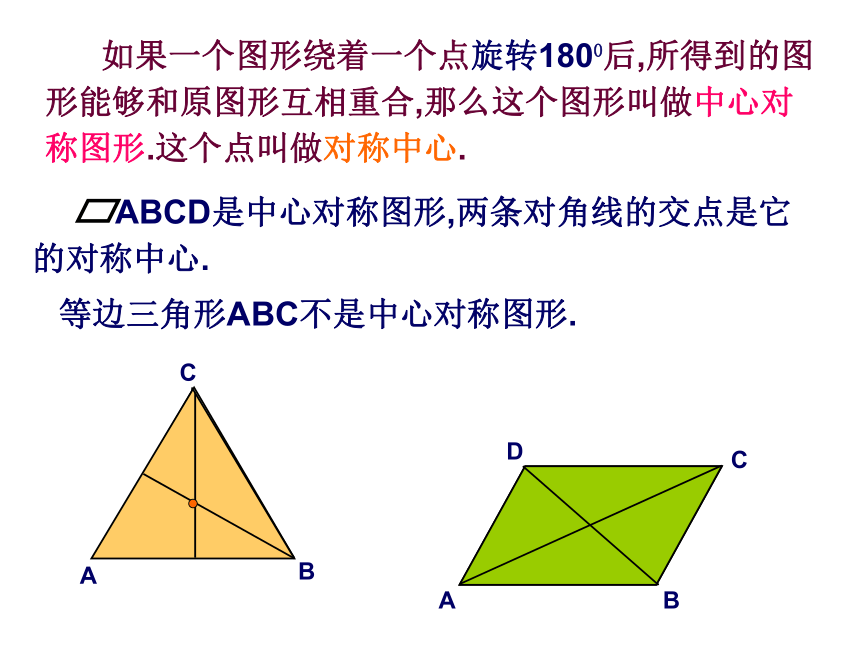
如果一个图形绕着一个点旋转1800后,所得到的图形能够和原图形互相重合,那么这个图形叫做中心对称图形.这个点叫做对称中心.
等边三角形ABC不是中心对称图形.
ABCD是中心对称图形,两条对角线的交点是它的对称中心.
C
A
B
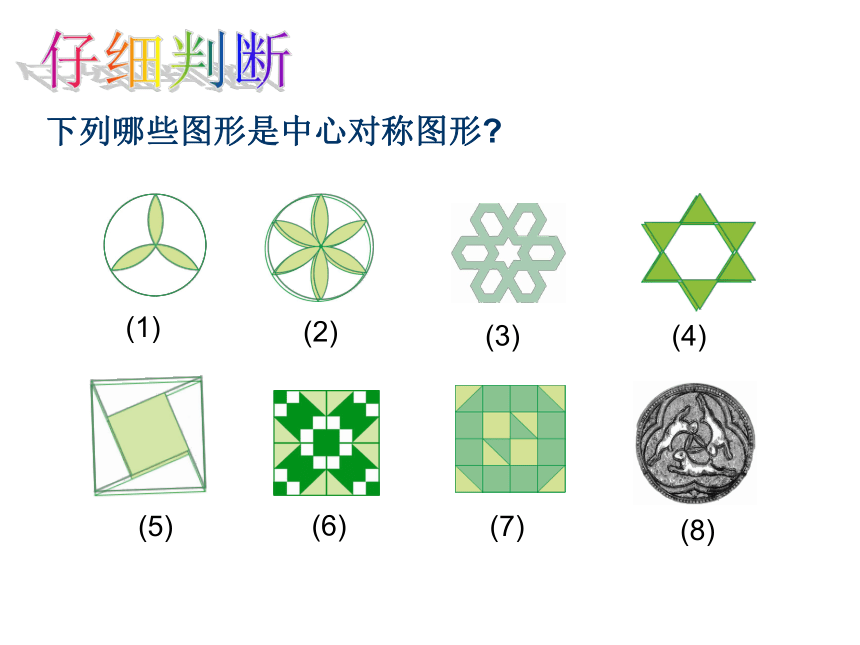
下列哪些图形是中心对称图形
(1)
(8)
(7)
(6)
(5)
(4)
(3)
(2)
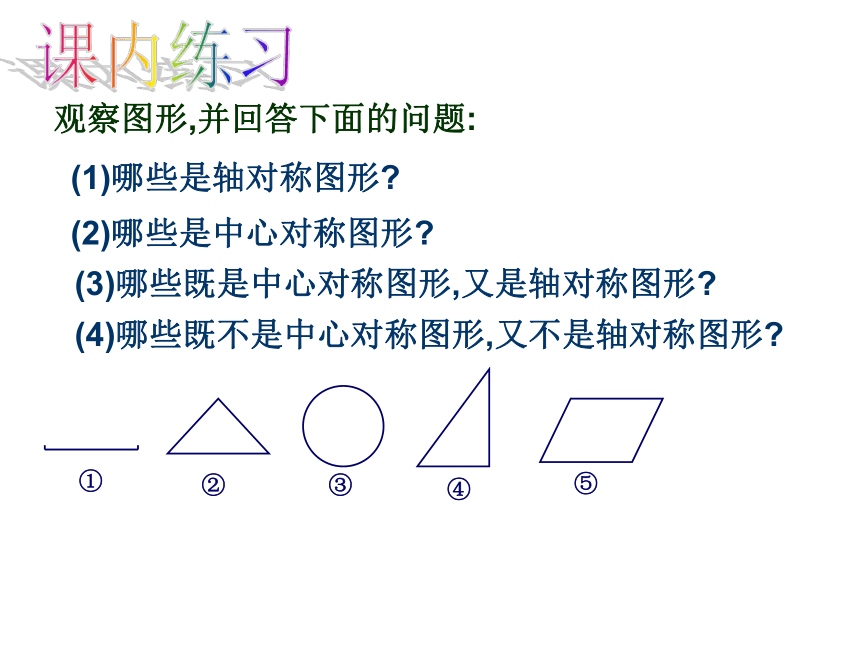
观察图形,并回答下面的问题:
(1)哪些是轴对称图形
(2)哪些是中心对称图形
(3)哪些既是中心对称图形,又是轴对称图形
(4)哪些既不是中心对称图形,又不是轴对称图形
①
②
③
④
⑤
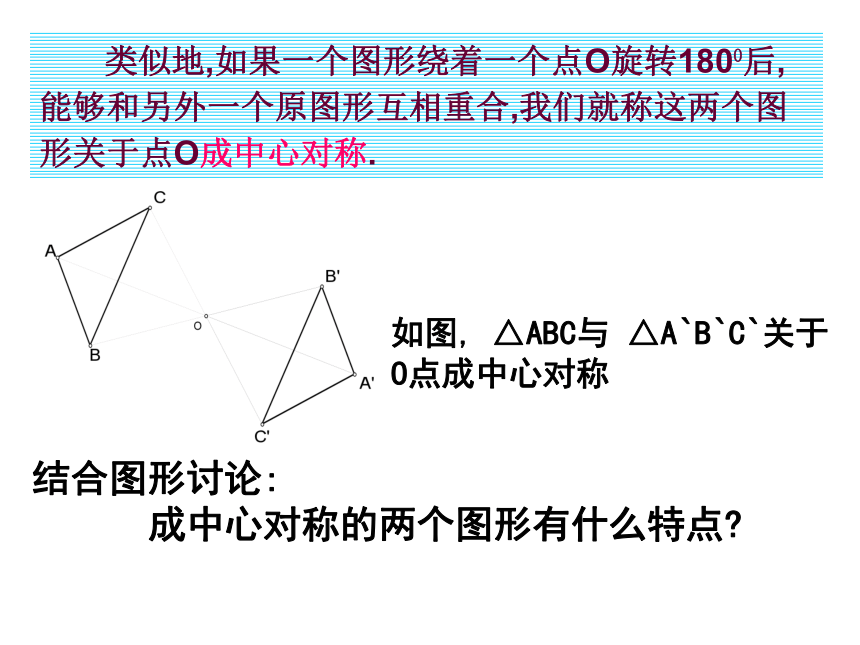
类似地,如果一个图形绕着一个点O旋转1800后,能够和另外一个原图形互相重合,我们就称这两个图形关于点O成中心对称.
结合图形讨论:
成中心对称的两个图形有什么特点
如图, △ABC与 △A`B`C`关于
O点成中心对称
*
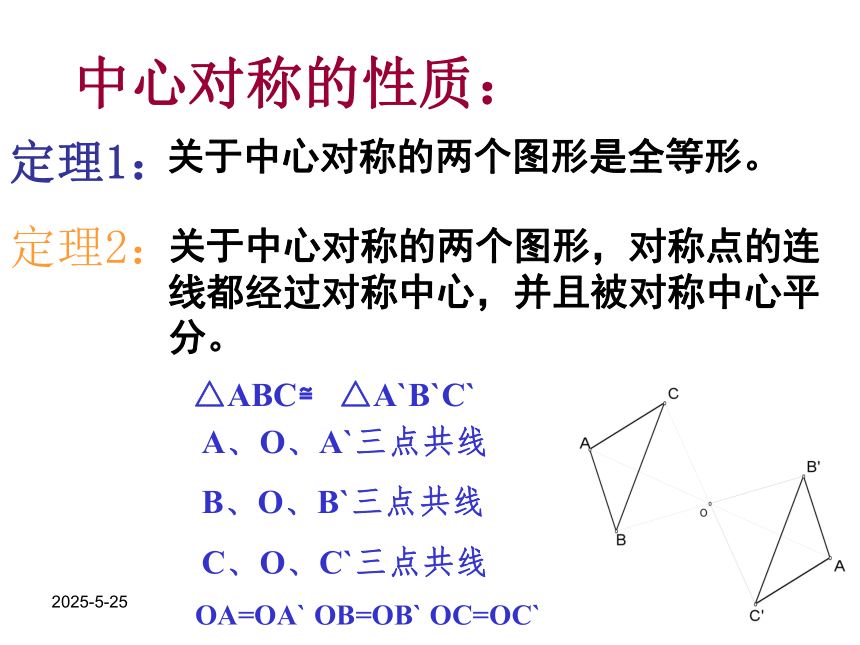
关于中心对称的两个图形，对称点的连线都经过对称中心，并且被对称中心平分。
中心对称的性质：
定理1：
定理2：
关于中心对称的两个图形是全等形。
△ABC≌ △A`B`C`
A、O、A`三点共线
B、O、B`三点共线
C、O、C`三点共线
OA=OA` OB=OB` OC=OC`
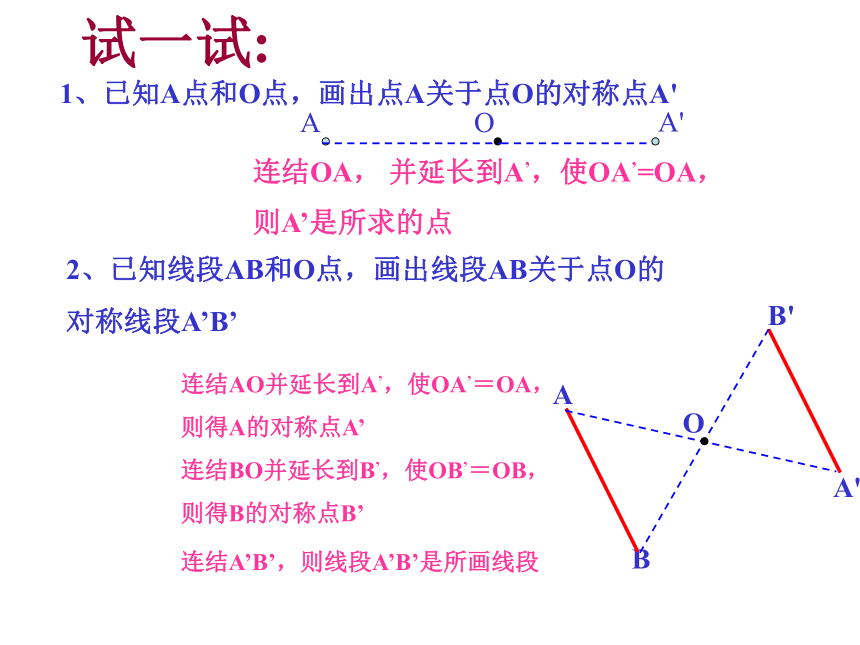
试一试:
A
O
A'
连结OA，
并延长到A’，使OA’=OA，
1、已知A点和O点，画出点A关于点O的对称点A'
则A’是所求的点
2、已知线段AB和O点，画出线段AB关于点O的
对称线段A’B’
O
A'
B'
A
B
连结AO并延长到A’，使OA’＝OA，
则得A的对称点A’
连结BO并延长到B’，使OB’＝OB，
则得B的对称点B’
连结A’B’，则线段A’B’是所画线段
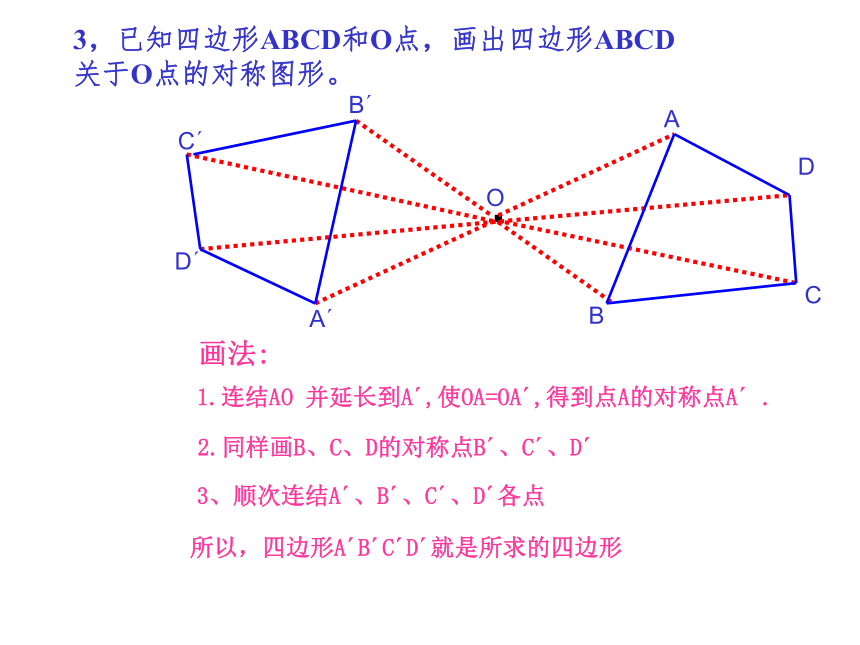
3，已知四边形ABCD和O点，画出四边形ABCD
关于O点的对称图形。
.
C
D
A
B
D
C
O
A
B
画法:
1.连结AO 并延长到A ,使OA=OA ,得到点A的对称点A .
2.同样画B、C、D的对称点B 、C 、D
3、顺次连结A 、B 、C 、D 各点
所以，四边形A B C D 就是所求的四边形
*
中心对称的特征与实际应用
具有数学美。因为中心对称图形形状匀称美观。所以许多建筑、工艺品、商标常用这种图形作装饰图案。
平稳旋转。具有中心对称图形形状的物体，能够在所在的平面内绕对称中心平稳旋转。所以在生产中，有关旋转的零部件常设计成中心对称图形。
上图表示一根弦的分段振动和整体振动。
*
小结:
通过这节课的学习,请大家说说
你的收获与困惑!
雅致
*
中心对称 轴对称
1
2
3 有一个对称中心—点
图形绕中心旋转180
旋转后与另一图形重合 有一条对称轴—线
图形沿轴对折180
翻折后与另一图形重合
°
中心对称与轴对称的类比
°
名称
图形 中心对称图形 轴对称图形 对称中心，对称轴
线
段
角
等腰三角形
平行四边形
是
是
是
是
不是
不是
不是
是
线段中点
线段的中垂线和线段本身所在的直线
角平分线所在的直线
底边的中垂线
对角线交点
名称
图形
中心对称图形
轴对称图形
对称中心，对称轴
矩形
菱形
正方形
圆
等腰梯形
是
是
是
是
是
是
是
是
是
不是
圆心
边的中垂线
对角线交点
对角线交点
对角线所在直线
对角线交点
对角线所在直线
边的中垂线
直径所在直线
两底的中垂线
南苑中学搞绿化,要在一块圆形的空地上
建花坛,现征集设计图案
要求:设计的方案必须由圆形和正方形组成
(个数不限)并使整个图案呈中心对称
图形,请画出你的设计方案,并为你
的设计图想个适当的名称,与你的同
学共同分享.
再见
书本作业题及作业本.