直线与圆.圆与圆位置关系复习课件2

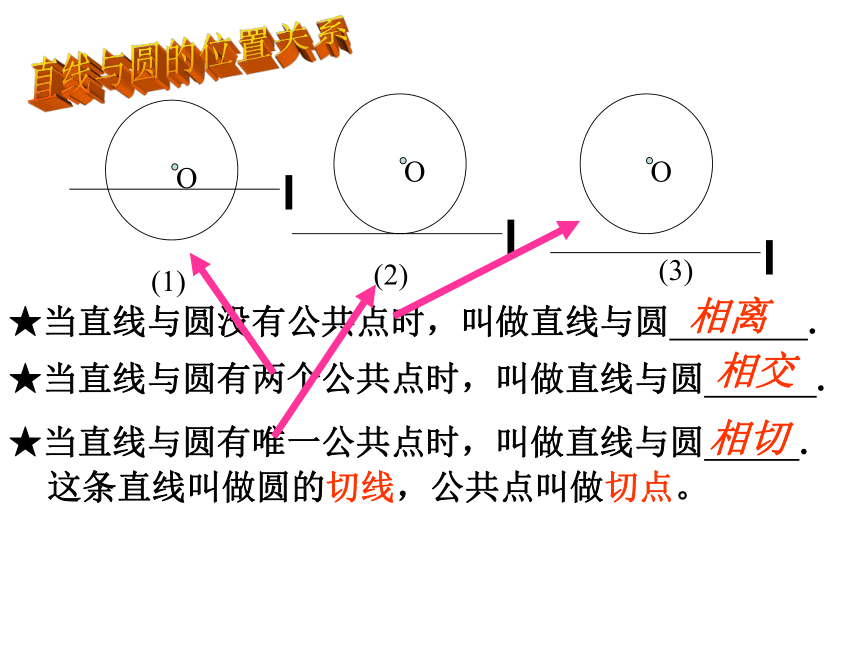
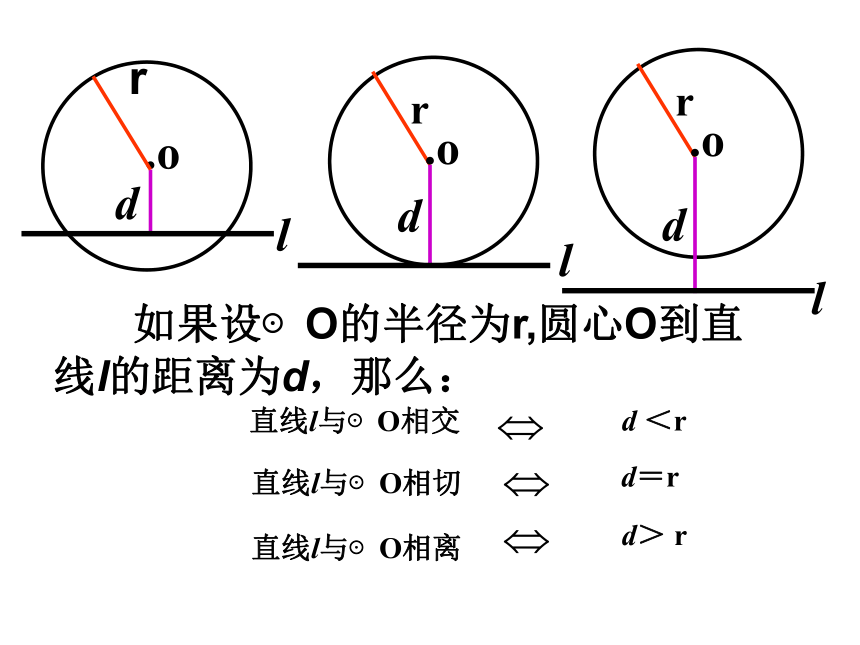
课件19张PPT。第三章 直线与圆、圆与圆的位置关系复习 ------ 朱勇玲直线与圆位置关系圆与圆位置关系相离相切相交 判定性质相离相切相交★当直线与圆有唯一公共点时，叫做直线与圆 .★当直线与圆没有公共点时，叫做直线与圆 . ★当直线与圆有两个公共点时，叫做直线与圆 . 相离相切相交直线与圆的位置关系(1)(3)(2)这条直线叫做圆的切线，公共点叫做切点。OOOlll.orddd 如果设⊙O的半径为r,圆心O到直线l的距离为d，那么：lll直线l与⊙O相交d ＜r 直线l与⊙O相切d＝r直线l与⊙O相离d＞ r
1、 ⊙o的直径是3，直线与⊙o相交，圆心o到直线的距离是d，则d应满足 ( )
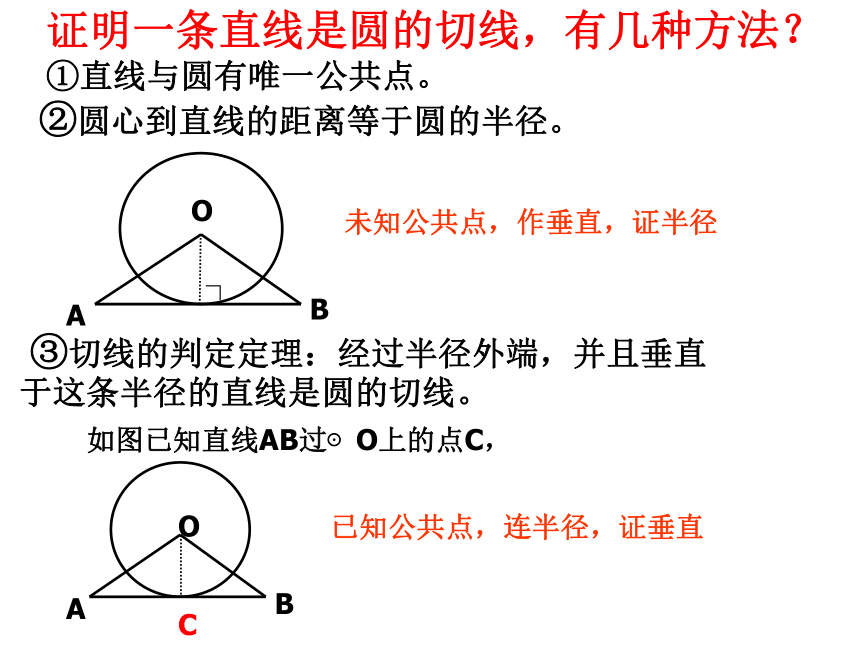
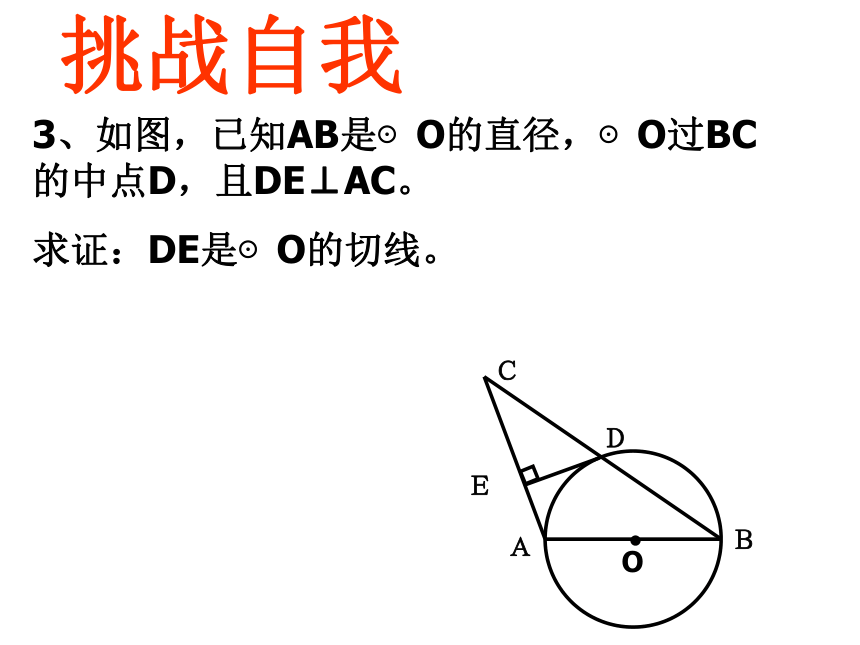
A. d>3 B. 1.52、已知⊙o的半径是r,点o到直线l的距离为d,若d,r满足 ︱8-2r︱=0,则直线与⊙o的交点个数是 ______c1个做一做如图已知直线AB过⊙O上的点C，已知公共点，连半径，证垂直未知公共点，作垂直，证半径证明一条直线是圆的切线，有几种方法？①直线与圆有唯一公共点。②圆心到直线的距离等于圆的半径。 ③切线的判定定理：经过半径外端，并且垂直于这条半径的直线是圆的切线。∟3、如图，已知AB是⊙O的直径，⊙O过BC的中点D，且DE⊥AC。
求证：DE是⊙O的切线。挑战自我如图，已知AB是⊙O的直径，⊙O过BC的中点D，且DE⊥AC。
求证：DE是⊙O的切线。OＡＢＣＤＥ证：连DO∵AO=BO,CD=BD∴DO是△ABC的中位线∴DO∥AC又∵ DE⊥AC∴ DE⊥DO∴ DE是⊙O的切线切线的性质：切线的性质可归纳为：
1、过圆心 2、过切点 3、垂直于切线
选取其中任意两个作为题设，第三个便是结论。5. 如图：已知PA，PB分别切⊙O于A，B两点，如果∠P=60° ，PA=2，那么AB的长为_____.2变式1:CD也与⊙O相切,切点为E.交PA于C点，交PB于D点，则△ PCD的周长为____.4变式2：若PA=a,则△ PCD的周长为____.
2a在经过圆外一点的切线上，这一点与切点之
间的线段的长叫做这点到圆的切线长。切线长定理：从圆外一点引圆的两条切线，
他们的切线长相等。结论：定义1、定义：和三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，三角形的内心是三角形的三条角平分线的交点，这个三角形叫做圆的外切三角形。2、性质: 内心到三角形三边的距离相等；内心与顶点连线平分内角。三角形的内切圆ABCODEr如：直角三角形的两直角边分别是5cm，12cm 则其内切圆的半径为______。　变式
如图，直角三角形的两直角边分别是a，b,斜边为c 则其内切圆的半径ｒ为:
（以含ａ、ｂ、ｃ的代数式表示ｒ）2cm直线与圆位置关系圆与圆位置关系相离相切相交 判定性质相离相切相交外离内含外切内切外离外切相交内切内含01210R-rr)(R>r)两圆位置关系的性质与判定d>R+rd=R+r1、若两圆有唯一公共点，且两圆半径分别为5和2，则两圆圆心距为 。2、已知，两圆相外切，半径分别是1㎝和2㎝，要作和这两个已知圆都相切且半径等于3㎝的圆，可作_____个。7或３5
3、如图，已知⊙O1与⊙O2交于A，B两点，过A的直线交两圆于C，D两点，G为CD的中点，BG及其延长线交⊙O1，⊙O2于E，F，连结DF，CE，求证：CE=DF．
闯一闯直线与圆位置关系圆与圆位置关系相离相切相交 判定性质（切线长定理，三角形的内切圆）相离相切相交外离内含外切内切小结：作业：见练习纸
再 见！