2.6勾股定理探索

课件15张PPT。 2.6探索勾股定理（1）“引葭赴岸”是《九章算术》中的一道题：
“今有池一丈，葭生其中央，出水一尺，
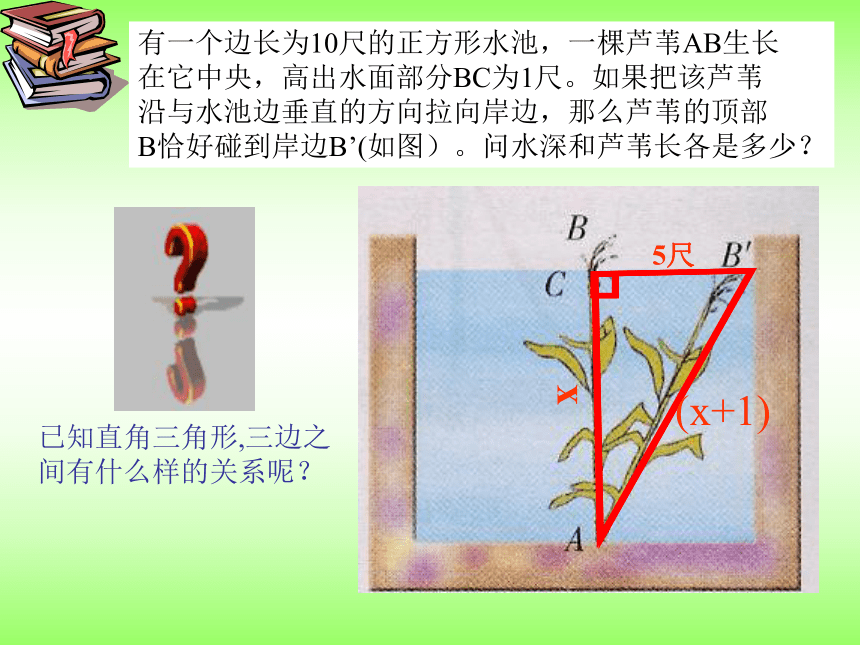
引葭赴岸，适与岸齐。问水深，葭各长几何？”有一个边长为10尺的正方形水池，一棵芦苇AB生长
在它中央，高出水面部分BC为1尺。如果把该芦苇
沿与水池边垂直的方向拉向岸边，那么芦苇的顶部
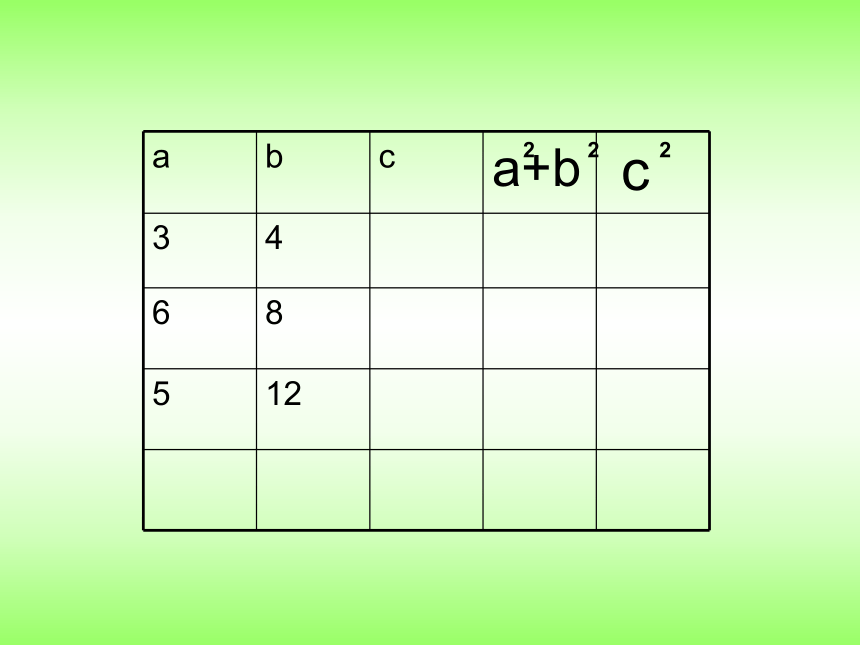
B恰好碰到岸边B’(如图）。问水深和芦苇长各是多少？已知直角三角形,三边之间有什么样的关系呢？5尺x(x+1)合作学习（1）作三个直角三角形，使其两直角边分别是3cm和4cm,6cm和8cm，5cm和12cm,
(2)分别测量三个直角三角形的斜边的长度，并完成下表。
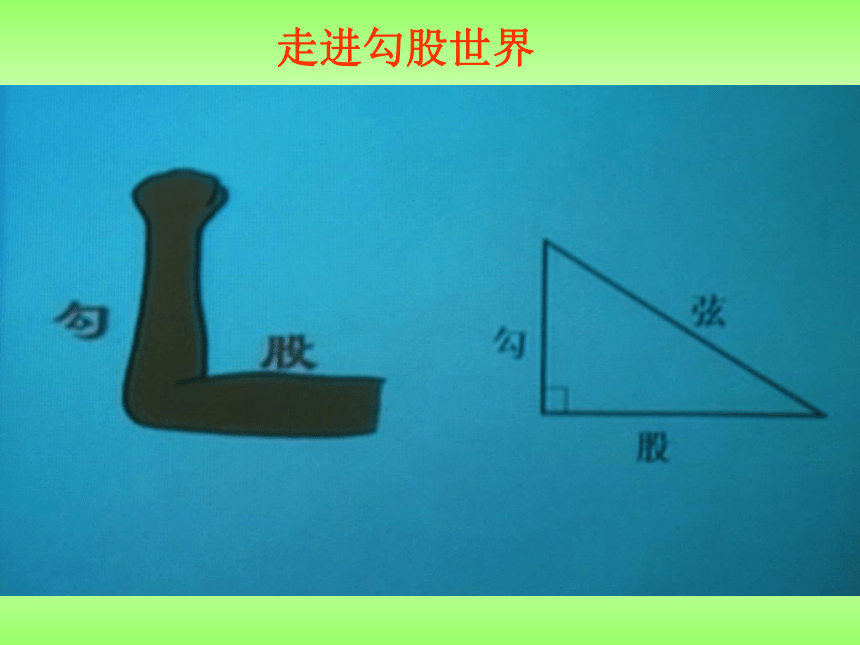
（3）你能发现直角三角形三边长度之间存在什么关系吗？动画222 勾股定理如果直角三角形两直角边分别为
a、b,斜边为c，那么 直角三角形两直角边的平方和等于斜边的平方。勾股弦走进勾股世界读一读 勾股世界
我国是最早了解勾股定理的国家之一。早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角三角形，如果勾等于三，股等于四，那么弦就等于五。即“勾三、股四、弦五”。它被记载于我国古代著名的数学著作《周髀算经》中。在这本书中的另一处，还记载了勾股定理的一般形式。
1945年，人们在研究古巴比伦人遗留下的一块数学泥板时，惊讶地发现上面竟然刻有15组能构成直角三角形三边的数，其年代远在商高之前。
相传二千多年前，希腊的毕达哥拉斯学派首先证明了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯定理。利用拼图来验证勾股定理：1、准备四个全等的直角三角形（设直角三角形的两条直角边分别为a，b，斜边c）；2、你能用这四个直角三角形拼成一个正方形吗？拼一拼试试看3、你拼的正方形中是否含有以斜边c为边的正方形？4、你能否就你拼出的图说明a2+b2=c2？∵ c2= 4?ab/2 +(b-a)2 =2ab+b2-2ab+a2 =a2+b2∴a2+b2=c2大正方形的面积可以表示为 ；
也可以表示为c24?ab/2+(b- a)2
∵ (a+b)2 = c2 + 4?ab/2a2+2ab+b2 = c2 +2ab∴a2+b2=c2大正方形的面积可以表示为 ；
也可以表示为(a+b)2c2 +4?ab/2例1、已知△ABC中, ∠C=Rt∠,BC=a,AC=b,AB=C
已知: a=1, b=2, 求c;
已知: a=15, c=17, 求b;
(4)已知:c=17,a:b=8:15,求a,b.
C例2、 如图所示是一个长方形零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)1. 一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少? ABC算一算例3 、用刻度尺和圆规作一条线段,使它的长度
为√5cm练习：利用作直角三角形，在数轴上表示点√13谈收获布置作业