第五章平行四边形的复习

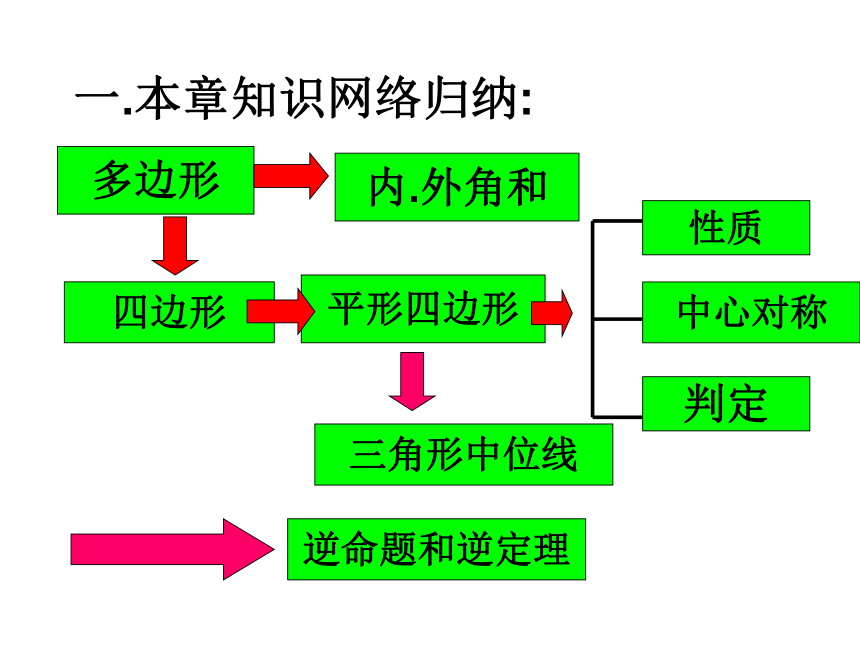
课件38张PPT。第5章 平行四边形复习一.本章知识网络归纳:多边形内.外角和四边形平形四边形三角形中位线逆命题和逆定理二.重要知识规律总结:1.多边形的对角线. n边形从一个顶点出发的对角线有(n－3)条(n≥3).n边形的内角和为：（n－2)×180°(n≥3).2.多边形的内角和公式.n边形共有对角线 条(n≥3)正n边形的每个内角3.平行四边形的性质有：平行四边形的对边相等平行四边形的对边平行平行四边形的对角相等平行四边形的对角线互相平分定理2：两组对边分别相等的四边形是平行四边形定义: 两组对边分别平行的四边形是平行四边形定理1: 一组对边平行且相等的四边形平行四边形 4.平行四边形的判定:定理3：对角线互相平分的四边形是平行四边形．两组对角分别相等的四边形是平行四边形.(补充)数学语言：∵AB∥CD AD ∥ BC ∴四边形ABCD是平行四边形数学语言：∵AB∥CD AB =DC ∴四边形ABCD是平行四边形数学语言：∵AB=CD AD = BC ∴四边形ABCD是平行四边形数学语言：∵AO=CO OD = BO ∴四边形ABCD是平行四边形　 三角形的中位线平行于第三边，并且等于第三边的一半.5.三角形的中位线6.逆命题与逆定理.1、某人到瓷砖商店去购买一种多边形形状的瓷砖，用来铺设无缝地板．他购买的瓷砖形状不可以是（ ）．
（A）正三角形 （B）正四边形 （C）正八边形 （D）正六边形 C试一试2.在平行四边形ABCD中,AC=10,BD=8,则AB的取值范围是( )
A、2 2 D、AB< 93.平行四边形一边长为 10 ,则它的两条对角线可以是( )
A、6 ,8 B、8, 12
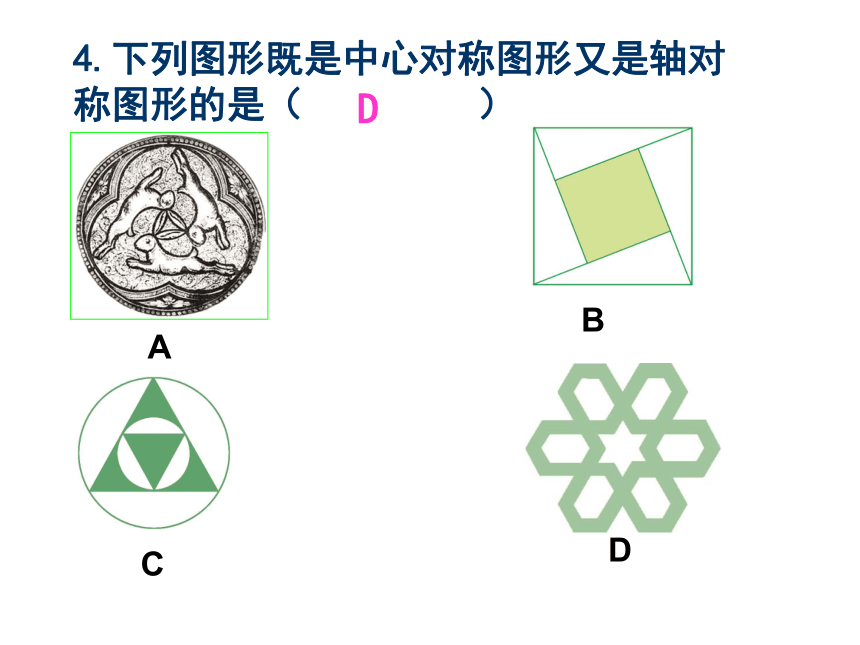
C、8, 14 D、6, 14BC4.下列图形既是中心对称图形又是轴对
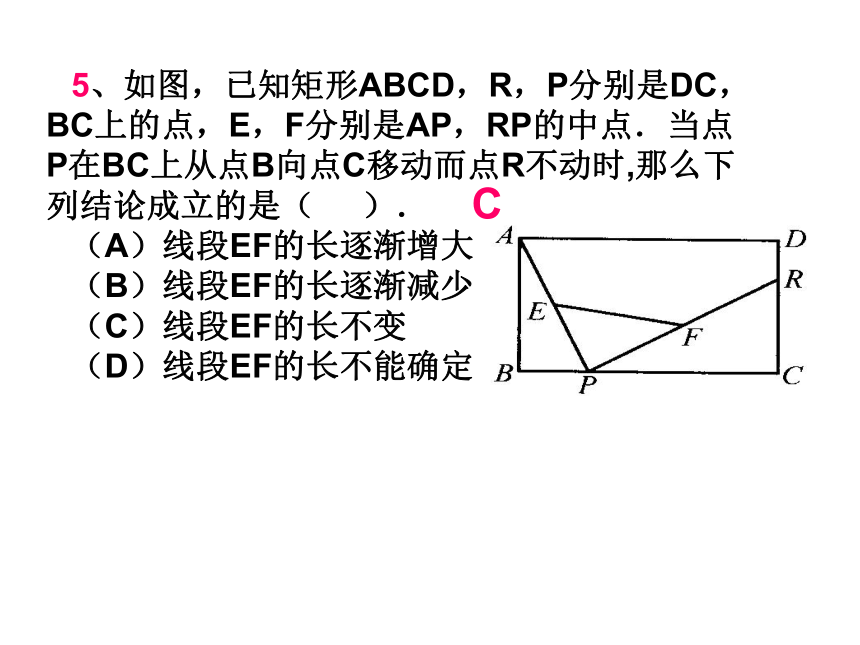
称图形的是（ ）ABCDD5、如图，已知矩形ABCD，R，P分别是DC，BC上的点，E，F分别是AP，RP的中点．当点P在BC上从点B向点C移动而点R不动时,那么下列结论成立的是（ ）．
（A）线段EF的长逐渐增大
（B）线段EF的长逐渐减少
（C）线段EF的长不变
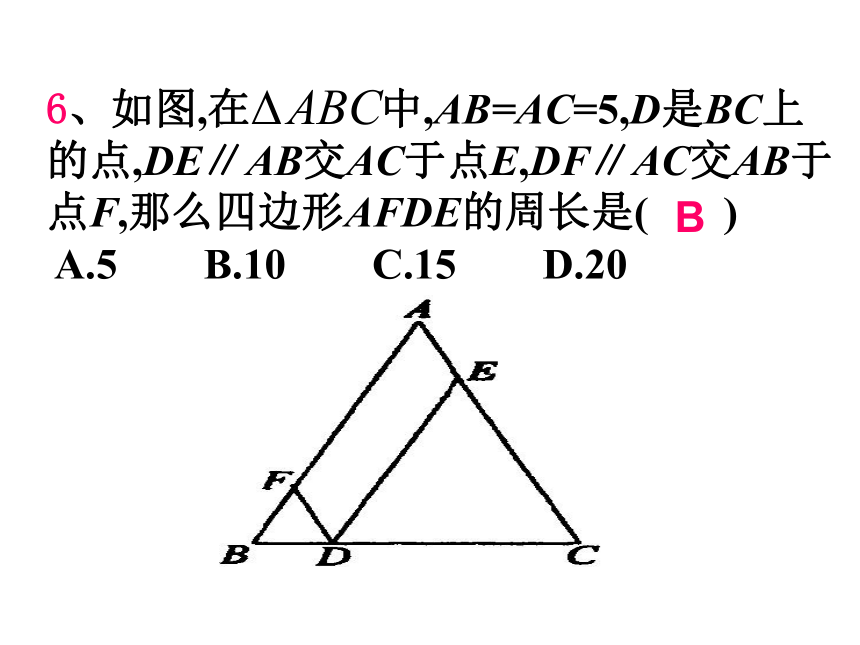
（D）线段EF的长不能确定C6、如图,在 中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是( )
A.5 B.10 C.15 D.20
B7.如图: 在△ABC中, AB = AC = 8,
点D 在BC上, DE∥AC交AB于点E, DF∥AB交AC于F,
则DE＋DF = .ABCDEF188.一个多边形的内角和是外角和的3倍，那么这个
多边形是_____边形; 这个多边形的对角线一共有
_____ ____条.9.从一个多边形的一个顶点出发,一共作了15条对角
线,则这个多边形的内角和为________度.10.已知多边形的每个内角都是156o,则这个多边形是
_________边形.八202880十五11.不能铺满地面的正多边形组合是( )
A. 正三角形和正六边形 B. 正方形和正八边形
C.正三角形和正方形 D.正五边形和正六边形D53130°50°130°D 15. 请你将一个平行四边形分割成面积相等
的四部分.请给出四个不同的分法.
例1.(1)若∠ B=65o,求∠ EAF的度数;(2)若∠ EAF=60o,EC=2,CF=1,
求平行四边形ABCD的周长;(3)若AE=4,AF=6,平行四边形ABCD的周长为40,求
平行四边形ABCD的面积.典型例题 。(补充一个条件)例3. 如图:在 ABCD中, 对角线AC、BD
交于点O,
ABCDO(A) (B)
(C) (D) 2 3

4 5EF则图中共有( )对全等三角形. 6
7 8CBEF过O交AD于E，交BC于F，AB=5， BC=6， OE=2， 则四边形EFCD的周长是 ( ) 13
15 17C55221.如图四边形 ABCD和四边形BFDE都是平行四边形, 求证：AE=CFOO巩固练一练 3. 在四边形ABCD中,若分别给出四个条件:⑴AB∥CD ⑵AD=BC ⑶∠A=∠C ⑷AD∥ BC.现在,以其中的两个为一组,能识别四边形ABCD为平行四边形的条件是 (只填序号) 6.已知：AD为△ABC的角平分线，DE∥AB ，在AB上截取BF＝AE。 求证：EF＝BD1238.请说出“等腰三角形两腰上的高相等”的逆命题．这个逆命题是真命题吗？请证明你的判断. FEDCBA1、如图，在△ABC中， ∠ACB=90o,CD AB于D， ∠BAC的平分线交CD于E，过E点作EF∥AB，交BC于F。求证：CE=FB。⊥∟∟拓展提高ABCDEF1234证明: 在 ABCD中,AD = BC, AB = CD,∠1 = ∠2∵△ADE与△BCF都是正三角形,∴AE=DE=AD, BE=CF=BC,
∠3=∠4=60°.∴DE=BF, AE=CF,
∠1＋∠3=∠2＋∠4,即 ∠EAB=∠DCF,∴△ABE≌△DCF∴BE=DF∴四边形EBFD是平行四边形.3.已知:如图,O是等边三角形ABC内任意一点,OD∥BC,OE∥AC,OF∥AB,点D,E,F分别在AB,BC,AC上.
求证:OD+OE+OF=BC.AFOEDBC4、如图，已知第一个正△A1B1C1的边长为2，分别取△A1B1C1的三边中点A2，B2，C2，作出第二个正△A2B2C2，用同样的方法，作出第三个正△A3B3C3，…，由此可得第n个正△AnBnCn的面积为 。5.已知，在△ABC中，中线BE，CF交于点O，G，H分别是OB，OC的中点，连结GH，EF。求证：FG∥EH6.已知，在△ABC中， AD是中线，点E是AD 的中点，连结CE并延长交AB于F。猜想AF与BF的数量关系？并说明理由7.已知 ABCD中，直线MN // AC，分别交DA延长线于M，DC延长线于N，AB于P，BC于Q。求证：PM=QN。已知 ABCD中，直线MN // AC，分别交DA延长线于M，DC延长线于N，AB于P，BC于Q。求证：PM=QN。已知 ABCD中，直线MN // AC，分别交DA延长线于M，DC延长线于N，AB于P，BC于Q。求证：PM=QN。xyO123-1-27213-1-2-3-348、如图，Rt△OAB的两条直角边在坐标轴上，已知点A（0，2），点B（3，0），则以点O,A,B为其中三个顶点的平行四边形的第四个顶点C的坐标为_________________。ABO-4xyO123-1-27213-1-2-3-349、如图，作直线L，解析式为y=-2x+2，设点M为直线L上一点，过点M作AB的平行线，交y轴于点N，是否存在这样的点M，使得以M、N、A、B为顶点的四边形是平行四边形？若存在，请求出符合条件的点M的坐标；若不存在，请说明理由。ABOL-4体会.分享说能出你这节课的收获和体验让大家与你分享吗？