4.1比例线段（3）

课件23张PPT。4.1比例线段（三）4.1比例线段（三）欣赏之一：古埃及胡夫金字塔欣赏之二:上海东方明珠塔新西兰朝 鲜新加坡中华人民共和国 欣赏之三：国旗中的共同图案。帕特农神庙欣赏之四：上述图形是如此的美丽，我们在欣赏
的时候不禁会想：这些图形为什么会
看起来这么美呢？ 有什么数学原理
在里面呢？判断下列几组数成比例的是:

(1)1,3,3,9

(2)2,3,4,5

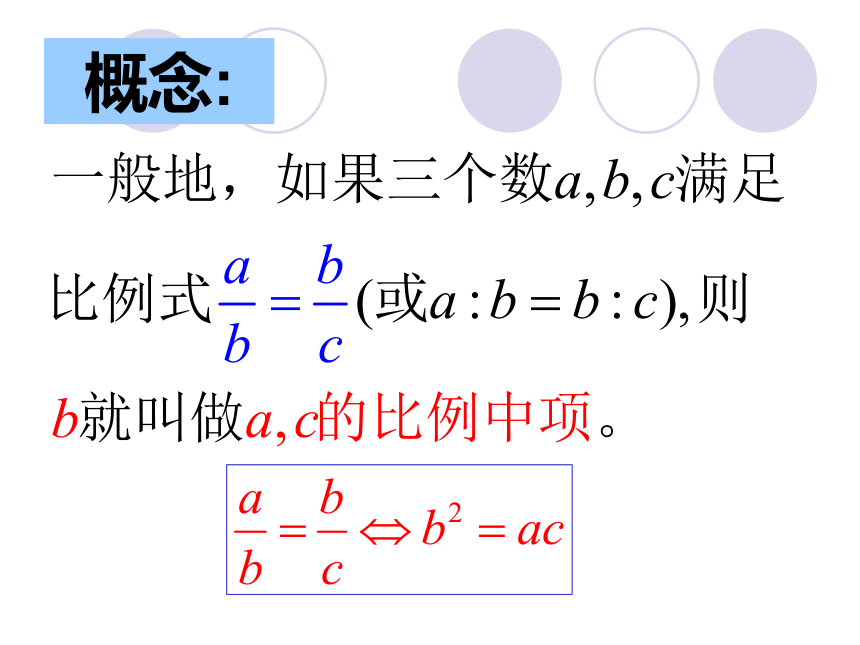
(3)-1,2,2,-4小热身√√×概念:练习1：注意:（1）1是不是 和 的比例中项？答：因为 ，所以1是 和 的比例中项。线段的比例中项是一个正数，而数的比例中项是一对互为相反数。(2) 和 的比例中项是什么？ 答案：（3）若线段a=2cm,b=8cm,则线段a和b的比例中项是什么? 答案：4cm动手画一画如图，画一条线段AB.
（1）你能否在线段AB上找到一点P，使得 ？ （2）能否在线段AB上找到一点P
使得 成立呢？思考:如何求出黄金比的数值?概念：勾股定理和黄金分割是几何中的双宝,
“前者好似黄金，后者堪称珠玉”。你知道吗？练习2：（1）若P是线段AB的黄金分割点（PA＞PB），设AB=10，则PA的长约为 （ ）
A、0.618 B、3.82 C、5 D、6.18
（2）已知线段AB=2cm,点C是线段AB的黄金分割点，
则AC= 　　　　 。
D或作法:（1）过已知线段AB的端点B作BC⊥AB
使
例５：已知线段AB=a，用直尺和圆规作出它的黄金分割点。（2）连接AC，在CA上截取CD=CB（3）在AB上截取AP=AD
问：点P是线段AB唯一的黄金分割点吗欣赏之一：古埃及胡夫金字塔文明古国埃及的金字塔，形似方锥，大小各异。但这些金字塔底面的边长与高之比都接近于0.618.欣赏黄金分割之美468m289.2m上海东方明珠电视塔高468m,上球体到塔底的距离约为289.2m, 289.2与468的比值是一个神奇的数字,这个塔的设计精巧,外型匀称、漂亮、美观、大方.欣赏之二:上海东方明珠塔新西兰朝 鲜新加坡中华人民共和国 欣赏之三：国旗中的共同图案。FHGMN帕特农神庙欣赏之四：黄金矩形：
宽与长的比约为0.618。ＤＣＥEF点F为线段AB的黄金分割点，
点E为线段CD的黄金分割点。黄金分割之美的应用：
人体下本身与身高的比例越接近0.618，越给人美感，遗憾的是，即使是身体修长的芭蕾舞演员也达不到如此的完美。某女士身高1.68米，下半身1.02米，她应该选择多高的高跟鞋看起来更美呢？课堂小结：1.比例中项的概念；
2.线段的比例中项与数的比例中项的区别；
3.黄金分割，黄金分割点，黄金比的概念；
4．黄金分割在生活中的应用。