1.2 有关三角函数的计算(1)
图片预览




文档简介
课件20张PPT。 .3.三角函数的有关计算(1)
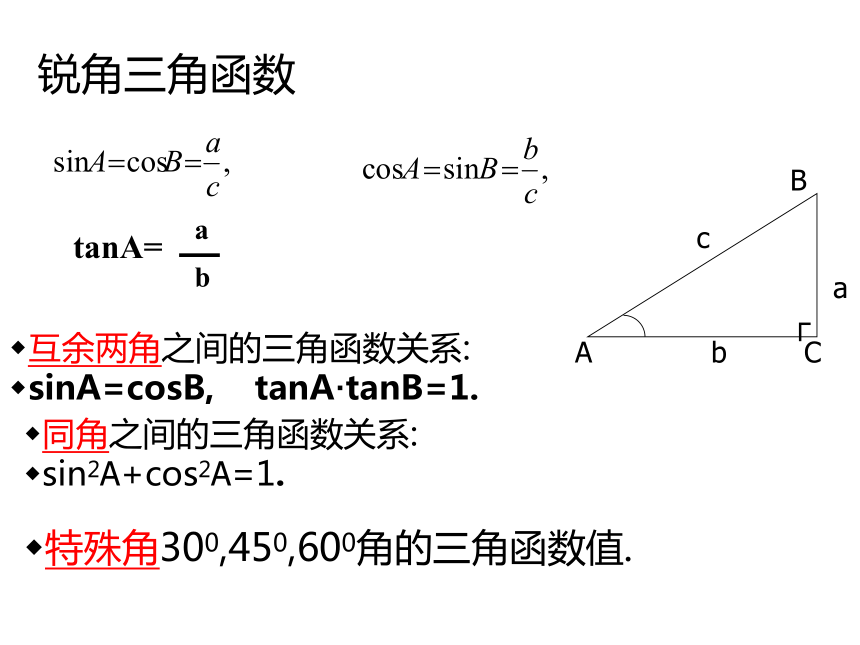
由角求三角函数值互余两角之间的三角函数关系:
sinA=cosB, tanA·tanB=1.特殊角300,450,600角的三角函数值.锐角三角函数同角之间的三角函数关系:
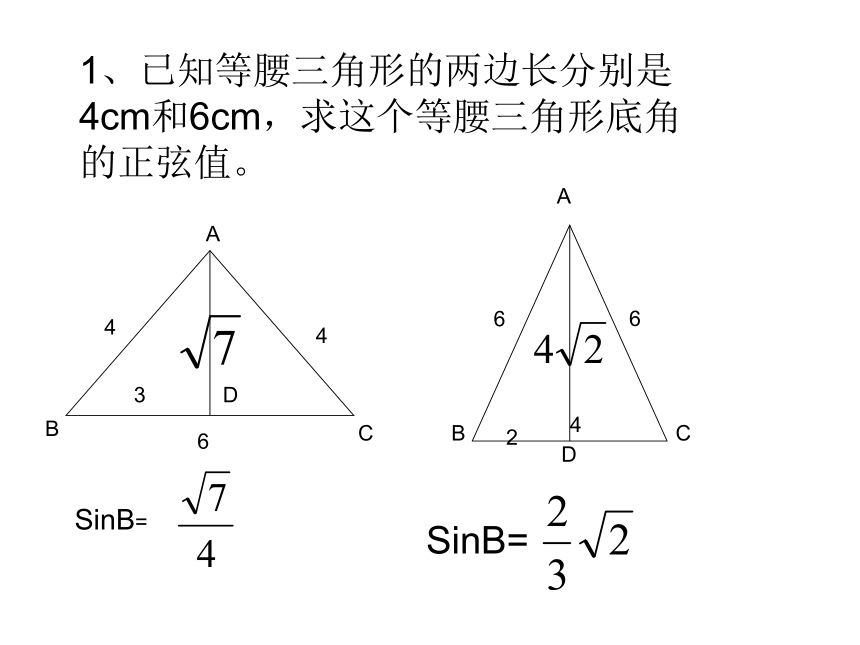
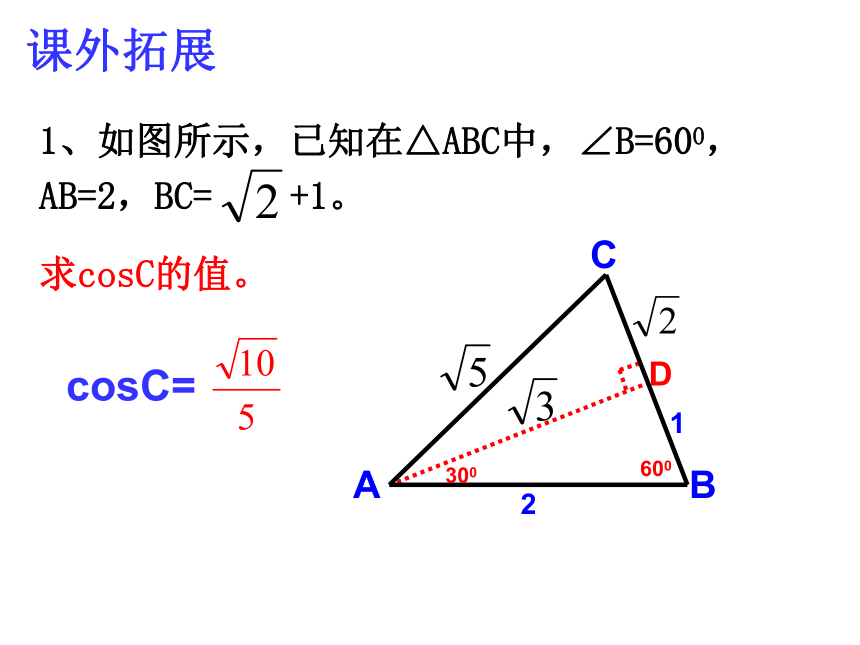
sin2A+cos2A=1.tanA=1、已知等腰三角形的两边长分别是4cm和6cm,求这个等腰三角形底角的正弦值。D3SinB=D42SinB=课外拓展1、如图所示,已知在△ABC中,∠B=600,AB=2,BC= +1。
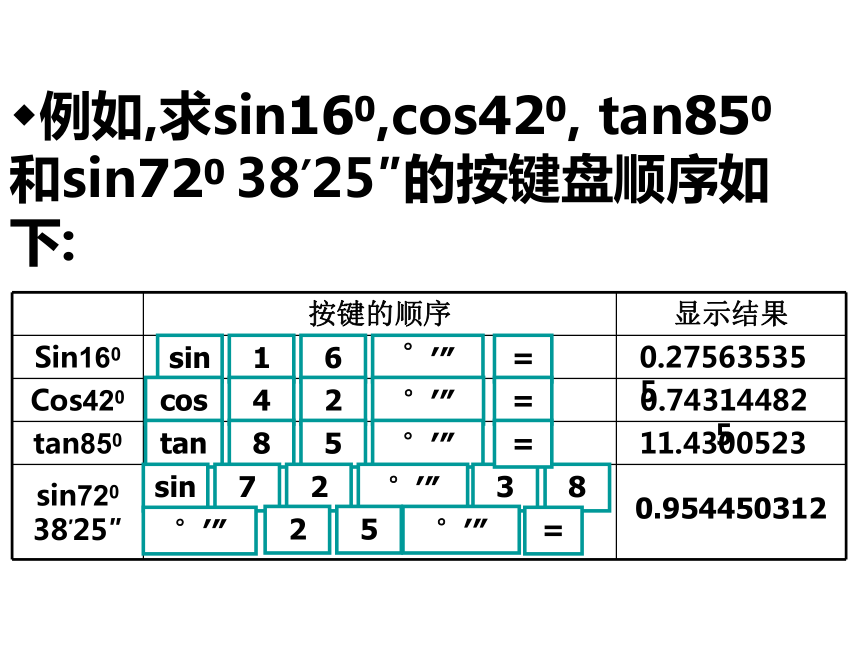
求cosC的值。D60030021cosC=课外拓展2、求证:对于任何锐角α, =tanα用科学计算器求锐角的三角函数值,要用到三个键: 例如,求sin160,cos420, tan850和sin720 38′25″的按键盘顺序如下:例如,求sin160,cos420, tan850和sin720 38′25″的按键盘顺序如下:sin16°′″0.275635355cos42°′″0.743144825tan85°′″11.4300523sin72°′″38°′″25°′″0.954450312====例1;在Rt△ABC中, ∠C =90 ° 。已知AB=12cm, ∠ A=35 ° ,求的周长和面积(周长精确到0.1cm,面积保留3个有效数字).ABCA1 用计算器求下列各式的值:
(1)sin29.120,(2) sin15049′,
(3)cos200,(4)tan290,
(5)tan44059′59″,
(6)sin150+cos610+tan760.随堂练习2. 计算下列各式的值:(1)sin250+cos650
(2) sin360. cos720
(3) tan560. tan340如图,当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角为∠α=160,那么缆车垂直上升的距离是多少?你知道sin160等于多少吗?怎样用科学计算器求锐角的三角函数值呢?如图,在Rt△ABC中,∠C=90°,BC=ABsin16° .对于不是30,45,60这些特殊角的三角函数值, 可以利用计算器来求对于本节一开始提出的问题,利用科学计算器可以求得: BC=ABsin160 ≈200×0.2756≈55.12.1 一个人由山底爬到山顶,需先爬400的山坡300m,再爬300 的山坡100m,求山高(结果精确到0.01m).2.求图中避雷针的长度(结果精确到0.01m).随堂练习3 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.4 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.随堂练习回味无穷直角三角形中的边角关系1填表(一式多变,适当选用):2模型:6 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.7 如图,根据图中已知数据,求AD.随堂练习8 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.9 如图,根据图中已知数据,求AD.随堂练习探究活动:探索下列关系式是否成立(00〈α〈900)?
(1) sinα+cos α≤1
(2) sin2α= 2sinα
P16 习题1.4 1,2题1.用计算器求下列各式的值:
(1)tan320;(2)sin24.530;
(3)sin62011′;(4)tan39039′39″.2.如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部仰角是450,而大厦底部的俯角是370,求该大厦的的高度 (结果精确到0.1m).老师提示:当从低处观察高处的目标时.视线与水平线所成的锐角称为仰角.当从高处观察低处的目标时.视线与水平线所成的锐角称为俯角.
由角求三角函数值互余两角之间的三角函数关系:
sinA=cosB, tanA·tanB=1.特殊角300,450,600角的三角函数值.锐角三角函数同角之间的三角函数关系:
sin2A+cos2A=1.tanA=1、已知等腰三角形的两边长分别是4cm和6cm,求这个等腰三角形底角的正弦值。D3SinB=D42SinB=课外拓展1、如图所示,已知在△ABC中,∠B=600,AB=2,BC= +1。
求cosC的值。D60030021cosC=课外拓展2、求证:对于任何锐角α, =tanα用科学计算器求锐角的三角函数值,要用到三个键: 例如,求sin160,cos420, tan850和sin720 38′25″的按键盘顺序如下:例如,求sin160,cos420, tan850和sin720 38′25″的按键盘顺序如下:sin16°′″0.275635355cos42°′″0.743144825tan85°′″11.4300523sin72°′″38°′″25°′″0.954450312====例1;在Rt△ABC中, ∠C =90 ° 。已知AB=12cm, ∠ A=35 ° ,求的周长和面积(周长精确到0.1cm,面积保留3个有效数字).ABCA1 用计算器求下列各式的值:
(1)sin29.120,(2) sin15049′,
(3)cos200,(4)tan290,
(5)tan44059′59″,
(6)sin150+cos610+tan760.随堂练习2. 计算下列各式的值:(1)sin250+cos650
(2) sin360. cos720
(3) tan560. tan340如图,当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角为∠α=160,那么缆车垂直上升的距离是多少?你知道sin160等于多少吗?怎样用科学计算器求锐角的三角函数值呢?如图,在Rt△ABC中,∠C=90°,BC=ABsin16° .对于不是30,45,60这些特殊角的三角函数值, 可以利用计算器来求对于本节一开始提出的问题,利用科学计算器可以求得: BC=ABsin160 ≈200×0.2756≈55.12.1 一个人由山底爬到山顶,需先爬400的山坡300m,再爬300 的山坡100m,求山高(结果精确到0.01m).2.求图中避雷针的长度(结果精确到0.01m).随堂练习3 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.4 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.随堂练习回味无穷直角三角形中的边角关系1填表(一式多变,适当选用):2模型:6 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.7 如图,根据图中已知数据,求AD.随堂练习8 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.9 如图,根据图中已知数据,求AD.随堂练习探究活动:探索下列关系式是否成立(00〈α〈900)?
(1) sinα+cos α≤1
(2) sin2α= 2sinα
P16 习题1.4 1,2题1.用计算器求下列各式的值:
(1)tan320;(2)sin24.530;
(3)sin62011′;(4)tan39039′39″.2.如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部仰角是450,而大厦底部的俯角是370,求该大厦的的高度 (结果精确到0.1m).老师提示:当从低处观察高处的目标时.视线与水平线所成的锐角称为仰角.当从高处观察低处的目标时.视线与水平线所成的锐角称为俯角.
