3.2三角形的内切圆
图片预览


文档简介
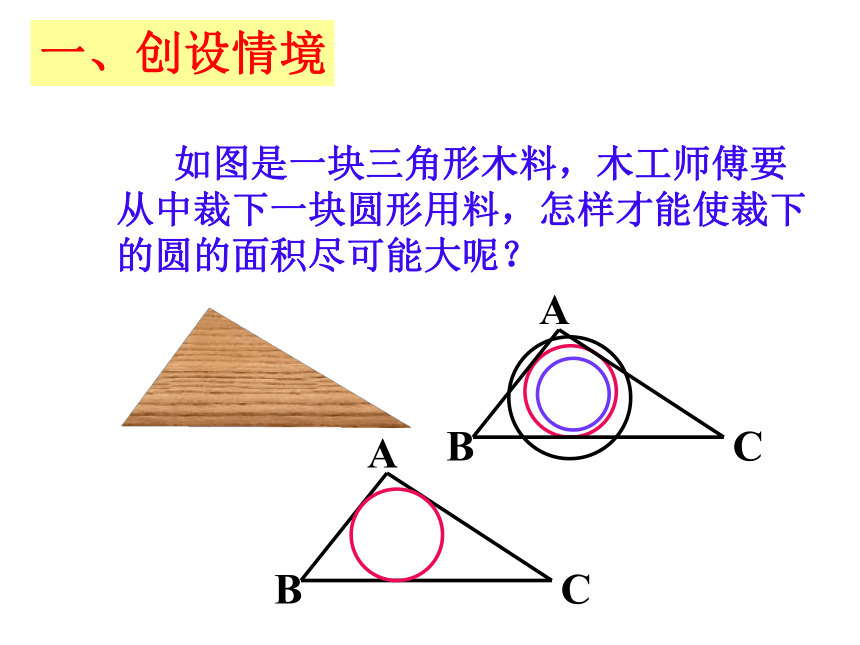
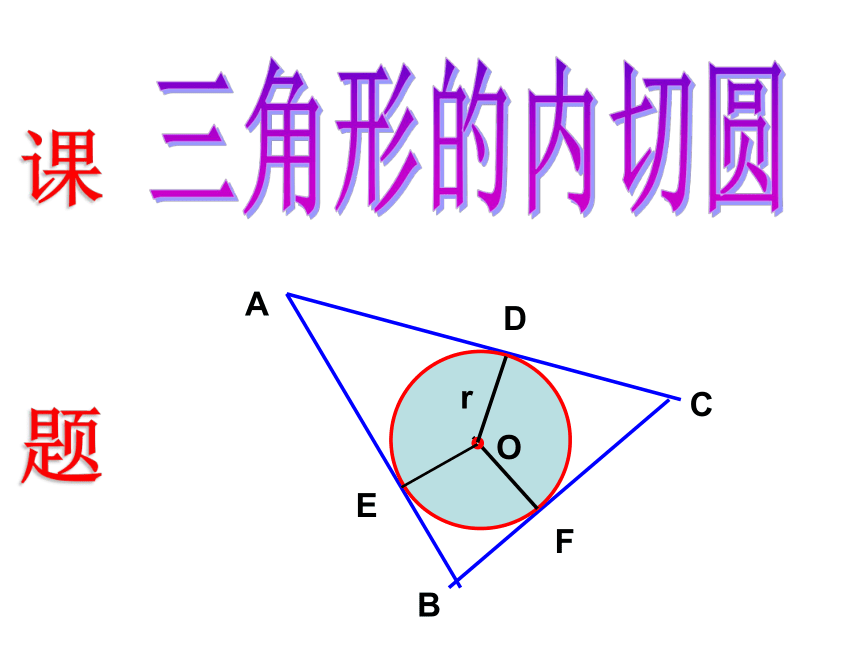
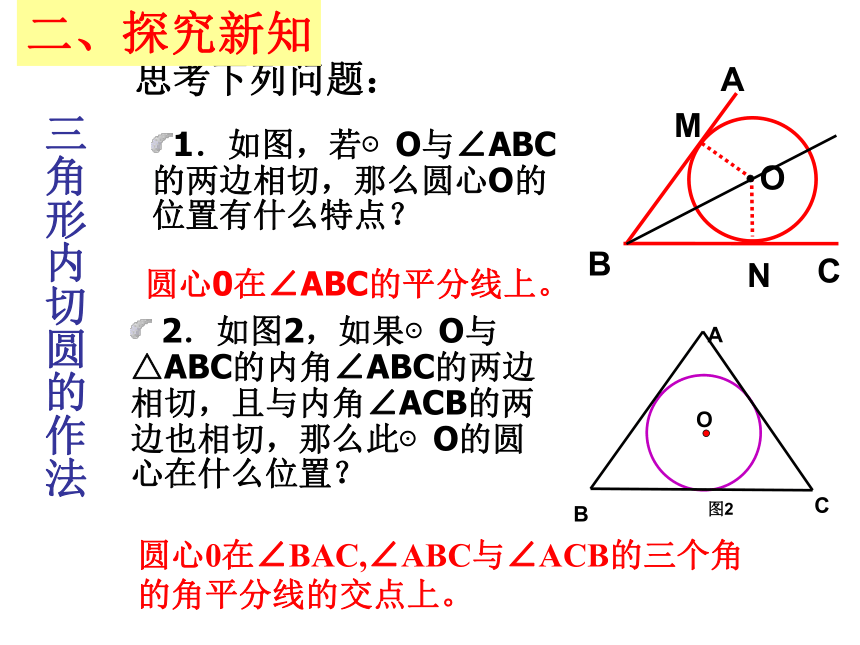
课件26张PPT。三角形的内切圆一、创设情境三角形的内切圆Or课 题思考下列问题:1.如图,若⊙O与∠ABC的两边相切,那么圆心O的位置有什么特点?圆心0在∠ABC的平分线上。?2.如图2,如果⊙O与△ABC的内角∠ABC的两边相切,且与内角∠ACB的两边也相切,那么此⊙O的圆心在什么位置?圆心0在∠BAC,∠ABC与∠ACB的三个角的角平分线的交点上。 OMABCN三角形内切圆的作法二、探究新知3.如何确定一个与三角形
三边都相切的圆的圆心位置
与半径的长? 4.你能作出几个与一个三角形的三边都相切的圆?内切圆圆心能否在三角形外部? 作出三个内角的平分线,三条内角
平分线相交于一点,这点就是符合
条件的圆心,过圆心作一边的垂线,
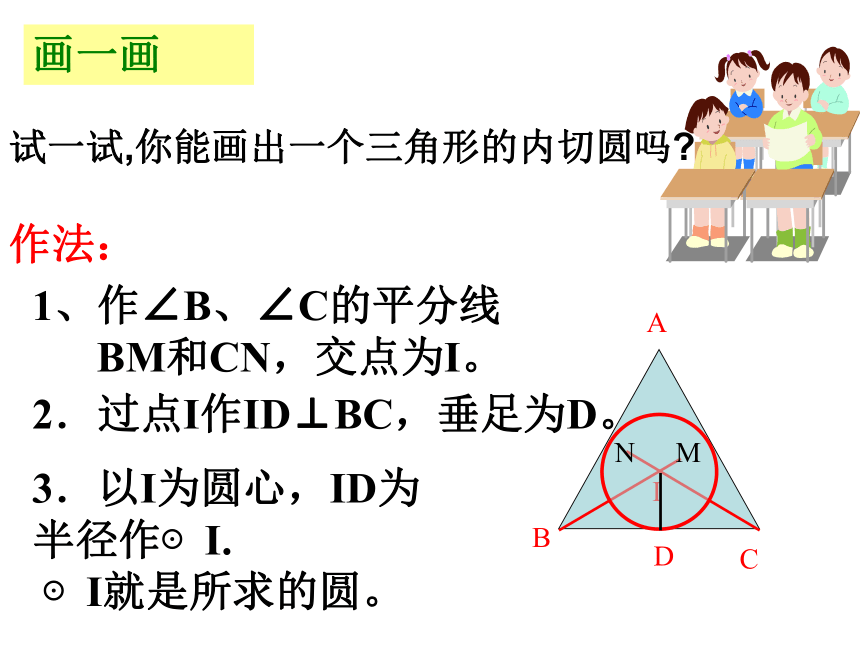
垂线段的长是符合条件的半径。 只能作一个,圆心也只能在三角形内部,因为三角形的三条内角平分线在三角形内部,且只有一个交点。 IFCABED作法: ABC1、作∠B、∠C的平分线
BM和CN,交点为I。 I2.过点I作ID⊥BC,垂足为D。 3.以I为圆心,ID为
半径作⊙I.
⊙I就是所求的圆。 MN试一试,你能画出一个三角形的内切圆吗?
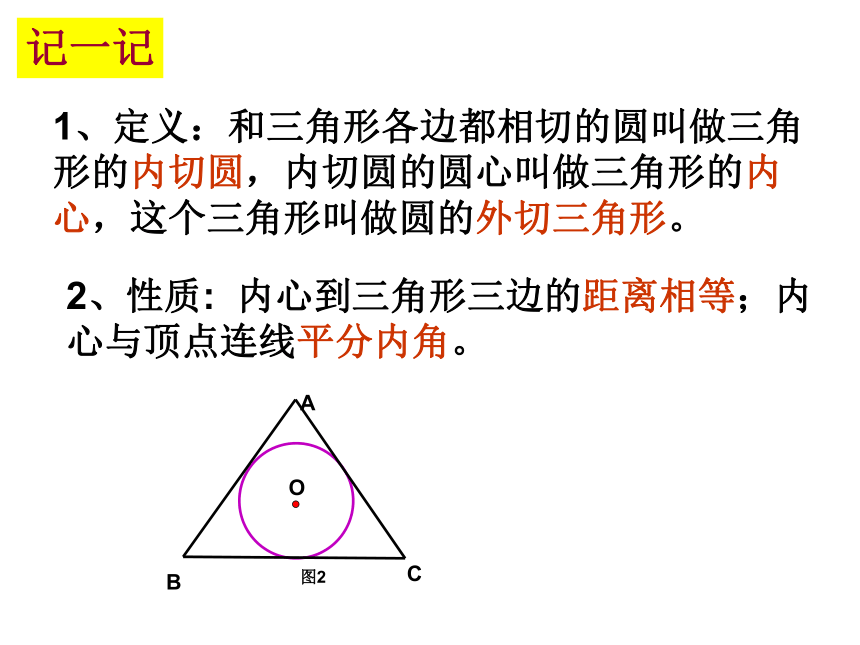
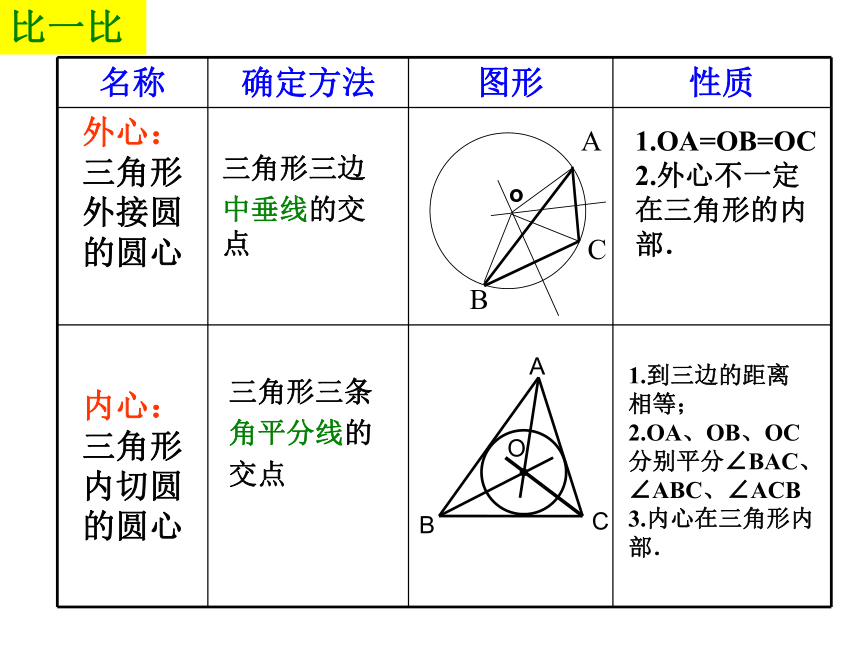
画一画1、定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。2、性质: 内心到三角形三边的距离相等;内心与顶点连线平分内角。记一记三角形三边
中垂线的交点1.OA=OB=OC
2.外心不一定在三角形的内部.三角形三条
角平分线的
交点1.到三边的距离
相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
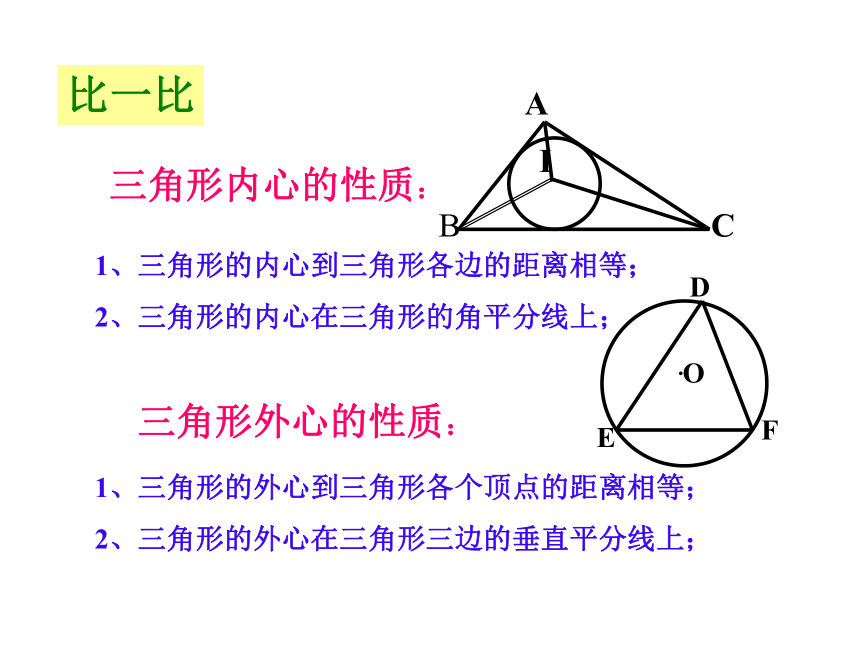
3.内心在三角形内部.oABC比一比三角形内心的性质:1、三角形的内心到三角形各边的距离相等;
2、三角形的内心在三角形的角平分线上; 1、三角形的外心到三角形各个顶点的距离相等;
2、三角形的外心在三角形三边的垂直平分线上; 三角形外心的性质:比一比 1.如图1,△ABC是⊙O的 三角形。⊙ O是△ABC的 圆,
点O叫△ABC的 它是三角形 __________的交点。外接内接外心三边中垂线2.如图2,△DEF是⊙I的 三角形,
⊙I是△DEF的 圆,
点I是 △DEF的 心,
它是三角形 的交点。外切内切内三条角平分线填一填例题1:如图,在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,求∠BOC的
度数。 分析: ∠O = ? ∠1 + ∠3= ? O为△ABC的内心 BO是∠ABC的角平分线 CO是∠ACB的角平分线 三角形内心性质的应用三、例题讲解解: ∵点O为△ABC的内心 ∴∠1=∠2= ∴ ∠BOC=1800 - (∠1+∠2)
=1800 - (250+37.50)
=117.50
∴ ∠BOC=117.50C三角形内心性质的应用整体思想例2、如图,一个木模的上部是圆柱,下部是底面为等边三角形的直三棱柱。圆柱的下底面圆是直三棱柱上底面等边三角形的内切圆,已知直三棱柱的底面等边三角形的边长为3cm,求圆柱底面圆的半径。CABrOD由等边三角形和三角形内切圆的性质可以想到什么?如图是这个木模的俯视图CABrOD例2、如图,一个木模的上部是圆柱,下部是底面为等边三角形的直三棱柱。圆柱的下底面圆是直三棱柱上底面等边三角形的内切圆,已知直三棱柱的底面等边三角形的边长为3cm,求圆柱底面圆的半径。解: 如图是这个木模的俯视图,设圆o切AB于点D,连结OA,
OB,OD.∵⊙o是△ABC的内切圆,∴AO,BO是∠BAC, ∠ABC的角平分线∵ △ABC是等边三角形,∴ ∠OAB=∠OBA=300∵OD⊥AB,AB=3cm,∴AD=BD= AB=1.5(cm)∴OD=AD. tan300= (cm)答:圆柱底面圆的半径为 cm. 五、课内练习
求边长为6cm的等边三角形的内切圆半径r与外接圆半径R。老师提示:
先画草图,由等边三角形一边上的中垂
线与对应顶角平分线重合的性质知,等边三角形的内切圆与外接圆是两个同心圆。若正三角形边长为a,
则内切圆半径r=
外接圆半径R=
sin∠OBD=sin30°=
例3、如图,已知⊙O 是△ABC的内切圆,切点分别点D、E、F,设△ABC周长为L。
求证:AE+BC= L AE=AF BD=BF CD=CE △AFO≌ △AEO (HL)AE+BC=AE+CD+BD= (AE+AF+CD+CE+BD+BF) = (AB+AC+BC)= L 课内练习
设△ABC的面积为S,周长为L, △ABC内切圆
的半径为r,你能
得到S= Lr吗?想想:
要求出三角形的面积
需要哪些量?
根据三角形内心的性质,
可以如何添加辅助线?课内练习题3:请画在课本上.
ABCOcDEr如:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。 变式
如图,直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径r为:
(以含a、b、c的代数式表示r)2cma+b-c=?CD+CE也可用面积得出结论圆内接平行四边形是矩形圆外切平行四边形是_______F菱形EGH四、拓展延伸以某三角形的内心为圆心,作一个圆使它与这个三角形的某一条边(或所在的直线)有两个交点,那么这个圆与其他两边(或所在的直线)有怎样的位置关系?仔细观察图形,你还能发现什么规律?再作几个三角形试一试,是否有同样的规律?请说明理由.OABCFEDGHI六、探究活动我有哪些收获?
---与大家共分享!学 而 不 思 则 罔回头一看,我想说…1.定义2.内心的性质4.初步应用3.画三角形的内切圆七、课后小结八、学以致用1. ) 三角形的内心到三角形各个顶点的距离相等( )
2. ) 三角形的外心到三角形各边的距离相等 ( )
3. ) 等边三角形的内心和外心重合; ( )
4. ) 三角形的内心一定在三角形的内部( )
5. ) 菱形一定有内切圆( )
6. ) 矩形一定有内切圆( )错错对对 错 对1、判断题:九、当堂检测(2)如图,如果AF=2cm,BD=7cm,CE=4cm,则BC= cm,AC= AB= (3)如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )APABD十、布置作业:1、必做题:作业本3.2节
2、选做题:教材 P604-5
再见!祝同学们学习进步!
平分线相交于一点,这点就是符合
条件的圆心,过圆心作一边的垂线,
垂线段的长是符合条件的半径。 只能作一个,圆心也只能在三角形内部,因为三角形的三条内角平分线在三角形内部,且只有一个交点。 IFCABED作法: ABC1、作∠B、∠C的平分线
BM和CN,交点为I。 I2.过点I作ID⊥BC,垂足为D。 3.以I为圆心,ID为
半径作⊙I.
⊙I就是所求的圆。 MN试一试,你能画出一个三角形的内切圆吗?
画一画1、定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。2、性质: 内心到三角形三边的距离相等;内心与顶点连线平分内角。记一记三角形三边
中垂线的交点1.OA=OB=OC
2.外心不一定在三角形的内部.三角形三条
角平分线的
交点1.到三边的距离
相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.oABC比一比三角形内心的性质:1、三角形的内心到三角形各边的距离相等;
2、三角形的内心在三角形的角平分线上; 1、三角形的外心到三角形各个顶点的距离相等;
2、三角形的外心在三角形三边的垂直平分线上; 三角形外心的性质:比一比 1.如图1,△ABC是⊙O的 三角形。⊙ O是△ABC的 圆,
点O叫△ABC的 它是三角形 __________的交点。外接内接外心三边中垂线2.如图2,△DEF是⊙I的 三角形,
⊙I是△DEF的 圆,
点I是 △DEF的 心,
它是三角形 的交点。外切内切内三条角平分线填一填例题1:如图,在△ABC中,∠ABC=50°,∠ACB=75°,点O是内心,求∠BOC的
度数。 分析: ∠O = ? ∠1 + ∠3= ? O为△ABC的内心 BO是∠ABC的角平分线 CO是∠ACB的角平分线 三角形内心性质的应用三、例题讲解解: ∵点O为△ABC的内心 ∴∠1=∠2= ∴ ∠BOC=1800 - (∠1+∠2)
=1800 - (250+37.50)
=117.50
∴ ∠BOC=117.50C三角形内心性质的应用整体思想例2、如图,一个木模的上部是圆柱,下部是底面为等边三角形的直三棱柱。圆柱的下底面圆是直三棱柱上底面等边三角形的内切圆,已知直三棱柱的底面等边三角形的边长为3cm,求圆柱底面圆的半径。CABrOD由等边三角形和三角形内切圆的性质可以想到什么?如图是这个木模的俯视图CABrOD例2、如图,一个木模的上部是圆柱,下部是底面为等边三角形的直三棱柱。圆柱的下底面圆是直三棱柱上底面等边三角形的内切圆,已知直三棱柱的底面等边三角形的边长为3cm,求圆柱底面圆的半径。解: 如图是这个木模的俯视图,设圆o切AB于点D,连结OA,
OB,OD.∵⊙o是△ABC的内切圆,∴AO,BO是∠BAC, ∠ABC的角平分线∵ △ABC是等边三角形,∴ ∠OAB=∠OBA=300∵OD⊥AB,AB=3cm,∴AD=BD= AB=1.5(cm)∴OD=AD. tan300= (cm)答:圆柱底面圆的半径为 cm. 五、课内练习
求边长为6cm的等边三角形的内切圆半径r与外接圆半径R。老师提示:
先画草图,由等边三角形一边上的中垂
线与对应顶角平分线重合的性质知,等边三角形的内切圆与外接圆是两个同心圆。若正三角形边长为a,
则内切圆半径r=
外接圆半径R=
sin∠OBD=sin30°=
例3、如图,已知⊙O 是△ABC的内切圆,切点分别点D、E、F,设△ABC周长为L。
求证:AE+BC= L AE=AF BD=BF CD=CE △AFO≌ △AEO (HL)AE+BC=AE+CD+BD= (AE+AF+CD+CE+BD+BF) = (AB+AC+BC)= L 课内练习
设△ABC的面积为S,周长为L, △ABC内切圆
的半径为r,你能
得到S= Lr吗?想想:
要求出三角形的面积
需要哪些量?
根据三角形内心的性质,
可以如何添加辅助线?课内练习题3:请画在课本上.
ABCOcDEr如:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。 变式
如图,直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径r为:
(以含a、b、c的代数式表示r)2cma+b-c=?CD+CE也可用面积得出结论圆内接平行四边形是矩形圆外切平行四边形是_______F菱形EGH四、拓展延伸以某三角形的内心为圆心,作一个圆使它与这个三角形的某一条边(或所在的直线)有两个交点,那么这个圆与其他两边(或所在的直线)有怎样的位置关系?仔细观察图形,你还能发现什么规律?再作几个三角形试一试,是否有同样的规律?请说明理由.OABCFEDGHI六、探究活动我有哪些收获?
---与大家共分享!学 而 不 思 则 罔回头一看,我想说…1.定义2.内心的性质4.初步应用3.画三角形的内切圆七、课后小结八、学以致用1. ) 三角形的内心到三角形各个顶点的距离相等( )
2. ) 三角形的外心到三角形各边的距离相等 ( )
3. ) 等边三角形的内心和外心重合; ( )
4. ) 三角形的内心一定在三角形的内部( )
5. ) 菱形一定有内切圆( )
6. ) 矩形一定有内切圆( )错错对对 错 对1、判断题:九、当堂检测(2)如图,如果AF=2cm,BD=7cm,CE=4cm,则BC= cm,AC= AB= (3)如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )APABD十、布置作业:1、必做题:作业本3.2节
2、选做题:教材 P604-5
再见!祝同学们学习进步!
