三角形的内切圆复习
图片预览

文档简介
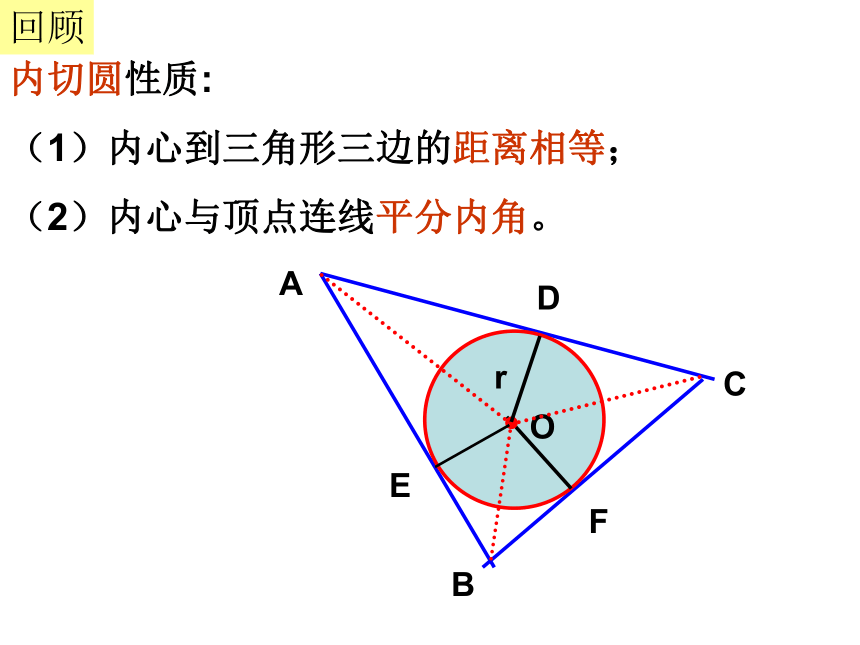
课件13张PPT。回顾内切圆性质:
(1)内心到三角形三边的距离相等;
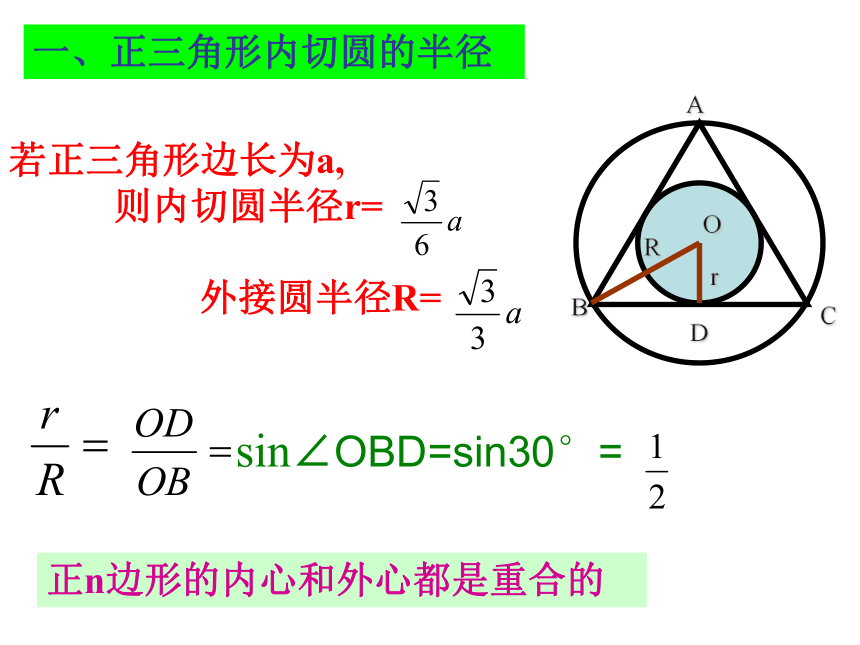
(2)内心与顶点连线平分内角。Or若正三角形边长为a,
则内切圆半径r=
外接圆半径R=
sin∠OBD=sin30°=
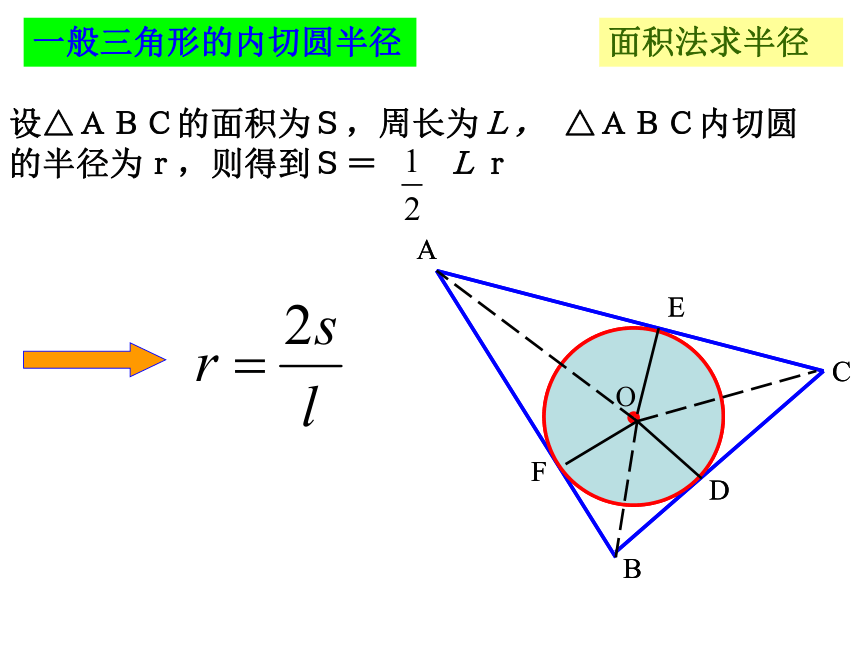
一、正三角形内切圆的半径正n边形的内心和外心都是重合的设△ABC的面积为S,周长为L, △ABC内切圆
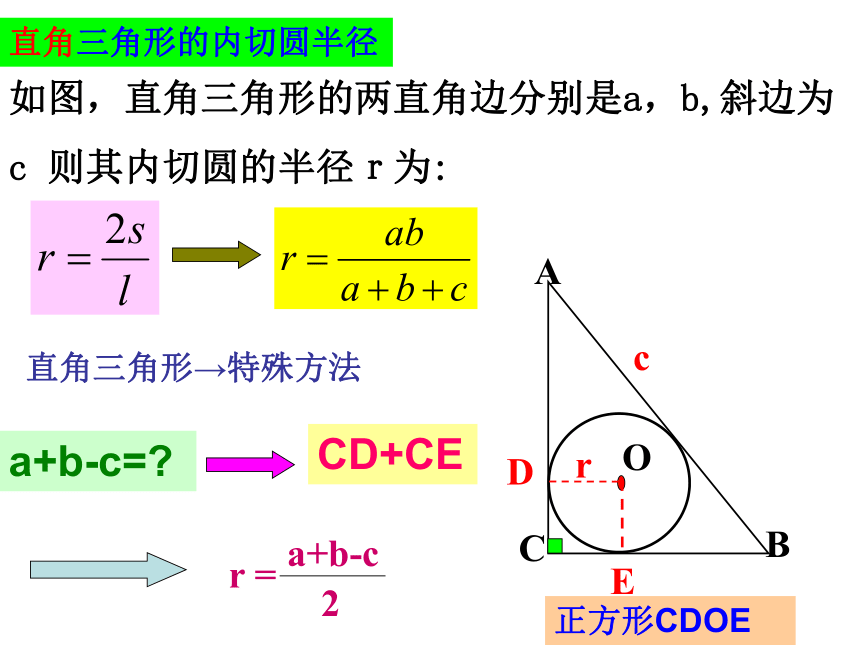
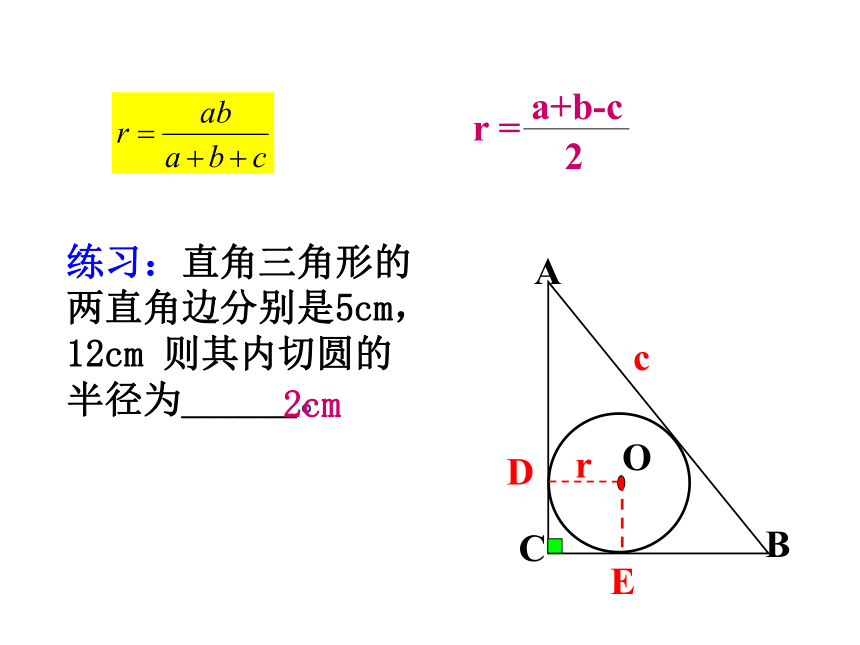
的半径为r,则得到S= Lr面积法求半径一般三角形的内切圆半径ABCOcDEr如图,直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径r为:a+b-c=?CD+CE直角三角形的内切圆半径直角三角形→特殊方法正方形CDOEABCOcDEr练习:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。2cm以某三角形的内心为圆心,作一个圆使它与这个三角形的某一条边(或所在的直线)有两个交点,那么这个圆与其他两边(或所在的直线)有怎样的位置关系?仔细观察图形,你还能发现什么规律?再作几个三角形试一试,是否有同样的规律?请说明理由.OABCFEDGHI探究活动如图,在半径为R的圆内作一个内接正方形,然后
作这个正方形的内切圆,又在这个内切圆中作内接
正方形,依此作到第n个内切圆,它的半径是( )A.B.C.D.思考题8.如图,⊙O为△ABC的内切圆,∠C=90°,AO的延长
线交BC于点D,AC=6,DC=2,则⊙O的半径等于( )
B.2 C.1.5D.2.5A.1.5 C EF知识回顾1.切线的性质:经过切点的半径垂直于圆的切线经过切点垂直于切线的直线必经过圆心2.切线性质的应用:常用的辅助线是连接半径.综合性较强,要联系许多其它图形的性质.ACBAODE弦切角
切线与弦所夹的角叫弦切角,它的度数等于所夹弧的度数,等于所夹弧所对圆心角度数的一半,等于所夹弧所对的圆周角的度数.P=∠P4、如图:PA,PC分别切圆O于点A,C两点,B为圆O上与A,C不重合的点,若∠P=50°,求∠ABC的度数。练一练7、如图,∠P=50°,PA、PC、DE都为⊙O的切线,则∠DOE为 。 变式:改变切线DE的位置,则∠DOE= ;F65°65°归纳:只要∠P的大小不变,∠DOE也不变.练一练如图:已知PA,PB分别切⊙O于A,B两点,如果∠P=60° ,PA=2,那么AB的长为_____.2变式1: CD也与⊙O相切,切点为E.交PA于C点,交PB于D点,则△PCD的周长为____.4变式2: 改变切点E的位置(在劣弧AB上),则△ PCD的周长为 .变式3:若PA=5则△PCD的周长为____.410变式4:若PA=a,则△PCD的周长为 .2a做一做=PC+CD+PD=PC+CE+DE+PD=PC+CA+DB+PD=PA+PB周长
(1)内心到三角形三边的距离相等;
(2)内心与顶点连线平分内角。Or若正三角形边长为a,
则内切圆半径r=
外接圆半径R=
sin∠OBD=sin30°=
一、正三角形内切圆的半径正n边形的内心和外心都是重合的设△ABC的面积为S,周长为L, △ABC内切圆
的半径为r,则得到S= Lr面积法求半径一般三角形的内切圆半径ABCOcDEr如图,直角三角形的两直角边分别是a,b,斜边为c 则其内切圆的半径r为:a+b-c=?CD+CE直角三角形的内切圆半径直角三角形→特殊方法正方形CDOEABCOcDEr练习:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。2cm以某三角形的内心为圆心,作一个圆使它与这个三角形的某一条边(或所在的直线)有两个交点,那么这个圆与其他两边(或所在的直线)有怎样的位置关系?仔细观察图形,你还能发现什么规律?再作几个三角形试一试,是否有同样的规律?请说明理由.OABCFEDGHI探究活动如图,在半径为R的圆内作一个内接正方形,然后
作这个正方形的内切圆,又在这个内切圆中作内接
正方形,依此作到第n个内切圆,它的半径是( )A.B.C.D.思考题8.如图,⊙O为△ABC的内切圆,∠C=90°,AO的延长
线交BC于点D,AC=6,DC=2,则⊙O的半径等于( )
B.2 C.1.5D.2.5A.1.5 C EF知识回顾1.切线的性质:经过切点的半径垂直于圆的切线经过切点垂直于切线的直线必经过圆心2.切线性质的应用:常用的辅助线是连接半径.综合性较强,要联系许多其它图形的性质.ACBAODE弦切角
切线与弦所夹的角叫弦切角,它的度数等于所夹弧的度数,等于所夹弧所对圆心角度数的一半,等于所夹弧所对的圆周角的度数.P=∠P4、如图:PA,PC分别切圆O于点A,C两点,B为圆O上与A,C不重合的点,若∠P=50°,求∠ABC的度数。练一练7、如图,∠P=50°,PA、PC、DE都为⊙O的切线,则∠DOE为 。 变式:改变切线DE的位置,则∠DOE= ;F65°65°归纳:只要∠P的大小不变,∠DOE也不变.练一练如图:已知PA,PB分别切⊙O于A,B两点,如果∠P=60° ,PA=2,那么AB的长为_____.2变式1: CD也与⊙O相切,切点为E.交PA于C点,交PB于D点,则△PCD的周长为____.4变式2: 改变切点E的位置(在劣弧AB上),则△ PCD的周长为 .变式3:若PA=5则△PCD的周长为____.410变式4:若PA=a,则△PCD的周长为 .2a做一做=PC+CD+PD=PC+CE+DE+PD=PC+CA+DB+PD=PA+PB周长
