浙教版九年级数学上册2.2《简单事件的概率(2)》教学课件 (共24张PPT)
文档属性
| 名称 | 浙教版九年级数学上册2.2《简单事件的概率(2)》教学课件 (共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 849.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-04 00:00:00 | ||
图片预览






文档简介
课件24张PPT。2.2 简单事件的概率(2)必然事件;
在一定条件下必然发生的事件.
不可能事件;
在一定条件下不可能发生的事件.
随机事件;
在一定条件下可能发生也可能不发生的事件.1. 事件可以分成哪几类?如何分别?回顾探究2. 概率的定义 事件A发生的频率m/n接近于某个常数,这时就把这个常数叫做事件A的概率,记作P(A). 0≤P(A) ≤1.
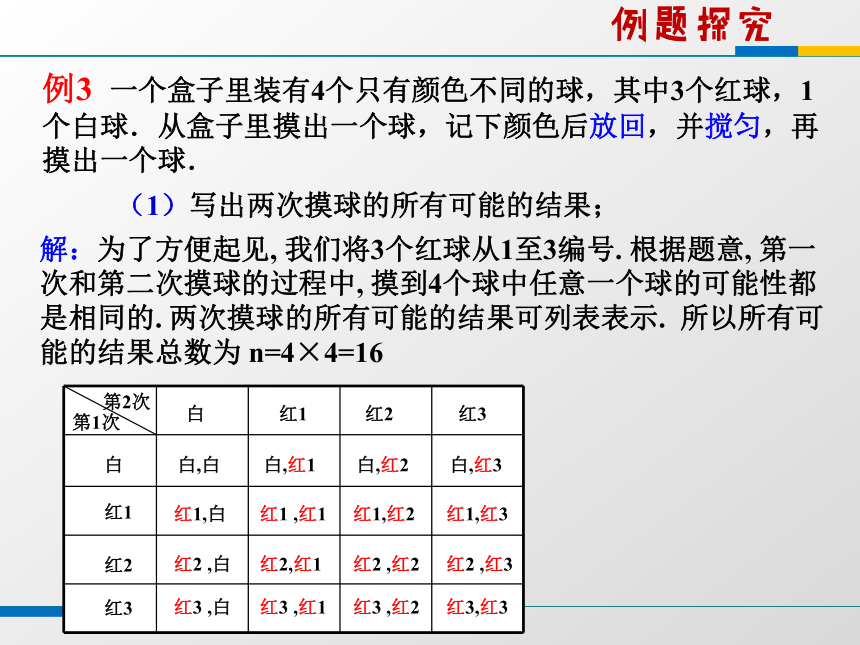
必然事件的概率是1,不可能事件的概率是0.3. 在数学中,我们把事件发生的可能性的大小称为事件发生的概率. 如果事件发生的各种结果的可能性相同, 结果总数为n,其中事件A发生的可能的结果总数为m (m≤n),那么事件A发生的概率:解:为了方便起见, 我们将3个红球从1至3编号. 根据题意, 第一次和第二次摸球的过程中, 摸到4个球中任意一个球的可能性都是相同的. 两次摸球的所有可能的结果可列表表示. 所以所有可能的结果总数为 n=4×4=16 例3 一个盒子里装有4个只有颜色不同的球,其中3个红球,1个白球.从盒子里摸出一个球,记下颜色后放回,并搅匀,再摸出一个球.第1次第2次(1)写出两次摸球的所有可能的结果;例题探究 (2)事件A: “摸出一个红球,一个白球”的概率;第1次第2次解:事件A发生的可能的结果种数m=6
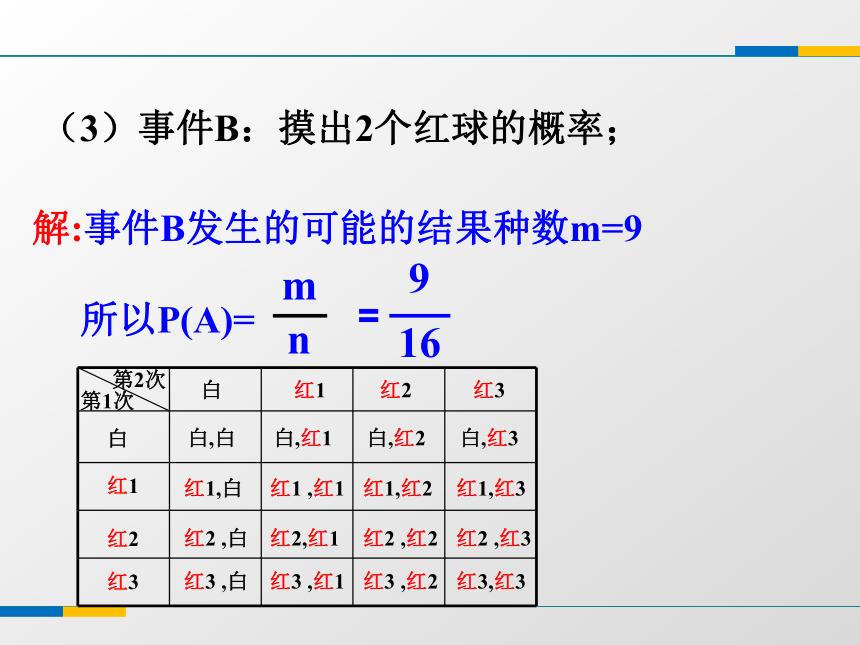
所以P(A)===(3)事件B:摸出2个红球的概率;第1次第2次解:事件B发生的可能的结果种数m=9
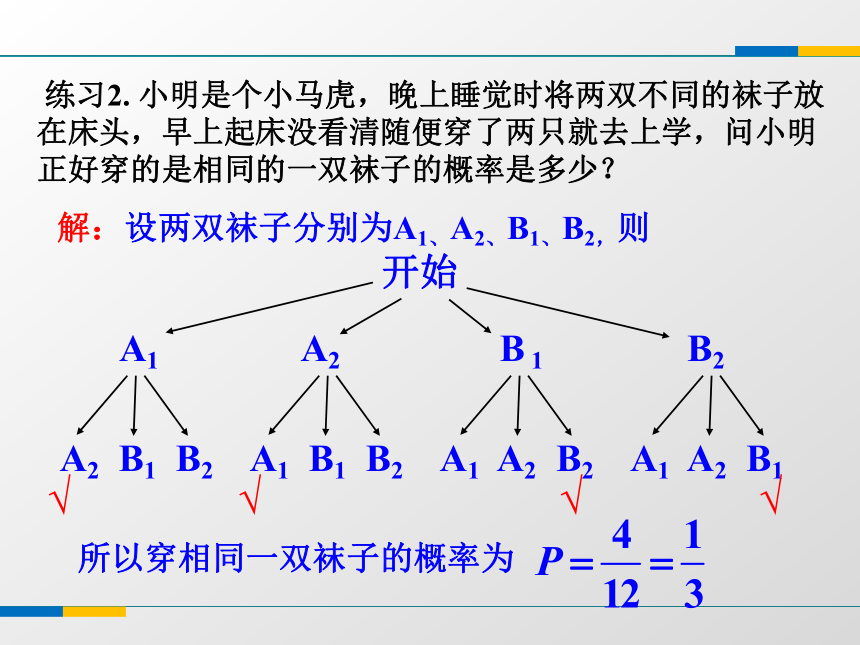
所以P(A)==黄练习1.在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个红色球、两个黄色球.如果第一次先从袋中摸出一个球后不再放回,第二次再从袋中摸出一个,那么两次都摸到黄色球的概率是 _____.开始红黄黄(红,黄)黄红黄红(黄,黄)(黄,红)(黄,黄)(黄,红)黄(红,黄)小试身手 练习2. 小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少?解:设两双袜子分别为A1、A2、B1、B2,则A1 A2 B 1 B2A2 B1 B2 A1 B1 B2 A1 A2 B2 A1 A2 B1所以穿相同一双袜子的概率为第一次所选袜子第二次所选袜子所有可能结果A1A2B1B2A1A2B1B2(A1,A2)(A1,B1)(A1,B2)(A2,A1)(A2,B1)(A2,B2)(B1,A1)(B1,A2)(B1,B2)(B2,A1)(B2,A2)(B2,B1)用表格求所有可能结果时,你可要特别谨慎哦例4.学校组织春游,安排给九年级3辆车,小明与小慧都可以从这3辆车中任选一辆搭乘.问小明与小慧同车的概率有多大?用列表法也试试吧! 你能用树状图表示本题中事件发生的不同结果吗?甲
乙
丙甲
乙
丙甲
乙
丙甲
乙
丙小明
选的车小慧
选的车解:记这三辆车分别为甲、乙、丙,小明与小慧乘车的所有可能的结果列表如下:(各种结果发生的可能性相同)∴所有可能的结果总数为n=9,小明与小慧同车的结果总数为m=33
9∴ P =甲,甲乙,乙丙,丙例5.如图,转盘的白色扇形和红色扇形的圆心角分别为120°和240°.让转盘自由转动2次,求指针一次落在白色区域,另一次落在红色区域的概率. 解:把红色扇形划分成两个圆心角都是120°的扇形(如图)分别为红Ⅰ,红Ⅱ.让转盘自由转动2次,所有可能的结果如图所示,且各种结果发生的可能性相同.∴ 所有可能的结果总数为n=3×3=9,指针一次落在白色区域,另一次落在红色区域的结果总数为m=4.练习3:已知四条线段的长分别是4cm, 5cm, 6cm, 9cm,则从中任意取三条能构成一个三角形的概率是多少?解:从4条线段中任意取3条,共有4种可能(4,5,6),(4,5,9), (4,6,9), (5,6,9), 其中能构成三角形的有3种,因此P(能构成三角形)=3
41、袋子里装有红、黄、蓝三种小球,其形状、大小、质量、质地等完全相同,每种颜色的小球5个,且分别标有数字1,2,3,4,5现从中摸出一球:
(1)摸出的球是蓝色球的概率为多少?
(2)摸出的球是5号球的概率为多少?
(3)摸出的球是红色1号球的概率为多少? 课堂练习2、如图是一个转盘,分成7个相同的扇形,颜色分为红、绿、黄三种颜色,指针的位置固定,转动转盘后任其自由停止.其中的某个扇形会恰好停在指针的位置(如果指针指向两扇形交线时,当作指向右边的扇形),求下列事件的概率:(1) 指针指向红色;解:按颜色把7个扇形分别记为:红1,红2,红3,绿1,绿2,黄1,黄2,所有可能结果共7种.
(1)指针指向红色的结果有3个,即红1,红2,红3,
∴P(指向红色)=3/7;解:(2)指针指向红色或黄色的结果有5个,即红1,红2,红3,黄1,黄2,
∴P(指向红色或黄色)=5/7;(2)指针指向红色或黄色;
(3)指针不指向红色.(3)指针不指向红的结果有4个, 即黄1, 黄2, 绿1, 绿2,
∴P(不指向红色)=4/7.3、任意把骰子连续抛掷两次,(3)朝上一面的点数相同的概率.(4)朝上一面的点数都为偶数的概率.(5)两次朝上一面的点数的和为5的概率.(2)朝上一面的点数一次为3,一次为4的概率.(1)写出抛掷后的所有可能的结果.4.小明和小刚正在做掷骰子的游戏.两人各掷一枚子. (1)当两枚骰子的点数之和为奇数时,小刚得1分,否则小明得1分.这个游戏对双方公平吗? 游戏怎样才算公平?每人获胜的概率是多少?(2)当两枚骰子的点数之积为奇数时,小刚得1分,否则小明得1分.这个游戏对双方公平吗?为什么? 如果事件发生的各种可能结果的可能性相同,那么事件A发生的概率为 把事件发生的可能性的大小称为事件发生的概率.结果总数为n,事件A发生的可能的结果总数为m课堂小结用树状图或表格表示概率 1、利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率. 2、根据不同的情况选择恰当的方法表示某个事件 发生的所有可能结果.课后作业完成课本P50课内练习及作业题1/2
在一定条件下必然发生的事件.
不可能事件;
在一定条件下不可能发生的事件.
随机事件;
在一定条件下可能发生也可能不发生的事件.1. 事件可以分成哪几类?如何分别?回顾探究2. 概率的定义 事件A发生的频率m/n接近于某个常数,这时就把这个常数叫做事件A的概率,记作P(A). 0≤P(A) ≤1.
必然事件的概率是1,不可能事件的概率是0.3. 在数学中,我们把事件发生的可能性的大小称为事件发生的概率. 如果事件发生的各种结果的可能性相同, 结果总数为n,其中事件A发生的可能的结果总数为m (m≤n),那么事件A发生的概率:解:为了方便起见, 我们将3个红球从1至3编号. 根据题意, 第一次和第二次摸球的过程中, 摸到4个球中任意一个球的可能性都是相同的. 两次摸球的所有可能的结果可列表表示. 所以所有可能的结果总数为 n=4×4=16 例3 一个盒子里装有4个只有颜色不同的球,其中3个红球,1个白球.从盒子里摸出一个球,记下颜色后放回,并搅匀,再摸出一个球.第1次第2次(1)写出两次摸球的所有可能的结果;例题探究 (2)事件A: “摸出一个红球,一个白球”的概率;第1次第2次解:事件A发生的可能的结果种数m=6
所以P(A)===(3)事件B:摸出2个红球的概率;第1次第2次解:事件B发生的可能的结果种数m=9
所以P(A)==黄练习1.在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个红色球、两个黄色球.如果第一次先从袋中摸出一个球后不再放回,第二次再从袋中摸出一个,那么两次都摸到黄色球的概率是 _____.开始红黄黄(红,黄)黄红黄红(黄,黄)(黄,红)(黄,黄)(黄,红)黄(红,黄)小试身手 练习2. 小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少?解:设两双袜子分别为A1、A2、B1、B2,则A1 A2 B 1 B2A2 B1 B2 A1 B1 B2 A1 A2 B2 A1 A2 B1所以穿相同一双袜子的概率为第一次所选袜子第二次所选袜子所有可能结果A1A2B1B2A1A2B1B2(A1,A2)(A1,B1)(A1,B2)(A2,A1)(A2,B1)(A2,B2)(B1,A1)(B1,A2)(B1,B2)(B2,A1)(B2,A2)(B2,B1)用表格求所有可能结果时,你可要特别谨慎哦例4.学校组织春游,安排给九年级3辆车,小明与小慧都可以从这3辆车中任选一辆搭乘.问小明与小慧同车的概率有多大?用列表法也试试吧! 你能用树状图表示本题中事件发生的不同结果吗?甲
乙
丙甲
乙
丙甲
乙
丙甲
乙
丙小明
选的车小慧
选的车解:记这三辆车分别为甲、乙、丙,小明与小慧乘车的所有可能的结果列表如下:(各种结果发生的可能性相同)∴所有可能的结果总数为n=9,小明与小慧同车的结果总数为m=33
9∴ P =甲,甲乙,乙丙,丙例5.如图,转盘的白色扇形和红色扇形的圆心角分别为120°和240°.让转盘自由转动2次,求指针一次落在白色区域,另一次落在红色区域的概率. 解:把红色扇形划分成两个圆心角都是120°的扇形(如图)分别为红Ⅰ,红Ⅱ.让转盘自由转动2次,所有可能的结果如图所示,且各种结果发生的可能性相同.∴ 所有可能的结果总数为n=3×3=9,指针一次落在白色区域,另一次落在红色区域的结果总数为m=4.练习3:已知四条线段的长分别是4cm, 5cm, 6cm, 9cm,则从中任意取三条能构成一个三角形的概率是多少?解:从4条线段中任意取3条,共有4种可能(4,5,6),(4,5,9), (4,6,9), (5,6,9), 其中能构成三角形的有3种,因此P(能构成三角形)=3
41、袋子里装有红、黄、蓝三种小球,其形状、大小、质量、质地等完全相同,每种颜色的小球5个,且分别标有数字1,2,3,4,5现从中摸出一球:
(1)摸出的球是蓝色球的概率为多少?
(2)摸出的球是5号球的概率为多少?
(3)摸出的球是红色1号球的概率为多少? 课堂练习2、如图是一个转盘,分成7个相同的扇形,颜色分为红、绿、黄三种颜色,指针的位置固定,转动转盘后任其自由停止.其中的某个扇形会恰好停在指针的位置(如果指针指向两扇形交线时,当作指向右边的扇形),求下列事件的概率:(1) 指针指向红色;解:按颜色把7个扇形分别记为:红1,红2,红3,绿1,绿2,黄1,黄2,所有可能结果共7种.
(1)指针指向红色的结果有3个,即红1,红2,红3,
∴P(指向红色)=3/7;解:(2)指针指向红色或黄色的结果有5个,即红1,红2,红3,黄1,黄2,
∴P(指向红色或黄色)=5/7;(2)指针指向红色或黄色;
(3)指针不指向红色.(3)指针不指向红的结果有4个, 即黄1, 黄2, 绿1, 绿2,
∴P(不指向红色)=4/7.3、任意把骰子连续抛掷两次,(3)朝上一面的点数相同的概率.(4)朝上一面的点数都为偶数的概率.(5)两次朝上一面的点数的和为5的概率.(2)朝上一面的点数一次为3,一次为4的概率.(1)写出抛掷后的所有可能的结果.4.小明和小刚正在做掷骰子的游戏.两人各掷一枚子. (1)当两枚骰子的点数之和为奇数时,小刚得1分,否则小明得1分.这个游戏对双方公平吗? 游戏怎样才算公平?每人获胜的概率是多少?(2)当两枚骰子的点数之积为奇数时,小刚得1分,否则小明得1分.这个游戏对双方公平吗?为什么? 如果事件发生的各种可能结果的可能性相同,那么事件A发生的概率为 把事件发生的可能性的大小称为事件发生的概率.结果总数为n,事件A发生的可能的结果总数为m课堂小结用树状图或表格表示概率 1、利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率. 2、根据不同的情况选择恰当的方法表示某个事件 发生的所有可能结果.课后作业完成课本P50课内练习及作业题1/2
同课章节目录
