浙教版八年级数学上册1.3《证明 》教学课件 (共16张PPT)
文档属性
| 名称 | 浙教版八年级数学上册1.3《证明 》教学课件 (共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 581.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-04 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
1.3 证明(1)
A
B
D
C
线段AB,CD哪条更长?
(1)当n=0时 n2-3n+7=
7
5
5
小明说:“对于自然数n,代数式n2-3n+7的值
都是素数”.
关于代数式n2-3n+7的值的猜测
(2)当n=1时 n2-3n+7=
(3)当n=2时 n2-3n+7=
(1)当n=0时 n2-3n+7=
7
5
5
:“对于自然数n,代数式n2-3n+7的值
都是素数”.
关于代数式n2-3n+7的值的猜测
(2)当n=1时 n2-3n+7=
(3)当n=2时 n2-3n+7=
命题
是真命题吗?
当n=6时 n2-3n+7=25
证明(1)
如图,AC,BD交于点E,AE=CE,BE=DE,
A
B
D
C
E
已知:
则
求证:
吗?请说明理由.
要判定一个命题是真命题,往往需要从
命题的条件出发,根据已知的定义、公理、
定理,一步一步推得结论成立,这样的推理
过程叫做证明.
(2)你还能得到哪些结论?
(1)
∠A=∠C,∠B=∠D,AB=CD,AB∥CD
(3)请选择其中一个结论,
向同桌口述证明过程.
△AEB ≌△CED
△AEB与△CED全等
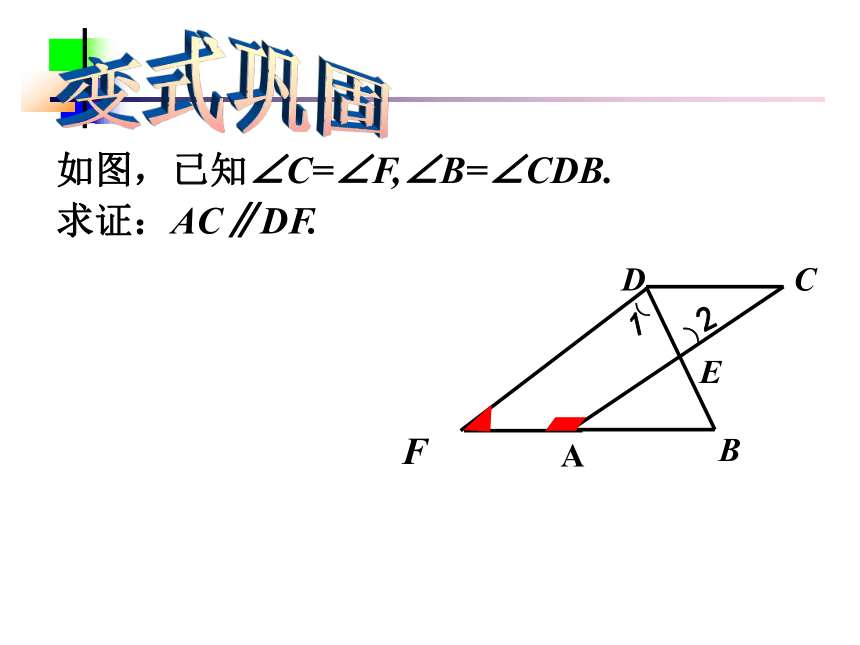
如图,已知∠C=∠F,∠B=∠CDB.
求证:AC∥DF.
A
B
D
C
E
F
⌒
1
⌒
2
一个角的两边分别平行于另一个角的两边,
则这两个角相等 ”
命题 “
是真命题吗?
A
B
C
D
E
F
G
A
B
C
D
E
F
G
A
B
C
D
E
F
A
B
C
D
E
F
G
一个角的两边分别平行于另一个角的两边
则这两个角相等 ”
命题 “
且方向相同,
是真命题
吗?
.
证明
一个角的两边分别平行于另一个角的两边
则这两个角相等 ”
命题 “
且方向相同,
是真命题
.
证明
A
B
C
D
E
F
G
A
B
C
D
E
F
G
线段AB,CD哪条更长?
关于代数式n2-3n+7的值的猜测
感受了证明的必要
如图,AC,BD交于点E,AE=CE,BE=DE,
A
B
D
C
E
已知:
求证:
△AEB ≌△CED
理解了……
学会了……
一个角的两边分别平行于另一个角的两边
则这两个角相等.”
命题:“
且方向相同,
是真命题
.
证明
掌握了……
作业:
1、必做作业:详见学案
2、选做作业:详见学案
1.3 证明(1)
A
B
D
C
线段AB,CD哪条更长?
(1)当n=0时 n2-3n+7=
7
5
5
小明说:“对于自然数n,代数式n2-3n+7的值
都是素数”.
关于代数式n2-3n+7的值的猜测
(2)当n=1时 n2-3n+7=
(3)当n=2时 n2-3n+7=
(1)当n=0时 n2-3n+7=
7
5
5
:“对于自然数n,代数式n2-3n+7的值
都是素数”.
关于代数式n2-3n+7的值的猜测
(2)当n=1时 n2-3n+7=
(3)当n=2时 n2-3n+7=
命题
是真命题吗?
当n=6时 n2-3n+7=25
证明(1)
如图,AC,BD交于点E,AE=CE,BE=DE,
A
B
D
C
E
已知:
则
求证:
吗?请说明理由.
要判定一个命题是真命题,往往需要从
命题的条件出发,根据已知的定义、公理、
定理,一步一步推得结论成立,这样的推理
过程叫做证明.
(2)你还能得到哪些结论?
(1)
∠A=∠C,∠B=∠D,AB=CD,AB∥CD
(3)请选择其中一个结论,
向同桌口述证明过程.
△AEB ≌△CED
△AEB与△CED全等
如图,已知∠C=∠F,∠B=∠CDB.
求证:AC∥DF.
A
B
D
C
E
F
⌒
1
⌒
2
一个角的两边分别平行于另一个角的两边,
则这两个角相等 ”
命题 “
是真命题吗?
A
B
C
D
E
F
G
A
B
C
D
E
F
G
A
B
C
D
E
F
A
B
C
D
E
F
G
一个角的两边分别平行于另一个角的两边
则这两个角相等 ”
命题 “
且方向相同,
是真命题
吗?
.
证明
一个角的两边分别平行于另一个角的两边
则这两个角相等 ”
命题 “
且方向相同,
是真命题
.
证明
A
B
C
D
E
F
G
A
B
C
D
E
F
G
线段AB,CD哪条更长?
关于代数式n2-3n+7的值的猜测
感受了证明的必要
如图,AC,BD交于点E,AE=CE,BE=DE,
A
B
D
C
E
已知:
求证:
△AEB ≌△CED
理解了……
学会了……
一个角的两边分别平行于另一个角的两边
则这两个角相等.”
命题:“
且方向相同,
是真命题
.
证明
掌握了……
作业:
1、必做作业:详见学案
2、选做作业:详见学案
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
