4.2代数式同步练习

4.2代数式同步练习
　
一．选择题（共11小题）
1．火车站、机场、邮局等场所都有为旅客提供打包服务的项目．现有一个长、宽、高分别为a、b、c的箱子，按如图所示的方式打包，则打包带的长（不计接头处的长）至少应为（　　）
A．2a+2b+4c B．2a+4b+6c C．4a+6b+6c D．4a+4b+8c
2．小张在某月的日历上圈出了相邻的三个数a、b、c，并求出了它们的和为33，这三个数在日历中的排布不可能是（　　）
A． B． C． D．
3．一个长方形的周长是30厘米，若长方形的一边用字母x（厘米）表示，则该长方形的面积是（　　）
A．x（30﹣2x）平方厘米 B．x（30﹣x）平方厘米
C．x（15﹣x）平方厘米 D．x（15+x）平方厘米
4．某市举行的青年歌手大奖赛今年共有a人参加，比赛的人数比去年增加20%还多3人，设去年参赛的有x人，则x为（　　）2·1·c·n·j·y
A． B．（1+20%）a+3 C． D．（1+20%）a﹣3
5．负数a和它的相反数的差的绝对值是（　　）
A．2a B．0 C．﹣2a D．±2a
6．某养殖场2013年底的生猪出栏价格是每千克a元，受市场影响，2014年第一季度出栏价格平均每千克下降了15%，到了第二季度平均每千克比第一季度又上升了20%，则第三季度初这家养殖场的生猪出栏价格是每千克（　　）
A．（1﹣15%）（1+20%）a元 B．（1﹣15%）20%a元
C．（1+15%）（1﹣20%）a元 D．（1+20%）15%a元
7．有16m长的木料（宽度不计），要做成一个如图的窗框．假设窗框横档的长度为x m，那么窗框的面积是（　　）
A．x（8﹣x）m2 B．x（16﹣x）m2 C．x（8﹣3x）m2 D．
8．下列说法不正确的是（　　）
A．x的倒数与y的差：﹣y B．x与y的平方的差：x﹣y2
C．x与y的和的倒数： D．x与y和的相反数：﹣x+y
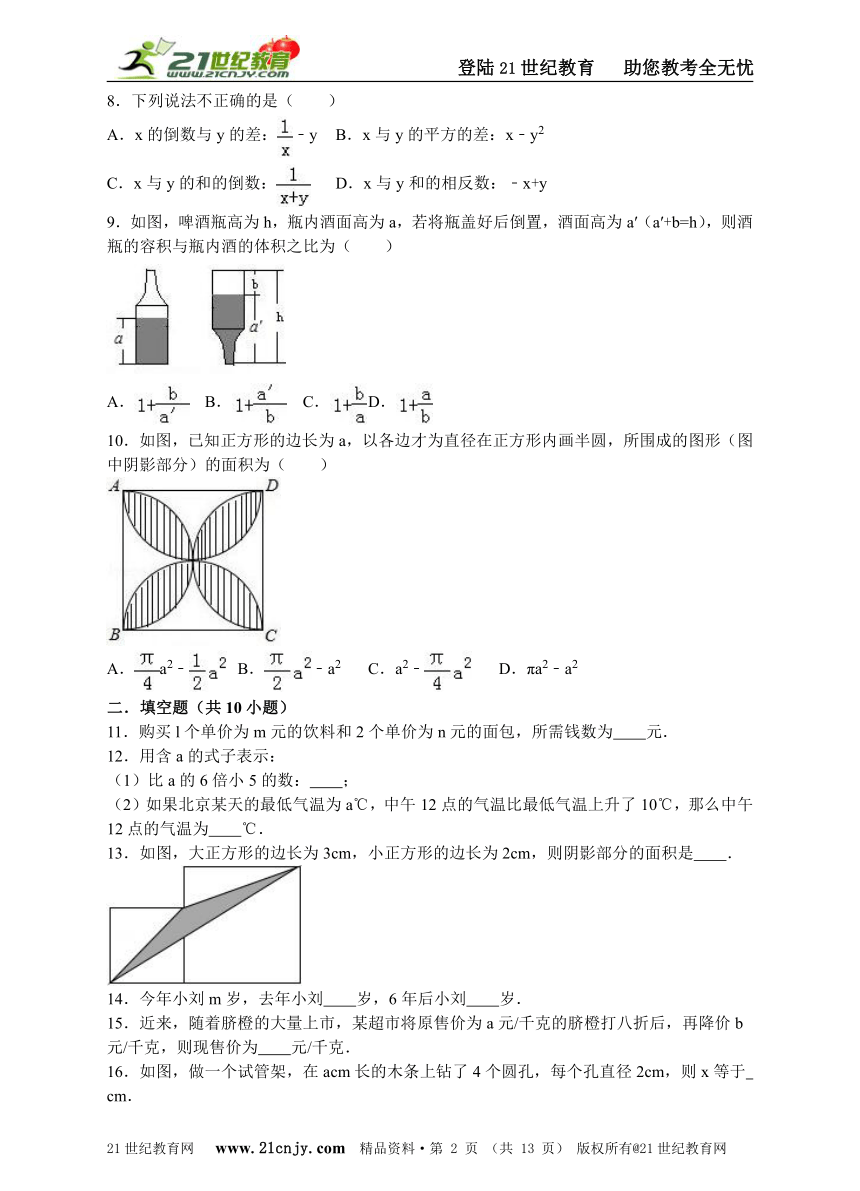
9．如图，啤酒瓶高为h，瓶内酒面高为a，若将瓶盖好后倒置，酒面高为a′（a′+b=h），则酒瓶的容积与瓶内酒的体积之比为（　　）
A． B． C． D．
10．如图，已知正方形的边长为a，以各边才为直径在正方形内画半圆，所围成的图形（图中阴影部分）的面积为（　　）
A．a2﹣ B．﹣a2 C．a2﹣ D．πa2﹣a2　
二．填空题（共10小题）
11．购买l个单价为m元的饮料和2个单价为n元的面包，所需钱数为　　元．
12．用含a的式子表示：
（1）比a的6倍小5的数：　　；
（2）如果北京某天的最低气温为a℃，中午12点的气温比最低气温上升了10℃，那么中午12点的气温为　　℃．
13．如图，大正方形的边长为3cm，小正方形的边长为2cm，则阴影部分的面积是　　．
14．今年小刘m岁，去年小刘　　岁，6年后小刘　　岁．
15．近来，随着脐橙的大量上市，某超市将原售价为a元/千克的脐橙打八折后，再降价b元/千克，则现售价为　　元/千克．
16．如图，做一个试管架，在acm长的木条上钻了4个圆孔，每个孔直径2cm，则x等于　　cm．
17．x表示一个三位数，y表示一个两位数，把三位数x放在两位数y的左边，应该表示为　　．
18．甲、乙两家超市为了促销一种定价相同的商品，甲超市先降价20%，后又降价10%，乙超市连续两次降价15%，那么顾客到　　家超市购买更合算．
19．如图，大正方形的边长为a，小正方形的边长为2，则阴影部分的面积=　　．
20．某商店三月份的销售额为a万元，三月份比二月份减少10%，二月份比一月份增加10%，则一月份的销售额为　　万元．21世纪教育网版权所有
　
三．解答题（共8小题）
21．附加题：观察下面一列数：﹣1，2，﹣3，4，﹣5，6，﹣7，…，将这列数排成如图的形式：
按照上述规律排下去，那么第10行从左边第9个数是　　．
22．甲、乙两人从同一地点出发，甲每小时走6km，乙每小时走4km，用代数式表示：
（1）反向行走t小时后，两人相距多少千米？
（2）同向行走t小时后，两人相距多少千米？
（3）反向行走，甲比乙早出发m小时，则乙走n小时后，两人相距多少千米？
（4）同向行走，甲比乙晚出发m小时，则乙走n小时后（n＞m），两人相距多少千米？
23．某地电话拨号上网有两种收费方式：A计时制：1.5元/时，B包月制：50元/月，此外每种上网方式都要加收通讯费1元/时．www-2-1-cnjy-com
（1）某用户某月上网的时间为x小时，请写出两种收费方式下该用户应该支付的费用；
（2）某用户估计一个月上网的时间为30小时，你认为选择哪种方式合算？
24．窗户的形状如图所示（图中长度单位：cm），其上部是半圆形，下部是边长相同的四个小正方形，已知下部小正方形的边长是a cm，计算：
（1）窗户的面积；
（2）窗户的外框的总长．
25．用代数式表示：
①x，y两数的平方差与这两数和的积是　　；
②x的2倍与x的的和是　　．
26．阅读下面材料，完成相应的填空：
（1）双循环与单循环问题：
小田是个足球迷，他发现有的比赛是单循环的，就是每两个球队之间只赛一场；有的比赛是双循环的，每两个球队按主客场要赛两场，同时小田又是个数学迷，他想探究如果有n（n≥2）个球队进行双循环比赛，一共要赛多少场？
①小田觉得从特殊情况入手可能会找到灵感，于是他取n=2，要赛2场；n=3，赛6场；n=4，赛12场；那么n=5，要赛　　场…，由此得出，n（n≥2）个球队进行双循环比赛，一共要赛　　场．
②聪明的小田由①中的结论，很快地得出n（n≥2）个球队单循环比赛场数为　　；
（2）知识迁移：①平面内有10个点，且任意3个点不在同一条直线上，经过每两点画一条直线，一共能画　　条不同的直线．②一个n边形（n≥3）有　　条对角线．
27．新学期，两摞规格相同的数学课本整齐的叠放在讲台上，请根据图中所给出的数据信息，解答下列问题：
（1）每本书的高度为　　cm，课桌的高度为　　cm；
（2）当课本数为x（本）时，请写出同样叠放在桌面上的一摞数学课本高出地面的距离（用含x的代数式表示）；
（3）桌面上有56本与题（1）中相同的数学课本，整齐叠放成一摞，若从中取走14本，求余下的数学课本高出地面的距离．
　

4.2代数式同步练习
参考答案与试题解析
　
一．选择题（共11小题）
1． 火车站、机场、邮局等场所都有为旅客提供打包服务的项目．现有一个长、宽、高分别为a、b、c的箱子，按如图所示的方式打包，则打包带的长（不计接头处的长）至少应为（　　）
A．2a+2b+4c B．2a+4b+6c C．4a+6b+6c D．4a+4b+8c
解：横向的打包带长是：2a+2c；纵向的打包线长是：2c+2b，
则打包带的总长（不计接头处的长）至少是：2[（2a+2c）+（2c+2b）]=4a+4b+8c．
故选D．
　
2． 小张在某月的日历上圈出了相邻的三个数a、b、c，并求出了它们的和为33，这三个数在日历中的排布不可能是（　　）
A． B． C． D．
解：A、设最小的数是x．x+x+1+x+2=33，x=10．故本选项正确．
B、设最小的数是x．x+x+6+x+7=33，x=，故本选项错误．
C、设最小的数是x．x+x+7+x+8=33，x=6，故本选项正确．
D、设最小的数是x．x+x+7+x+14=33，x=4，本选项正确．
故选B．
　
3． 一个长方形的周长是30厘米，若长方形的一边用字母x（厘米）表示，则该长方形的面积是（　　）
A．x（30﹣2x）平方厘米 B．x（30﹣x）平方厘米
C．x（15﹣x）平方厘米 D．x（15+x）平方厘米
解：∵长方形的周长是30厘米，长方形的一边用为x厘米，
∴长方形的另一边是（15﹣x）厘米，
∴该长方形的面积是x（15﹣x）平方厘米；
故选C．
　
4． 某市举行的青年歌手大奖赛今年共有a人参加，比赛的人数比去年增加20%还多3人，设去年参赛的有x人，则x为（　　）21·世纪*教育网
A． B．（1+20%）a+3 C． D．（1+20%）a﹣3
解：设去年有x人，
∵今年共有a人参加，比赛的人数比去年增加20%还多3人，
∴今年的人数为：x（1+20%）+3=a，
∴x=，
故选C．
　
5． 负数a和它的相反数的差的绝对值是（　　）
A．2a B．0 C．﹣2a D．±2a
解：|a﹣（﹣a）|=|2a|=﹣2a．故选C．
　
6．（2014?日照）某养殖场2013年底的生猪出栏价格是每千克a元，受市场影响，2014年第一季度出栏价格平均每千克下降了15%，到了第二季度平均每千克比第一季度又上升了20%，则第三季度初这家养殖场的生猪出栏价格是每千克（　　）【来源：21·世纪·教育·网】
A．（1﹣15%）（1+20%）a元 B．（1﹣15%）20%a元
C．（1+15%）（1﹣20%）a元 D．（1+20%）15%a元
解：第三季度初这家养殖场的生猪出栏价格是每千克（1﹣15%）（1+20%）a元．
故选：A．
　
7． 有16m长的木料（宽度不计），要做成一个如图的窗框．假设窗框横档的长度为x m，那么窗框的面积是（　　）
A．x（8﹣x）m2 B．x（16﹣x）m2 C．x（8﹣3x）m2 D．
解：结合图形，显然窗框的另一边是=2﹣x（米）．
根据长方形的面积公式，得：窗框的面积是x（2﹣x）平方米．
故选：D．
　
8． 下列说法不正确的是（　　）
A．x的倒数与y的差：﹣y B．x与y的平方的差：x﹣y2
C．x与y的和的倒数： D．x与y和的相反数：﹣x+y
解：A、x的倒数与y的差是﹣y，
B、x与y的平方的差是x﹣y2，
C、x与y的和的倒数是，
D、x与y和的相反数是﹣x﹣y，
故选D．
　
9． 如图，啤酒瓶高为h，瓶内酒面高为a，若将瓶盖好后倒置，酒面高为a′（a′+b=h），则酒瓶的容积与瓶内酒的体积之比为（　　）　　21*cnjy*com
A． B． C． D．
解：设啤酒瓶的底面积为x，酒瓶的容积为1，
ax=1﹣bx，
解得x=，
∴酒的体积为：×a=，
∴酒瓶的容积与瓶内酒的体积之比为：1：=．
故选C．
　
10． 如图，已知正方形的边长为a，以各边才为直径在正方形内画半圆，所围成的图形（图中阴影部分）的面积为（　　）【版权所有：21教育】
A．a2﹣ B．﹣a2 C．a2﹣ D．πa2﹣a2
解：为图中各部分面积表示名称，如图
∵S阴影=S1+S2+S3+S2，
4个半圆的面积是（S1+S2+S3+S4）+（S2+S6+S3）+（S3+S7+S4）+（S1+S8+S4）=（S1+S2+S3+S4）+（S1+S2+S3+S4+S5+S6+S7+S8），【来源：21cnj*y.co*m】
正方形的面积=S1+S2+S3+S4+S5+S6+S7+S8，
∴S阴影=4个半圆的面积﹣正方形的面积，
正方形的边长为a，且a为半圆的直径，
∴S阴影=4×π×﹣a2=a2﹣a2．
故选B．
　

　
二．填空题（共10小题）
11． 购买l个单价为m元的饮料和2个单价为n元的面包，所需钱数为　（m+2n）　元．
解：购买l个单价为m元的饮料和2个单价为n元的面包，所需钱数为：（m+2n）元，
故答案为：（m+2n）．
　
12． 用含a的式子表示：
（1）比a的6倍小5的数：　6a﹣5　；
（2）如果北京某天的最低气温为a℃，中午12点的气温比最低气温上升了10℃，那么中午12点的气温为　（a+10）　℃．www.21-cn-jy.com
解：（1）a的6倍为6a，小5即为6a﹣5；
（2）中午12点的气温为（a+10）℃．
故答案为：6a﹣5；（a+10）．
　
13． 如图，大正方形的边长为3cm，小正方形的边长为2cm，则阴影部分的面积是　2cm2　．
解：由图可知，
阴影部分的面积是：=9+4﹣7.5﹣2﹣1.5=2cm2，
故答案为：2cm2．
　
14． 今年小刘m岁，去年小刘　m﹣1　岁，6年后小刘　m+6　岁．
解：∵今年小刘m岁，
∴去年小刘m﹣1岁，6年后小刘m+6岁．
故答案为：m﹣1，m+6．
　
15． 近来，随着脐橙的大量上市，某超市将原售价为a元/千克的脐橙打八折后，再降价b元/千克，则现售价为　（0.8a﹣b）　元/千克．21教育网
解：第一次降价打“八折”后的价格：80%a=0.8a元，
第二次降价后的价格：（0.8a﹣b）元．
故答案为：（0.8a﹣b）．
　
16． 如图，做一个试管架，在acm长的木条上钻了4个圆孔，每个孔直径2cm，则x等于　　cm．
解：由题意，得
5x+4×2=a，
解得：x=．
故答案为：．
　
17．x表示一个三位数，y表示一个两位数，把三位数x放在两位数y的左边，应该表示为　100x+y　．21·cn·jy·com
解：表示为：100x+y．
故答案是：100x+y．
　
1 8． 甲、乙两家超市为了促销一种定价相同的商品，甲超市先降价20%，后又降价10%，乙超市连续两次降价15%，那么顾客到　甲　家超市购买更合算．
解：由题意可得，设商品的定价为a
甲超市两次降价后为：a×（1﹣20%）×（1﹣10%）=0.72a；
乙超市连续两次降价后为：a×（1﹣15%）×（1﹣15%）=0.7225a．
∵0.72a＜0.7225a，
∴选择甲超市．
故答案为：甲
　
19． 如图，大正方形的边长为a，小正方形的边长为2，则阴影部分的面积=　a　．
解：由图可得，
阴影部分的面积是：=，
故答案为：a．
　
20． 某商店三月份的销售额为a万元，三月份比二月份减少10%，二月份比一月份增加10%，则一月份的销售额为　　万元．2-1-c-n-j-y
解：设一月份的销售额为x，由题意可得，
x（1+10%）（1﹣10%）=a
解得，x=
故答案为．
　
三．解答题（共8小题）
21． 附加题：观察下面一列数：﹣1，2，﹣3，4，﹣5，6，﹣7，…，将这列数排成如图的形式：
按照上述规律排下去，那么第10行从左边第9个数是　90　．
解：9×9=81，81+9=90．
故第10行从左边第9个数是90．
故答案为：90．
　
22． 甲、乙两人从同一地点出发，甲每小时走6km，乙每小时走4km，用代数式表示：
（1）反向行走t小时后，两人相距多少千米？
（2）同向行走t小时后，两人相距多少千米？
（3）反向行走，甲比乙早出发m小时，则乙走n小时后，两人相距多少千米？
（4）同向行走，甲比乙晚出发m小时，则乙走n小时后（n＞m），两人相距多少千米？
解：（1）由题意可得：（6+4）t=10t，
答：反向行走t小时后，两人相距10t千米；
（2）由题意可得：（6﹣4）t=2t，
答：同向行走t小时后，两人相距2t千米；
（3）由题意可得：6（m+n ）+4n=6m+10n，
答：乙走n小时后，两人相距（6m+10n）千米；
（4）根据题意可得：|6（n﹣m）﹣4n|=|2n﹣6m|，
答：乙走n小时后（n＞m），两人相距|2n﹣6m|千米．
　
23． 某地电话拨号上网有两种收费方式：A计时制：1.5元/时，B包月制：50元/月，此外每种上网方式都要加收通讯费1元/时．21cnjy.com
（1）某用户某月上网的时间为x小时，请写出两种收费方式下该用户应该支付的费用；
（2）某用户估计一个月上网的时间为30小时，你认为选择哪种方式合算？
解：（1）A种方式的费用=1.5x+x=2.5x，B种方式的费用=50+x；
（2）当x=30时，A种方式的费用=2.5×30=75元；B种方式的费用=50+30=80元．
∵75＜80，
∴选A记时制合算．
　
24． 窗户的形状如图所示（图中长度单位：cm），其上部是半圆形，下部是边长相同的四个小正方形，已知下部小正方形的边长是a cm，计算：21教育名师原创作品
（1）窗户的面积；
（2）窗户的外框的总长．
解：（1）窗户的面积是：
4a2+πa2÷2
=4a2+0.5πa2
=（4+0.5π）a2（cm2）
（2）窗户的外框的总长是：
2a×3+πa
=6a+πa
=（6+π）a（cm）
　
25． 用代数式表示：
①x，y两数的平方差与这两数和的积是　（x﹣y）（x+y）2　；
②x的2倍与x的的和是　x　．
解：①（x2﹣y2）（x+y）=（x﹣y）（x+y）2．
故x，y两数的平方差与这两数和的积是（x﹣y）（x+y）2；
②2x+x=x．
故x的2倍与x的的和是x．
故答案为：（x﹣y）（x+y）2；x．
　
26． 阅读下面材料，完成相应的填空：
（1）双循环与单循环问题：
小田是个足球迷，他发现有的比赛是单循环的，就是每两个球队之间只赛一场；有的比赛是双循环的，每两个球队按主客场要赛两场，同时小田又是个数学迷，他想探究如果有n（n≥2）个球队进行双循环比赛，一共要赛多少场？21*cnjy*com
①小田觉得从特殊情况入手可能会找到灵感，于是他取n=2，要赛2场；n=3，赛6场；n=4，赛12场；那么n=5，要赛　20　场…，由此得出，n（n≥2）个球队进行双循环比赛，一共要赛　n（n﹣1）　场．
②聪明的小田由①中的结论，很快地得出n（n≥2）个球队单循环比赛场数为　　；
（2）知识迁移：①平面内有10个点，且任意3个点不在同一条直线上，经过每两点画一条直线，一共能画　45　条不同的直线．②一个n边形（n≥3）有　　条对角线．
解：（1）①当n=5时，每支球队与另外4支队伍比赛，共有4×5=20场比赛；
n支球队每支球队与其余队伍比赛n﹣1场，共有n（n﹣1）；
②单循环则为；
（2）①当平面上有2个点时，可以画=条直线；
当平面上有3个点时，可以画==3条直线；
…
当平面上有n（n≥2）个点时，可以画条直线；
因此当n=10时，一共可以画（10×9）÷2=45条直线．
②过n边形（n≥3）的一个顶点可以作（n﹣3）条对角线，
这个n边形共有条对角线．
故答案为：20，；45，．
　
27．新学期，两摞规格相同的数学课本整齐的叠放在讲台上，请根据图中所给出的数据信息，解答下列问题：
（1）每本书的高度为　0.5　cm，课桌的高度为　85　cm；
（2）当课本数为x（本）时，请写出同样叠放在桌面上的一摞数学课本高出地面的距离（用含x的代数式表示）；【出处：21教育名师】
（3）桌面上有56本与题（1）中相同的数学课本，整齐叠放成一摞，若从中取走14本，求余下的数学课本高出地面的距离．
解：（1）书的厚度为：（88﹣86.5）÷（6﹣3）=0.5cm；
课桌的高度为：86.5﹣3×0.5=85cm；
故答案为：0.5；85；
（2）∵x本书的高度为0.5x，课桌的高度为85，
∴高出地面的距离为85+0.5x；
（3）当x=56﹣14=42时，85+0.5x=106cm．