浙教版九年级上册第4章相似三角形章末复习课件
文档属性
| 名称 | 浙教版九年级上册第4章相似三角形章末复习课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-26 00:00:00 | ||
图片预览





文档简介
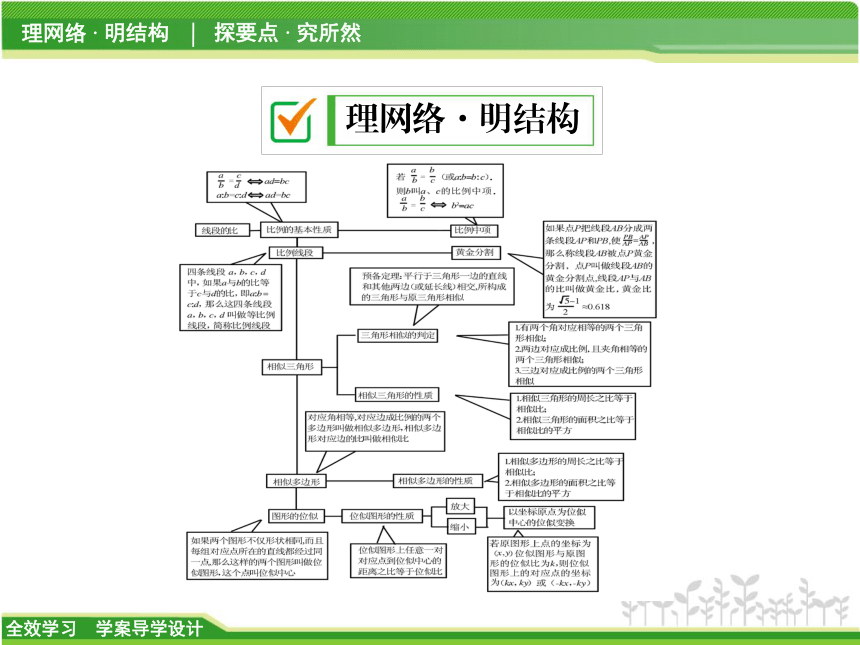
课件20张PPT。第4章 相似三角形章末复习课理网络·明结构探要点·究所然类型之一 平行线分线段成比例定理
在运用平行线分线段成比例定理时要注意弄清三条平行线截两条直线,所得哪条线段与哪条线段是对应线段,同时要根据需要写出正确的比例式.
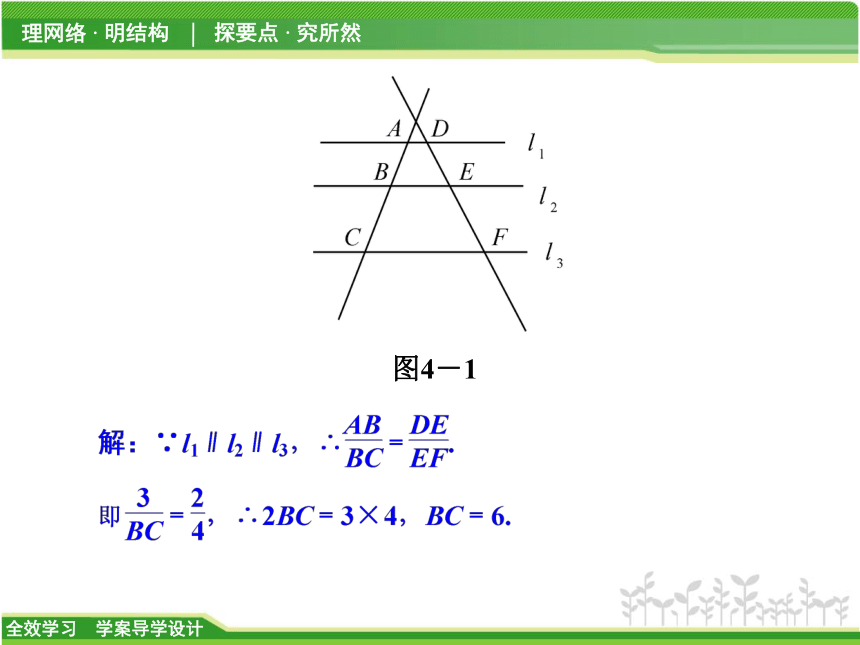
例1 已知:如图4-1,l1∥l2∥l3,AB=3,DE=2,EF=4,求BC.图4-1
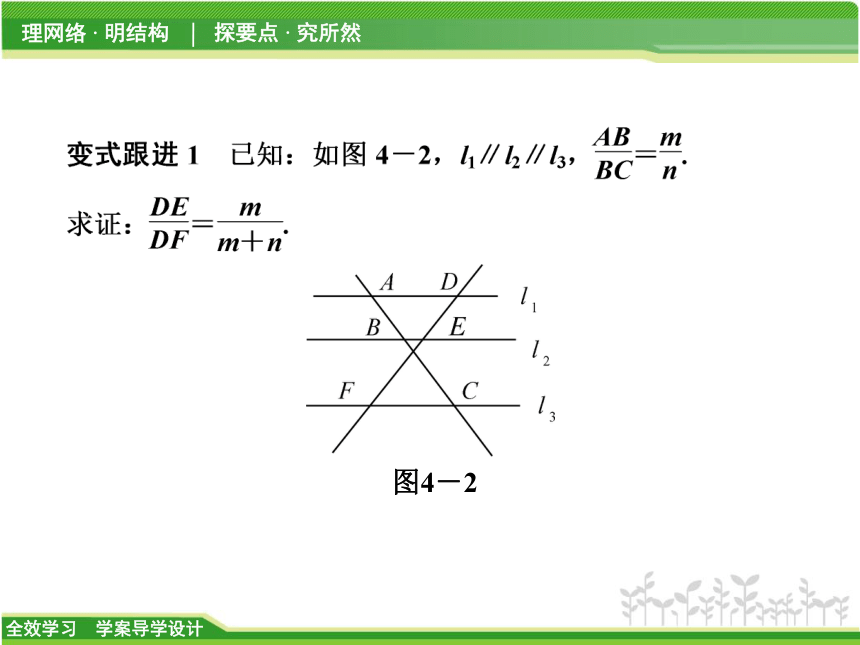
图4-2类型之二 相似三角形的判定
判定两个三角形相似共有四种方法,根据题目的情况灵活选用.选择适当的方法判定两个三角形相似时,要注意找准它们的对应关系.
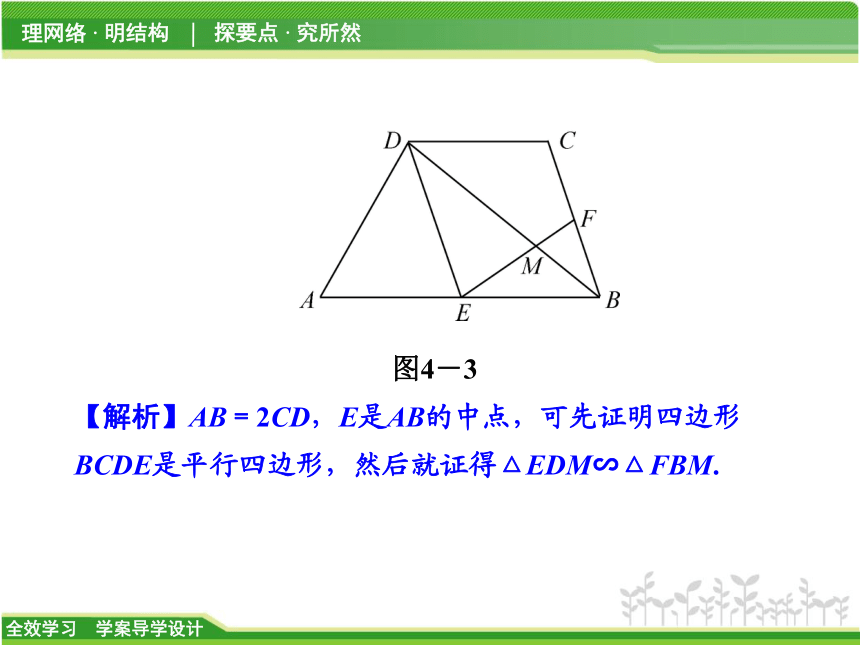
例2 如图4-3所示,四边形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD相交于点M.
(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.图4-3
【解析】AB=2CD,E是AB的中点,可先证明四边形BCDE是平行四边形,然后就证得△EDM∽△FBM.解:(1)证明:∵E是AB的中点,
∴AB=2EB.
∵AB=2CD,∴CD=EB.
又∵AB∥CD,
∴四边形CBED是平行四边形,
∴CB∥DE,
∴∠DEM=∠BFM,∠EDM=∠FBM,
∴△EDM∽△FBM.变式跟进2 如图4-4所示,已知∠1=∠2,若再增加一个条件就能使结论“AB·DE=AD·BC”成立.
(1)写出这个条件(至少写出3个);
(2)对其中的一个予以证明.
图4-4【点悟】 对已知条件和结论先进行正确地分析,然后再
明确需增加条件.类型之三 相似三角形的性质
对应角相等,对应边成比例是相似三角形的基本性质;相似三角形的对应高之比,对应中线之比,对应角平分线之比,周长之比都等于相似比;相似三角形面积之比等于相似比的平方.解题时常需灵活运用这些性质.例3 如图4-5,?ABCD中,E是AB延长线上一点,DE交BC于点F,已知BE∶AB=2∶3,S△BEF=4,求S△CDF.
图4-5变式跟进3 [2014·莱芜]如图4-6,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC,若S△BDE∶S△CDE=1∶4,则S△BDE∶S△ADC为 ( )
A.1∶16 B.1∶18
C.1∶20 D.1∶24图4-6C类型之四 圆中的相似三角形
证明圆中图形的相似问题,常用到垂径定理及其逆定理、圆周角定理及其逆定理进行角度转换.
例4 如图4-7,BD是⊙O的直径,A,C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E.
(1)求证:△ABD∽△AEB;
(2)若AD=1,DE=3,求BD的长.图4-7变式跟进4 如图4-8,△ABC的两个顶点B,C在圆上,顶点A在圆外,AB,AC分别交圆于E,D两点,连结EC,BD.
图4-8(1)求证:△ABD∽△ACE;
(2)若△BEC与△BDC的面积相等,试判定三角形ABC的
形状.
在运用平行线分线段成比例定理时要注意弄清三条平行线截两条直线,所得哪条线段与哪条线段是对应线段,同时要根据需要写出正确的比例式.
例1 已知:如图4-1,l1∥l2∥l3,AB=3,DE=2,EF=4,求BC.图4-1
图4-2类型之二 相似三角形的判定
判定两个三角形相似共有四种方法,根据题目的情况灵活选用.选择适当的方法判定两个三角形相似时,要注意找准它们的对应关系.
例2 如图4-3所示,四边形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD相交于点M.
(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.图4-3
【解析】AB=2CD,E是AB的中点,可先证明四边形BCDE是平行四边形,然后就证得△EDM∽△FBM.解:(1)证明:∵E是AB的中点,
∴AB=2EB.
∵AB=2CD,∴CD=EB.
又∵AB∥CD,
∴四边形CBED是平行四边形,
∴CB∥DE,
∴∠DEM=∠BFM,∠EDM=∠FBM,
∴△EDM∽△FBM.变式跟进2 如图4-4所示,已知∠1=∠2,若再增加一个条件就能使结论“AB·DE=AD·BC”成立.
(1)写出这个条件(至少写出3个);
(2)对其中的一个予以证明.
图4-4【点悟】 对已知条件和结论先进行正确地分析,然后再
明确需增加条件.类型之三 相似三角形的性质
对应角相等,对应边成比例是相似三角形的基本性质;相似三角形的对应高之比,对应中线之比,对应角平分线之比,周长之比都等于相似比;相似三角形面积之比等于相似比的平方.解题时常需灵活运用这些性质.例3 如图4-5,?ABCD中,E是AB延长线上一点,DE交BC于点F,已知BE∶AB=2∶3,S△BEF=4,求S△CDF.
图4-5变式跟进3 [2014·莱芜]如图4-6,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC,若S△BDE∶S△CDE=1∶4,则S△BDE∶S△ADC为 ( )
A.1∶16 B.1∶18
C.1∶20 D.1∶24图4-6C类型之四 圆中的相似三角形
证明圆中图形的相似问题,常用到垂径定理及其逆定理、圆周角定理及其逆定理进行角度转换.
例4 如图4-7,BD是⊙O的直径,A,C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E.
(1)求证:△ABD∽△AEB;
(2)若AD=1,DE=3,求BD的长.图4-7变式跟进4 如图4-8,△ABC的两个顶点B,C在圆上,顶点A在圆外,AB,AC分别交圆于E,D两点,连结EC,BD.
图4-8(1)求证:△ABD∽△ACE;
(2)若△BEC与△BDC的面积相等,试判定三角形ABC的
形状.
同课章节目录
