浙教版九年级下册第二章直线与圆的位置关系章末复习课件
文档属性
| 名称 | 浙教版九年级下册第二章直线与圆的位置关系章末复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-26 19:46:18 | ||
图片预览






文档简介
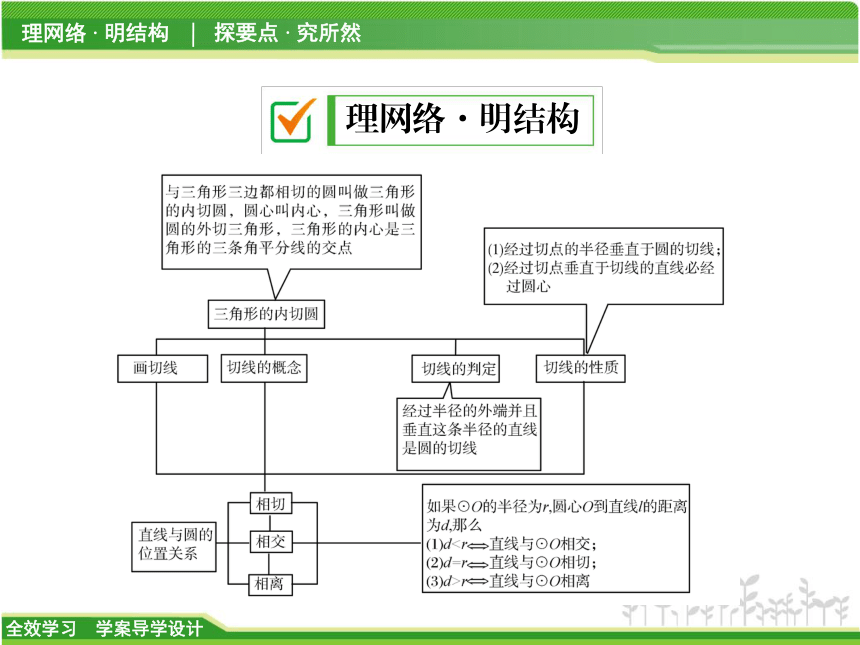
课件20张PPT。第2章 直线与圆的位置关系章末复习课理网络·明结构探要点·究所然类型之一 切线的性质
圆的切线垂直于过切点的半径.如果已知圆的切线,通常作过切点的半径为辅助线,得到直角.
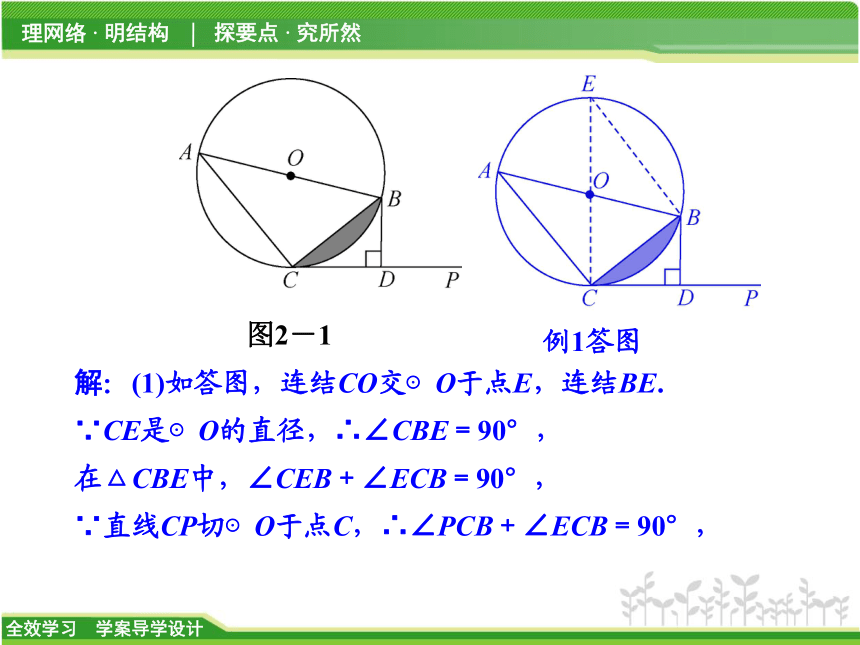
例1 [2014·黔东南]如图2-1,已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于点D.
(1)求证:△ACB∽△CDB.
(2)若⊙O的半径为1,∠BCP=30°,求图中阴影部分的面积. 图2-1
解:(1)如答图,连结CO交⊙O于点E,连结BE.
∵CE是⊙O的直径,∴∠CBE=90°,
在△CBE中,∠CEB+∠ECB=90°,
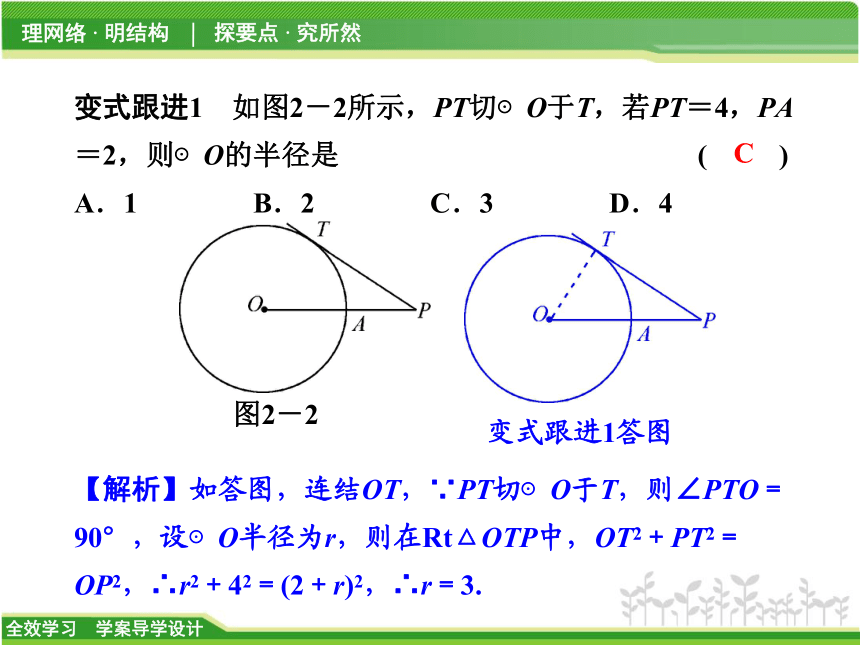
∵直线CP切⊙O于点C,∴∠PCB+∠ECB=90°, 例1答图变式跟进1 如图2-2所示,PT切⊙O于T,若PT=4,PA=2,则⊙O的半径是 ( )
A.1 B.2 C.3 D.4
【解析】如答图,连结OT,∵PT切⊙O于T,则∠PTO=90°,设⊙O半径为r,则在Rt△OTP中,OT2+PT2=OP2,∴r2+42=(2+r)2,∴r=3.
图2-2变式跟进1答图C类型之二 切线的判定
切线的判定方法有:
(1)和圆只有一个公共点的直线是圆的切线;
(2)到圆心的距离等于半径的直线是圆的切线;
(3)经过半径外端且与这条半径垂直的直线是圆的切线.
例2 如图2-3,已知AB是圆O的直径,BC是圆O的弦,弦ED⊥AB于点F,交BC于点G,过点C作圆O的切线与ED的延长线交于点P.
(1)求证:PC=PG;(2)点C在劣弧AD上运动时,其他条件不变,若点G是BC的中点,试探究CG,BF,BO三者之间的数量关系,并写出证明过程;
图2-3
例2答图
解:(1)证明:如答图,连接OC,
∵PC为⊙O的切线,∴OC⊥PC.
∴∠OCG+∠PCG=90°.
∵ED⊥AB,∴∠B+∠BGF=90°.
∵OB=OC,∴∠B=∠OCG,∴∠PCG=∠BGF.又∵∠BGF=∠PGC,∴∠PGC=∠PCG,
∴PC=PG.
(2)CG,BF,BO三者之间的数量关系为CG2=BO·BF.理由如下:
如答图,连接OG,∵点G是BC的中点,
∴OG⊥BC,BG=CG,∴∠OGB=90°.
∵∠OBG=∠GBF,∴Rt△BOG∽Rt△BGF,
∴BG∶BF=BO∶BG.
∴BG2=BO·BF,∴CG2=BO·BF.
【点悟】证明切线,若直线与圆有交点,连结交点与圆心,证明直线与半径垂直,即“有交点,作半径,证垂直”,作过切点的半径也是常用的辅助线.变式跟进2 [2014·临沂] 如图2-4,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连结OE,若BC=4,求△OEC的面积.图2-4变式跟进2答图
解:(1)证明:如答图,连结OD,
∵等腰三角形ABC的底角为30°,
∴∠ABC=∠A=30°,
∵OB=OD,∴∠ABC=∠ODB=30°,∴∠A=∠ODB=30°,∴OD∥AC,
∵DE⊥AC,∴∠ODE=∠DEA=90°,
∴DE是⊙O的切线.
(2)如答图,连结CD,
∵∠B=30°,∴∠COD=60°,
∴△ODC是等边三角形,
∴∠ODC=60°,∴∠CDE=30°,∵BC=4,∴DC=2,
类型之三 切线长定理及三角形的内切圆
解三角形的内切圆的题目时,常连结内心与三角形的顶点或连结经过切点的半径,利用同一个三角形的面积相等求一些线段的长,也是解题中常用的方法.A图2-5例3答图变式跟进3 [2014·日照]如图2-6,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C.
(1)求证:OD∥BE;
(2)如果OD=6 cm,OC=8 cm,求CD的长.图2-6变式跟进3答图
圆的切线垂直于过切点的半径.如果已知圆的切线,通常作过切点的半径为辅助线,得到直角.
例1 [2014·黔东南]如图2-1,已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于点D.
(1)求证:△ACB∽△CDB.
(2)若⊙O的半径为1,∠BCP=30°,求图中阴影部分的面积. 图2-1
解:(1)如答图,连结CO交⊙O于点E,连结BE.
∵CE是⊙O的直径,∴∠CBE=90°,
在△CBE中,∠CEB+∠ECB=90°,
∵直线CP切⊙O于点C,∴∠PCB+∠ECB=90°, 例1答图变式跟进1 如图2-2所示,PT切⊙O于T,若PT=4,PA=2,则⊙O的半径是 ( )
A.1 B.2 C.3 D.4
【解析】如答图,连结OT,∵PT切⊙O于T,则∠PTO=90°,设⊙O半径为r,则在Rt△OTP中,OT2+PT2=OP2,∴r2+42=(2+r)2,∴r=3.
图2-2变式跟进1答图C类型之二 切线的判定
切线的判定方法有:
(1)和圆只有一个公共点的直线是圆的切线;
(2)到圆心的距离等于半径的直线是圆的切线;
(3)经过半径外端且与这条半径垂直的直线是圆的切线.
例2 如图2-3,已知AB是圆O的直径,BC是圆O的弦,弦ED⊥AB于点F,交BC于点G,过点C作圆O的切线与ED的延长线交于点P.
(1)求证:PC=PG;(2)点C在劣弧AD上运动时,其他条件不变,若点G是BC的中点,试探究CG,BF,BO三者之间的数量关系,并写出证明过程;
图2-3
例2答图
解:(1)证明:如答图,连接OC,
∵PC为⊙O的切线,∴OC⊥PC.
∴∠OCG+∠PCG=90°.
∵ED⊥AB,∴∠B+∠BGF=90°.
∵OB=OC,∴∠B=∠OCG,∴∠PCG=∠BGF.又∵∠BGF=∠PGC,∴∠PGC=∠PCG,
∴PC=PG.
(2)CG,BF,BO三者之间的数量关系为CG2=BO·BF.理由如下:
如答图,连接OG,∵点G是BC的中点,
∴OG⊥BC,BG=CG,∴∠OGB=90°.
∵∠OBG=∠GBF,∴Rt△BOG∽Rt△BGF,
∴BG∶BF=BO∶BG.
∴BG2=BO·BF,∴CG2=BO·BF.
【点悟】证明切线,若直线与圆有交点,连结交点与圆心,证明直线与半径垂直,即“有交点,作半径,证垂直”,作过切点的半径也是常用的辅助线.变式跟进2 [2014·临沂] 如图2-4,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连结OE,若BC=4,求△OEC的面积.图2-4变式跟进2答图
解:(1)证明:如答图,连结OD,
∵等腰三角形ABC的底角为30°,
∴∠ABC=∠A=30°,
∵OB=OD,∴∠ABC=∠ODB=30°,∴∠A=∠ODB=30°,∴OD∥AC,
∵DE⊥AC,∴∠ODE=∠DEA=90°,
∴DE是⊙O的切线.
(2)如答图,连结CD,
∵∠B=30°,∴∠COD=60°,
∴△ODC是等边三角形,
∴∠ODC=60°,∴∠CDE=30°,∵BC=4,∴DC=2,
类型之三 切线长定理及三角形的内切圆
解三角形的内切圆的题目时,常连结内心与三角形的顶点或连结经过切点的半径,利用同一个三角形的面积相等求一些线段的长,也是解题中常用的方法.A图2-5例3答图变式跟进3 [2014·日照]如图2-6,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C.
(1)求证:OD∥BE;
(2)如果OD=6 cm,OC=8 cm,求CD的长.图2-6变式跟进3答图
