浙教版九年级下册第三章投影与三视图章末复习课件
文档属性
| 名称 | 浙教版九年级下册第三章投影与三视图章末复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-26 19:52:02 | ||
图片预览





文档简介
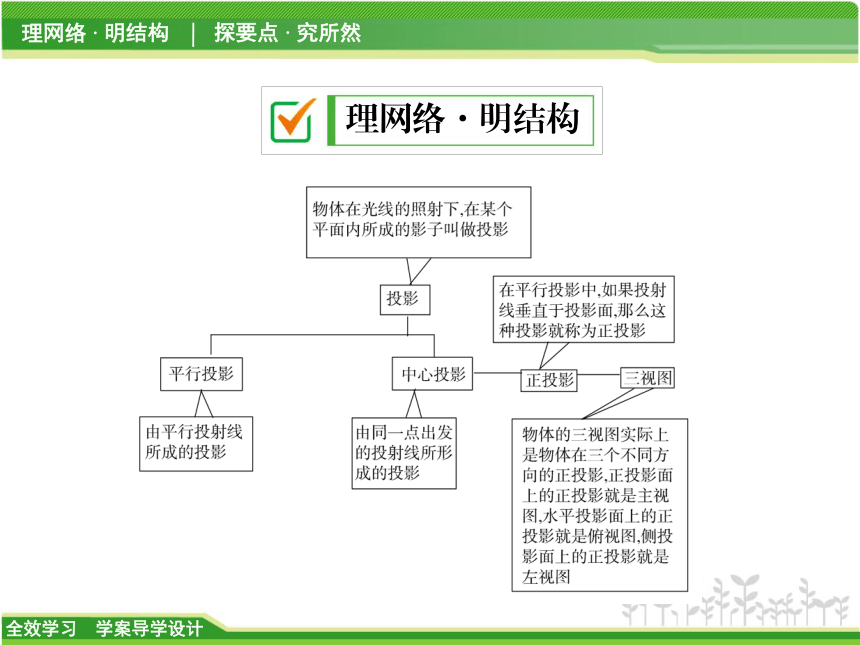
课件21张PPT。第3章 三视图与表面展开图章末复习课理网络·明结构探要点·究所然类型之一 投影
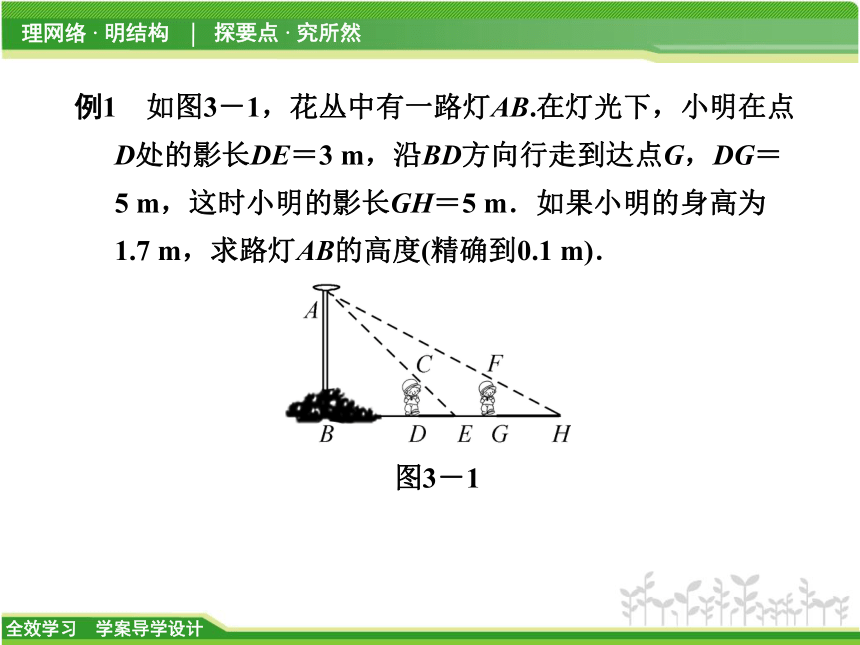
投影分为平行投影与中心投影.平行投影中,同一时刻同一地点,物高与物体在地平线上的影长成正比(相似三角形对应边成比例);在中心投影中,所得投影与物体的平面形状相似.例1 如图3-1,花丛中有一路灯AB.在灯光下,小明在点D处的影长DE=3 m,沿BD方向行走到达点G,DG=5 m,这时小明的影长GH=5 m.如果小明的身高为1.7 m,求路灯AB的高度(精确到0.1 m).
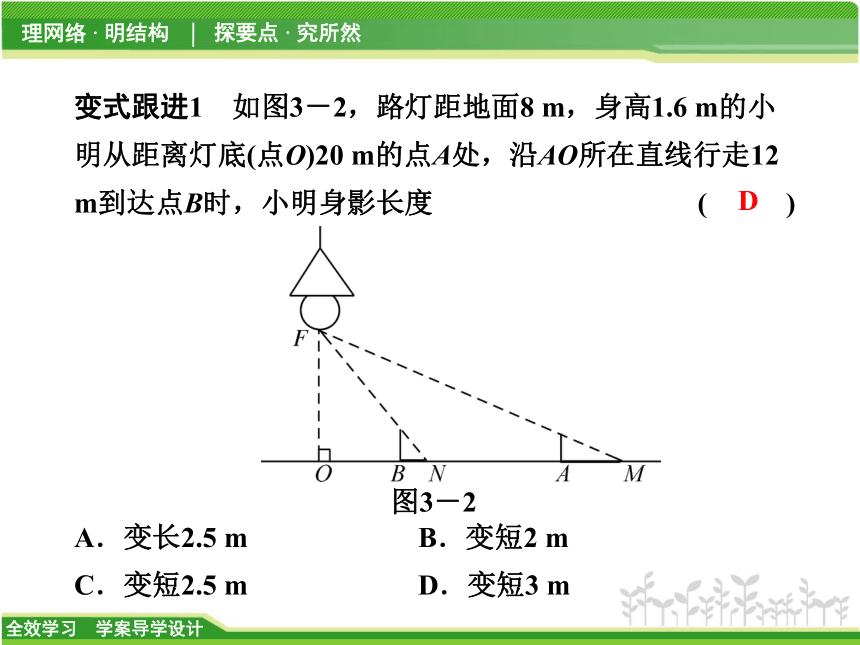
图3-1变式跟进1 如图3-2,路灯距地面8 m,身高1.6 m的小明从距离灯底(点O)20 m的点A处,沿AO所在直线行走12 m到达点B时,小明身影长度 ( )
A.变长2.5 m B.变短2 m
C.变短2.5 m D.变短3 m图3-2D类型之二 物体的三视图
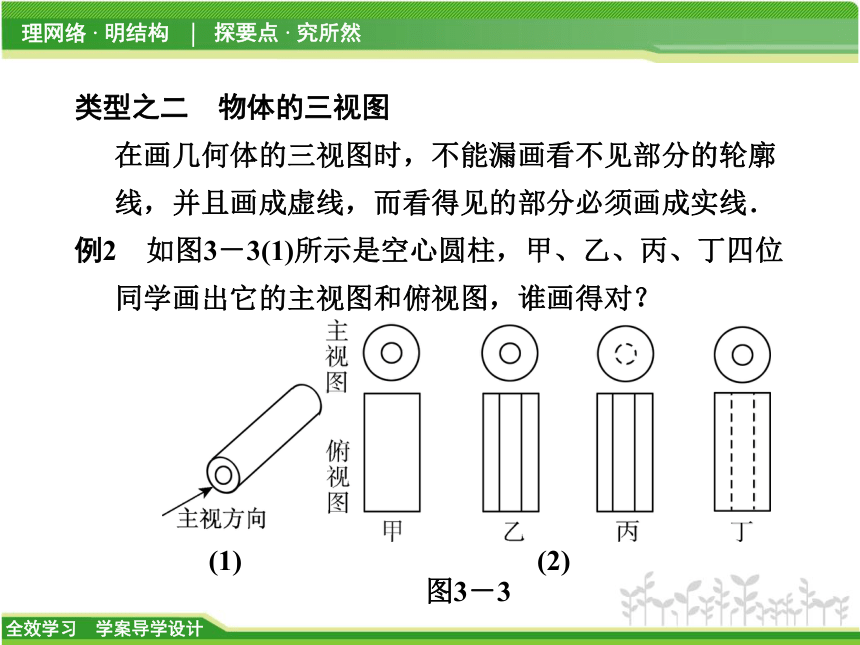
在画几何体的三视图时,不能漏画看不见部分的轮廓线,并且画成虚线,而看得见的部分必须画成实线.
例2 如图3-3(1)所示是空心圆柱,甲、乙、丙、丁四位同学画出它的主视图和俯视图,谁画得对?
图3-3(1) (2)【解析】 画三视图时,看得见的轮廓线画成实线,看不见的轮廓线画成虚线,实线与虚线重叠部分画成实线.
解: 甲同学主视图画对了,但俯视图漏画了内部看不见的轮廓线;乙同学把俯视图中看不见的轮廓线画成实线了;丙同学与乙同学犯了同样的错误,另外丙同学的主视图也画错了,内部的小圆圈属于看得见的轮廓线,应画实线,只有丁同学画对了.变式跟进2 下列几何体中,主视图是圆形的是 ( )
A B C D
A类型之三 物体的侧面积与全面积
根据三视图画出实物图,并会拆分实物图.
例3 如图3-4,将一张正方形纸片的4个角剪去4个大小一样的小正方形,然后折起来就可以制成一个无盖的长方体纸盒,设这个正方形纸片的边长为a,这个无盖的长方体盒子高为h.图3-4(1)若a=18 cm,h=4 cm,则这个无盖长方体盒子的底面面积为____________;
(2)用含a和h的代数式表示这个无盖长方体盒子的容积V=_____________;
(3)若a=18 cm,试探究:当h越大,无盖长方体盒子的容积V就越大吗?请举例说明;这个无盖长方体盒子的最大容积是__________.
【解析】(1)根据已知得出长方体底面的边长进而求出即可;
(2)利用底面积乘高得出无盖长方体盒子的容积即可;
(3)根据材料一定长方体中体积最大与底面积和高都有关,进而得出答案.100 cm2h(a-2h)2432 cm3解:(1)∵a=18 cm,h=4 cm,
∴这个无盖长方体盒子的底面面积为:(a-2h)(a-2h)=(18-2×4)×(18-2×4)=100(cm2);
(2)这个无盖长方体盒子的容积V=h(a-2h)(a-2h)=h(a-2h)2;
(3)若a=18 cm,当h越大,无盖长方体盒子的容积V不一定就越大,
∵V=h(18-2h)2,只有h=3时,此时体积最大,
∴这个无盖长方体盒子的最大容积是:3×(18-6)2=432(cm3).变式跟进3 已知某正六棱柱的主视图如图3-5所示.
(1)求该六棱柱的表面积;
(2)求该六棱柱的体积.图3-5【点悟】 由主视图中可得到正六棱柱的底面棱长和高,
故表面积和体积可求.类型之四 探索正方体的个数
先根据主视图和左视图确定出俯视图中每个小正方形相应的位置上的小正方体的个数,再求出组成这个几何体所需小正方体的个数,具体方法如下:
(1)根据主视图,数出从左到右每列中的小正方形的个数,在俯视图从左到右对应的列中每个小正方形内都填入相应的数字;
(2)根据左视图,数出从左到右每列中的小正方形个数,在俯视图从上到下对应的行中每个小正方形内也都填入相应的数字;(3)取俯视图中每个小正方形内填入的一对数中的较小的一个,并把它们相加,所得结果就是组成这个几何体所需小正方体的个数.
例4 在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来.如图3-6所示,则这堆正方体货箱共有 ( )
A.9箱 B.10箱
C.11箱 D.12箱图3-6A【解析】 观察主视图,各个位置的小正方体的个数用①,②,③在俯视图中表示[如答图(1)].
观察左视图,各个位置的小正方体的个数用1,2,3在俯视图中表示[如答图(1)].
(1) (2)
例4答图
取各小方格内最小的数字,即为所求,如答图(2),故选择A.变式跟进4 如图3-7,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,搭成一个长方体,那么最少还需要______个小立方块.图3-726【解析】 由俯视图易得最底层有7个小立方块,第二层有2个小立方块,第三层有1个小立方块,那么该几何体共由7+2+1=10(个)小立块体组成.若搭成一个长方体,最少需4×3×3=36(个)小立方块,所以还需36-10=26(个)小立方块.
投影分为平行投影与中心投影.平行投影中,同一时刻同一地点,物高与物体在地平线上的影长成正比(相似三角形对应边成比例);在中心投影中,所得投影与物体的平面形状相似.例1 如图3-1,花丛中有一路灯AB.在灯光下,小明在点D处的影长DE=3 m,沿BD方向行走到达点G,DG=5 m,这时小明的影长GH=5 m.如果小明的身高为1.7 m,求路灯AB的高度(精确到0.1 m).
图3-1变式跟进1 如图3-2,路灯距地面8 m,身高1.6 m的小明从距离灯底(点O)20 m的点A处,沿AO所在直线行走12 m到达点B时,小明身影长度 ( )
A.变长2.5 m B.变短2 m
C.变短2.5 m D.变短3 m图3-2D类型之二 物体的三视图
在画几何体的三视图时,不能漏画看不见部分的轮廓线,并且画成虚线,而看得见的部分必须画成实线.
例2 如图3-3(1)所示是空心圆柱,甲、乙、丙、丁四位同学画出它的主视图和俯视图,谁画得对?
图3-3(1) (2)【解析】 画三视图时,看得见的轮廓线画成实线,看不见的轮廓线画成虚线,实线与虚线重叠部分画成实线.
解: 甲同学主视图画对了,但俯视图漏画了内部看不见的轮廓线;乙同学把俯视图中看不见的轮廓线画成实线了;丙同学与乙同学犯了同样的错误,另外丙同学的主视图也画错了,内部的小圆圈属于看得见的轮廓线,应画实线,只有丁同学画对了.变式跟进2 下列几何体中,主视图是圆形的是 ( )
A B C D
A类型之三 物体的侧面积与全面积
根据三视图画出实物图,并会拆分实物图.
例3 如图3-4,将一张正方形纸片的4个角剪去4个大小一样的小正方形,然后折起来就可以制成一个无盖的长方体纸盒,设这个正方形纸片的边长为a,这个无盖的长方体盒子高为h.图3-4(1)若a=18 cm,h=4 cm,则这个无盖长方体盒子的底面面积为____________;
(2)用含a和h的代数式表示这个无盖长方体盒子的容积V=_____________;
(3)若a=18 cm,试探究:当h越大,无盖长方体盒子的容积V就越大吗?请举例说明;这个无盖长方体盒子的最大容积是__________.
【解析】(1)根据已知得出长方体底面的边长进而求出即可;
(2)利用底面积乘高得出无盖长方体盒子的容积即可;
(3)根据材料一定长方体中体积最大与底面积和高都有关,进而得出答案.100 cm2h(a-2h)2432 cm3解:(1)∵a=18 cm,h=4 cm,
∴这个无盖长方体盒子的底面面积为:(a-2h)(a-2h)=(18-2×4)×(18-2×4)=100(cm2);
(2)这个无盖长方体盒子的容积V=h(a-2h)(a-2h)=h(a-2h)2;
(3)若a=18 cm,当h越大,无盖长方体盒子的容积V不一定就越大,
∵V=h(18-2h)2,只有h=3时,此时体积最大,
∴这个无盖长方体盒子的最大容积是:3×(18-6)2=432(cm3).变式跟进3 已知某正六棱柱的主视图如图3-5所示.
(1)求该六棱柱的表面积;
(2)求该六棱柱的体积.图3-5【点悟】 由主视图中可得到正六棱柱的底面棱长和高,
故表面积和体积可求.类型之四 探索正方体的个数
先根据主视图和左视图确定出俯视图中每个小正方形相应的位置上的小正方体的个数,再求出组成这个几何体所需小正方体的个数,具体方法如下:
(1)根据主视图,数出从左到右每列中的小正方形的个数,在俯视图从左到右对应的列中每个小正方形内都填入相应的数字;
(2)根据左视图,数出从左到右每列中的小正方形个数,在俯视图从上到下对应的行中每个小正方形内也都填入相应的数字;(3)取俯视图中每个小正方形内填入的一对数中的较小的一个,并把它们相加,所得结果就是组成这个几何体所需小正方体的个数.
例4 在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来.如图3-6所示,则这堆正方体货箱共有 ( )
A.9箱 B.10箱
C.11箱 D.12箱图3-6A【解析】 观察主视图,各个位置的小正方体的个数用①,②,③在俯视图中表示[如答图(1)].
观察左视图,各个位置的小正方体的个数用1,2,3在俯视图中表示[如答图(1)].
(1) (2)
例4答图
取各小方格内最小的数字,即为所求,如答图(2),故选择A.变式跟进4 如图3-7,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,搭成一个长方体,那么最少还需要______个小立方块.图3-726【解析】 由俯视图易得最底层有7个小立方块,第二层有2个小立方块,第三层有1个小立方块,那么该几何体共由7+2+1=10(个)小立块体组成.若搭成一个长方体,最少需4×3×3=36(个)小立方块,所以还需36-10=26(个)小立方块.
