七年级数学上册4.6整式的加减(1)课件
文档属性
| 名称 | 七年级数学上册4.6整式的加减(1)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 718.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-27 11:44:50 | ||
图片预览





文档简介
课件13张PPT。4.6 整式的加减 (1) 如图,用火柴棍拼成一排正方形图形,如果图形
中含有1、2、3或4个正方形,分别需要多少根火柴棍?
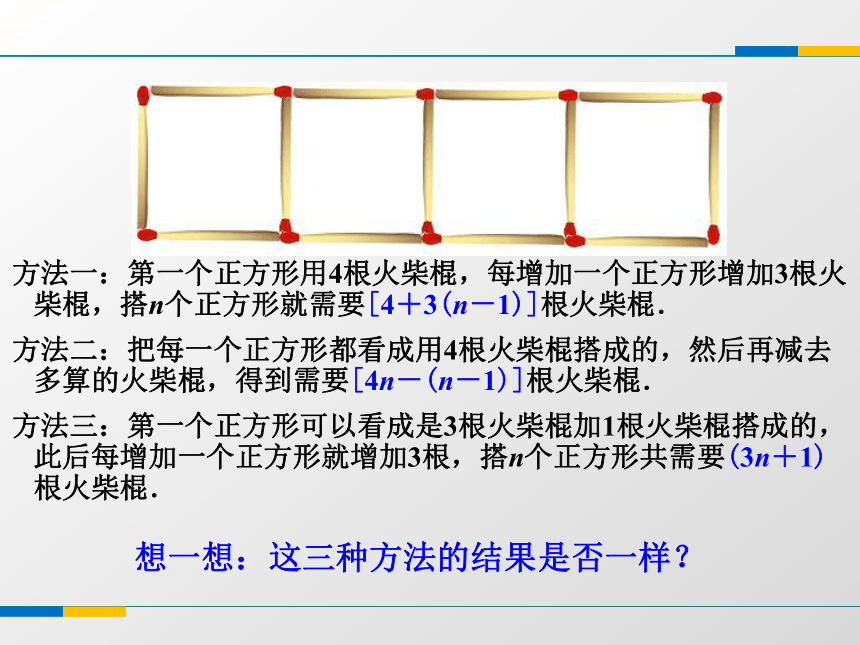
如果图形中含有n个正方形,需要多少根火柴棍?探究新知方法一:第一个正方形用4根火柴棍,每增加一个正方形增加3根火柴棍,搭n个正方形就需要[4+3(n-1)]根火柴棍.
方法二:把每一个正方形都看成用4根火柴棍搭成的,然后再减去多算的火柴棍,得到需要[4n-(n-1)]根火柴棍.
方法三:第一个正方形可以看成是3根火柴棍加1根火柴棍搭成的,此后每增加一个正方形就增加3根,搭n个正方形共需要(3n+1)根火柴棍.想一想:这三种方法的结果是否一样?我们看以下两个简单问题:
(1)4+(3-1)
(2)4-(3-1)解(1)4+(3-1) (1)4+ (3-1)
=4 + 2 =4+3-1
=6 =6类比探究解(2)4-(3-1) (2)4-(3-1)
=4-2 =4-3+1
=2 =2我们看以下两个简单问题:
(1)4+(3-1)
(2)4-(3-1)4+3(n-1)应如何计算?
4n-(n-1)应如何计算?解:
4+3(n-1)
=4+3n-3
=3n+1 4n-(n-1)
=4n-n+1
=3n+1方法一:第一个正方形用4根火柴棍,每增加一个正方形增加3根火柴棍,搭n个正方形就需要[4+3(n-1)]根火柴棍.
方法二:把每一个正方形都看成用4根火柴棍搭成的,然后再减去多算的火柴棍,得到需要[4n-(n-1)]根火柴棍.
方法三:第一个正方形可以看成是3根火柴棍加1根火柴棍搭成的,此后每增加一个正方形就增加3根,搭n个正方形共需要(3n+1)根火柴棍. 所以以上三种方法的结果是一样的,搭n个正方形共需要(3n+1)根火柴棍.探究归纳去括号法则: 括号前是“+”号,把括号和它前面的“+”号
去掉,括号里各项都不变号; 括号前是“-”号,把括号和它前面的“-”号
去掉,括号里各项都改变符号.例1、将下列各式去括号:
(1)+(2a-3b) (2)-( ) (3)-3 ( ) 解:(1)2a-3b(2)(3)例题探究例2、化简并求值:那么当a=-2,b=3时,原式= ab = -6课堂练习解:1、化简下列各式:
(1)8a+2b+(5a-b);
(2)(5a-3b)-3( ).(1)原式=8a+2b+5a-b
= 13a+b (2)原式=5a-3b-3(a2-3b)
=5a-3b-3a2+6b
=-3a2+ 5a +3b2、两船从同一港口同时出发反向而行,甲船顺水,
乙船逆水,两船在静水中的速度都是50 km/h,
水流速度是a km/h.
(1)2 h后两船相距多远?
(2)2 h后甲船比乙船多航行多少km?解:(1) 2(50+a)+2(50-a)
=100+2a+100-2a
=200(km)
(2) 2(50+a)-2(50-a)
=100+2a-100+2a
=4a(km)1. 数学思想方法——类比
2. 去括号法则:
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
3. 注意:去括号规律要准确理解,去括号应考虑括号内的每一项的符号,做到要变都变;要不变都不变;另外,括号内原来有几项,去掉括号后仍有几项. 课堂小结
中含有1、2、3或4个正方形,分别需要多少根火柴棍?
如果图形中含有n个正方形,需要多少根火柴棍?探究新知方法一:第一个正方形用4根火柴棍,每增加一个正方形增加3根火柴棍,搭n个正方形就需要[4+3(n-1)]根火柴棍.
方法二:把每一个正方形都看成用4根火柴棍搭成的,然后再减去多算的火柴棍,得到需要[4n-(n-1)]根火柴棍.
方法三:第一个正方形可以看成是3根火柴棍加1根火柴棍搭成的,此后每增加一个正方形就增加3根,搭n个正方形共需要(3n+1)根火柴棍.想一想:这三种方法的结果是否一样?我们看以下两个简单问题:
(1)4+(3-1)
(2)4-(3-1)解(1)4+(3-1) (1)4+ (3-1)
=4 + 2 =4+3-1
=6 =6类比探究解(2)4-(3-1) (2)4-(3-1)
=4-2 =4-3+1
=2 =2我们看以下两个简单问题:
(1)4+(3-1)
(2)4-(3-1)4+3(n-1)应如何计算?
4n-(n-1)应如何计算?解:
4+3(n-1)
=4+3n-3
=3n+1 4n-(n-1)
=4n-n+1
=3n+1方法一:第一个正方形用4根火柴棍,每增加一个正方形增加3根火柴棍,搭n个正方形就需要[4+3(n-1)]根火柴棍.
方法二:把每一个正方形都看成用4根火柴棍搭成的,然后再减去多算的火柴棍,得到需要[4n-(n-1)]根火柴棍.
方法三:第一个正方形可以看成是3根火柴棍加1根火柴棍搭成的,此后每增加一个正方形就增加3根,搭n个正方形共需要(3n+1)根火柴棍. 所以以上三种方法的结果是一样的,搭n个正方形共需要(3n+1)根火柴棍.探究归纳去括号法则: 括号前是“+”号,把括号和它前面的“+”号
去掉,括号里各项都不变号; 括号前是“-”号,把括号和它前面的“-”号
去掉,括号里各项都改变符号.例1、将下列各式去括号:
(1)+(2a-3b) (2)-( ) (3)-3 ( ) 解:(1)2a-3b(2)(3)例题探究例2、化简并求值:那么当a=-2,b=3时,原式= ab = -6课堂练习解:1、化简下列各式:
(1)8a+2b+(5a-b);
(2)(5a-3b)-3( ).(1)原式=8a+2b+5a-b
= 13a+b (2)原式=5a-3b-3(a2-3b)
=5a-3b-3a2+6b
=-3a2+ 5a +3b2、两船从同一港口同时出发反向而行,甲船顺水,
乙船逆水,两船在静水中的速度都是50 km/h,
水流速度是a km/h.
(1)2 h后两船相距多远?
(2)2 h后甲船比乙船多航行多少km?解:(1) 2(50+a)+2(50-a)
=100+2a+100-2a
=200(km)
(2) 2(50+a)-2(50-a)
=100+2a-100+2a
=4a(km)1. 数学思想方法——类比
2. 去括号法则:
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
3. 注意:去括号规律要准确理解,去括号应考虑括号内的每一项的符号,做到要变都变;要不变都不变;另外,括号内原来有几项,去掉括号后仍有几项. 课堂小结
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
