1.1认识三角形(第2课时)课件

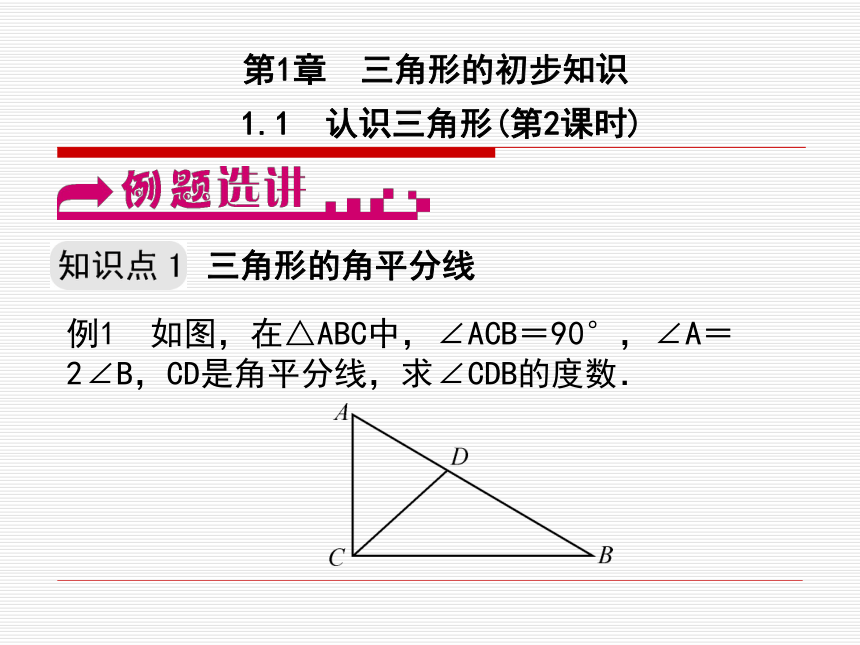
课件16张PPT。第1章　三角形的初步知识1.1　认识三角形(第2课时)三角形的角平分线例1　如图，在△ABC中，∠ACB＝90°，∠A＝2∠B，CD是角平分线，求∠CDB的度数．分析：先由∠ACB＝90°，∠A＝2∠B以及三角形内角和的性质求出∠A、∠B的度数，再根据CD是角平分线可以求出∠DCB的度数，最后再利用内角和为180°即可求出∠CDB.
解：∵∠A＋∠B＋∠ACB＝180°，且∠ACB＝90°∴∠A＋∠B＝90°
∵∠A＝2∠B　
∴∠B＝30°
∵CD是角平分线
∴∠DCB＝45°
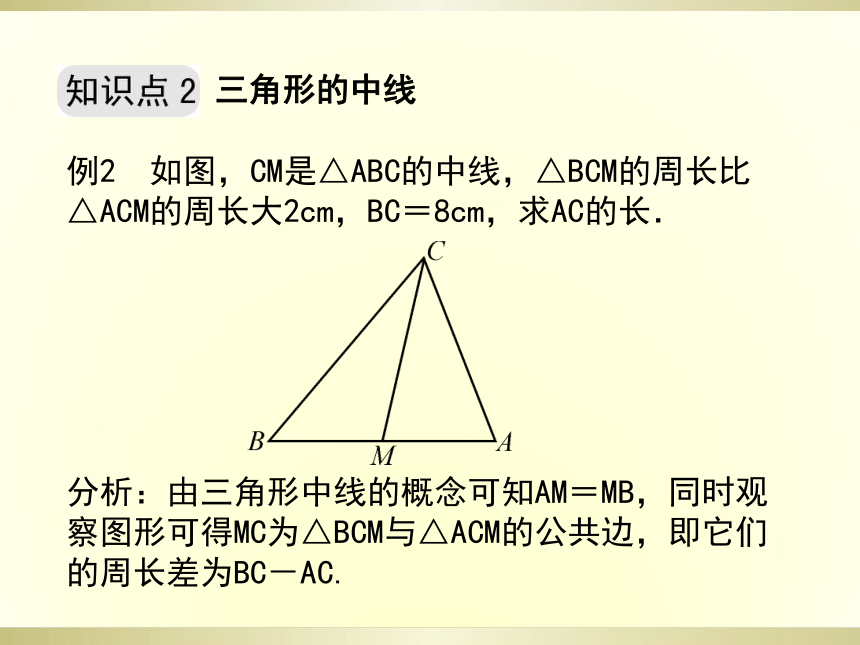
∴∠CDB＝180°－∠DCB－∠B＝180°－45°－30°＝105°注意点：在求解此类问题时，往往会同时运用“角平分线的性质”以及“三角形的内角和为180°”这两个结论．三角形的中线例2　如图，CM是△ABC的中线，△BCM的周长比△ACM的周长大2cm，BC＝8cm，求AC的长．
分析：由三角形中线的概念可知AM＝MB，同时观察图形可得MC为△BCM与△ACM的公共边，即它们的周长差为BC－AC.解：∵△BCM的周长比△ACM的周长大2cm
∴BC＋CM＋BM－(AC＋CM＋AM)＝2cm
又∵CM是△ABC的中线，
∴AM＝MB
∴BC－AC＝2cm　
又∵BC＝8cm　
∴AC＝6cm.
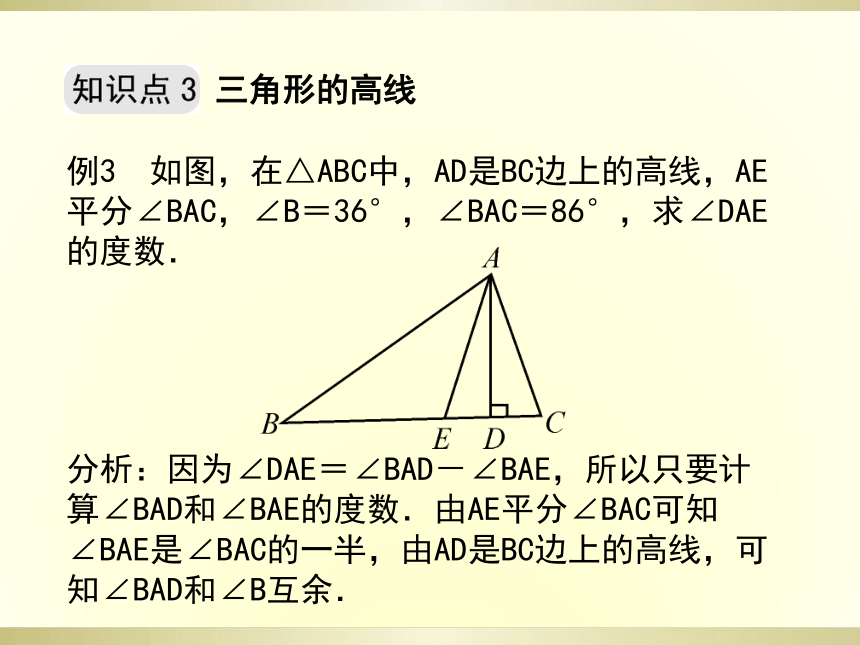
注意点：解题时要利用三角形中线的性质，有时如果没有图形的话要注意可能有两种情况．三角形的高线例3　如图，在△ABC中，AD是BC边上的高线，AE平分∠BAC，∠B＝36°，∠BAC＝86°，求∠DAE的度数．
分析：因为∠DAE＝∠BAD－∠BAE，所以只要计算∠BAD和∠BAE的度数．由AE平分∠BAC可知∠BAE是∠BAC的一半，由AD是BC边上的高线，可知∠BAD和∠B互余．解：∵AE平分∠BAC，∠BAC＝86°，
∴∠BAE＝ ∠BAC＝43°
∵AD是BC边上的高线　 ∴∠ADB＝90°
∴∠BAD＝90°－∠B＝90°－36°＝54°
∴∠DAE＝∠BAD－∠BAE＝54°－43°＝11°
注意点：高线、角平分线结合的问题要注意综合利用它们的性质求解，还应注意三角形内角和180°的合理使用．
三角形的中线的应用例4　如图，在△ABC中，若点D，E，F分别为BC，AD，CE的中点，且S△ABC＝4cm2，则△BEF的面积等于(　　)
A．2cm2
B．1cm2
C. cm2
D. cm2分析：本题从表面上看无法求解，但我们可以根据“三角形的中线把三角形分为面积相等的两部分”这一特征求解．因为D是边BC的中点，
所以S△ABD＝S△ACD＝ S△ABC＝ ×4＝2(cm2)．因
为E是AD边的中点，所以S△BDE＝ S△ABD＝1(cm2)，
S△CDE＝ S△ACD＝1(cm2)，所以S△BEC＝S△BDE＋
S△CDE＝2(cm2)．又因为F是CE的中点，所以S△BEF
＝ S△BEC＝1(cm2)，故选B.
解：B
注意点：同底(或等底)且同高(或等高)的两个三角形面积相等是一条非常有用的结论，同学们应该掌握并运用．三角形的高线的应用例5　如图，在△ABC中，若CE⊥AB，AD⊥BC，且AB＝3，BC＝6.则CE与AD有怎样的数量关系？分析：由△ABC的面积
又因为AB，BC已知，所以可求出CE与AD之间的数量关系．
解：根据△ABC的面积
得3CE＝6AD，即CE＝2AD.
注意点：有高线时，用面积相等来列式．
例1　如图，已知△ABC，用量角器和刻度尺画出AC边上的中线，∠C的角平分线．
错答：如图，BD就是所作的中线，CE就是所作的角平分线．
正答：如图，BD就是所作的中线，CE就是所作的角平分线．
错因：没有正确地理解三角形的角平分线定义，忽略了这些线都是线段，而求作的线都要画成实线．错答图正答图例2　如图，在△ABC中，AB＝20cm，BD⊥AB，BD＝16cm，CE⊥AB，BE＝14cm，CE＝26cm，求△ABC的面积．
错答：∵AB＝20cm，BD＝16cm，BD⊥AB
∴S△ABC＝
正答：∵CE＝26cm，CE是△ABC中AB边上的高线
∴S△ABC＝
错因：对三角形的高线概念理解错误，找错了三角形的高线．