1.3证明(第2课时)课件

课件17张PPT。第1章　三角形的初步知识1.3　证明(第2课时)三角形的内角和定理证明例1　课本中给出了三角形内角和定理的一种证明方法，你还有其他的证明方法吗？
已知：如图，∠A、∠B、∠C
是△ABC的三个内角．
求证：∠A＋∠B＋∠C＝180°
分析：受课本证明的启发，我们不妨把三角形的三个内角转化到任意一点为顶点的一个平角上即可解决问题，也可以尝试将三角形的三个内角转化为两个(或四个)角的和等于180°的方法证明．
解：(方法一)如图1，延长BC到点E，过点C作CF∥AB，则∠A＝∠ACF，∠B＝∠FCE.∴∠A＋∠B＋∠C＝∠ACF＋∠FCE＋∠ACB＝180°.(方法二)如图2，在BC边上任取一点D，过点D作DE∥AB交AC于点E，DF∥AC交AB于点F.
∵DE∥AB　∴∠1＝∠B，∠2＝∠4.
∵DF∥AC　∴∠3＝∠C，∠A＝∠4　 ∴∠2＝∠A
又∵∠2＋∠3＋∠1＝180°　∴∠A＋∠B＋∠C＝180°.
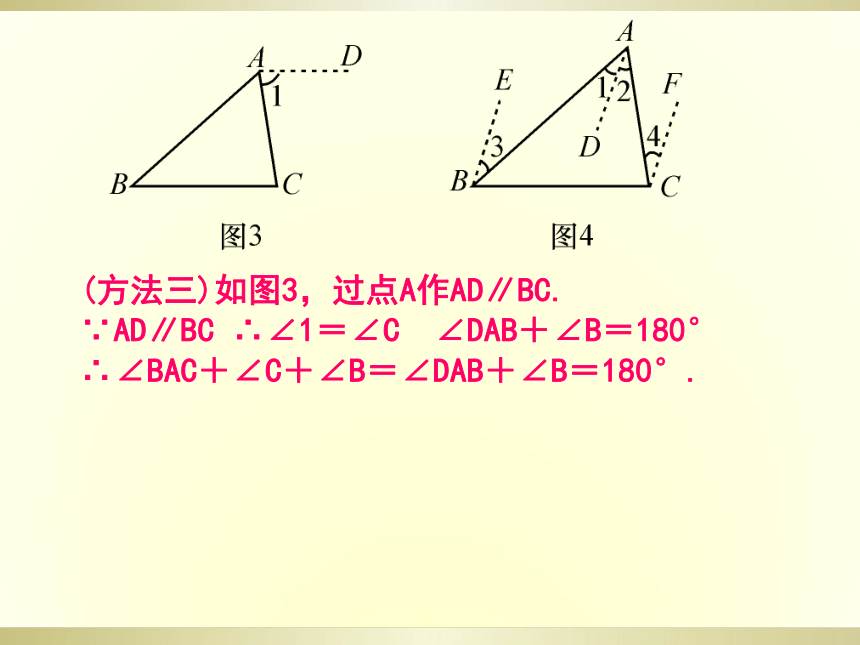
(方法三)如图3，过点A作AD∥BC.
∵AD∥BC ∴∠1＝∠C　∠DAB＋∠B＝180°
∴∠BAC＋∠C＋∠B＝∠DAB＋∠B＝180°.
(方法四)如图4，过点A任作一条射线AD，再作BE∥AD，CF∥AD.∵BE∥AD∥CF　
∴∠1＝∠3，∠2＝∠4，∠EBC＋∠BCF＝180°
∴∠BAC＋∠ABC＋∠ACB＝∠EBC＋∠BCF＝180°.
注意点：对于同一个题目，往往有多种证明方法，可以从一种方法中得出基本思路，运用发散思维，探索多种途径，从而得到多种方法．三角形的外角及外角的性质例2　如图所示，D是△ABC的边BC上一点，∠B＝∠BAD，∠ADC＝80°，∠BAC＝70°
(1)求∠B的度数；
(2)求∠C的度数．
分析：利用三角形外角的性质可求出∠B的度数，再利用三角形内角和求出∠C的度数．解：(1)∵∠ADC是△ABD的外角　
∴∠ADC＝∠B＋∠BAD＝80°
又∵∠B＝∠BAD　
∴∠B＝80°× ＝40°.
(2)∵∠B＋∠BAC＋∠C＝180°　∴∠C＝180°－∠B－∠BAC＝180°－40°－70°＝70°.
注意点：本题也可以根据三角形外角性质得∠ADB＝∠C＋∠CAD，且可得∠CAD＝30°，∠ADB＝100°，所以∠C＝∠ADB－∠CAD＝100°－30°＝70°.变式：如图所示，点D为△ABC内一点，∠ABD＝20°，∠ACD＝25°，∠A＝35°，求∠BDC的度数．
解：延长BD交AC于点E.
∵∠BDC是△CDE的外角，
∴∠BDC＝∠DEC＋∠ACD
又∵∠DEC是△AEB的外角，
∴∠DEC＝∠A＋∠ABD
∴∠BDC＝∠A＋∠ABD＋∠ACD＝35°＋20°＋25°＝80°
证明几何命题的步骤例3　证明命题“一个角的两边分别平行于另一个角的两边，且方向相同，则这两个角相等”是真命题．
分析：根据平行得同位角相等，再利用第三个角的桥梁作用，即可证明两个角相等．
已知：如图，AB∥A′B′，
BC∥B′C′.求证：∠B＝∠B′.证明：∵AB∥A′B′　　
∴∠B′＝∠α
∵BC∥B′C′　　
∴∠B＝∠α　
∴∠B＝∠B′
注意点：证明几何命题要注意步骤的完整，要先画图，后写已知求证，然后才是证明过程．并且证明过程中的每一步推理都要有依据．
利用证明解决实际问题例4 一个零件的形状如图，按规定∠BAC应为90°，∠B，∠C应分别为31°和26°，工人师傅在检测时测得∠BDC＝152°，请判断这个零件是否符合规定，为什么？
分析：方法一：如图1，连结AD并延长到点E，把∠CDB分割成两个角∠CDE，∠BDE，则这两个角分别是△ACD，△ABD的外角，然后进行计算检验．方法二：如图2，延长CD交AB于点F，则∠BFD是△ACF的外角，∠CDB是△BDF的外角，利用三角形的一个外角等于与它不相邻的两个内角的和来解决．
解：方法一：该零件不符合规定．理由：连结AD并延长到点E，如图1
∵∠CDE＝∠C＋∠CAD，∠BDE＝∠B＋∠BAD，
∴∠CDE＋∠BDE＝∠B＋∠C＋∠CAD＋∠BAD，
即∠CDB＝∠B＋∠C＋∠BAC.
又∵152°≠31°＋26°＋90°，
∴该零件不符合规定．
方法二：该零件不符合规定．
理由：如图2，延长CD交AB于点F.
∵∠BFD＝∠A＋∠C，∠CDB＝∠BFD＋∠B，
∴∠CDB＝∠A＋∠B＋∠C.
又∵152°≠31°＋26°＋90°，
∴这个零件不符合规定．
注意点：为了证明的需要，经常在原图形的基础上适当添加辅助线，这种辅助线往往能起到联系未知与已知的“桥梁”作用．例　如图，在△ABC中，∠1是它的一个外角，E为边AC上一点，延长BC到点D，连结DE，求证：∠1＞∠D.
错答：如图，∠1是钝角，∠D是锐角，所以∠1＞∠D
正答：∵∠1是△ABC的一个外角　
∴∠1＞∠ACB
∵∠ACB是△CDE的一个外角
∴∠ACB＞∠D
∴∠1＞∠D
错因：忽略了证明过程中推理的依据，说明角度的大小关系要通过定理推理得到，不能直接从图形中得出一些结论．