2.2　等腰三角形课件

课件6张PPT。第2章　特殊三角形2.2　等腰三角形等腰三角形及其相关概念例1　已知等腰三角形的两边长分别为2和7，则它的周长是(　　)
　　　　　　　　　　　　
A．9 B．11
C．16 D．11或16分析：根据等腰三角形概念可得第三边为2或7，再根据三角形三边关系判断三边为2，7，7，得周长为16.
解：C
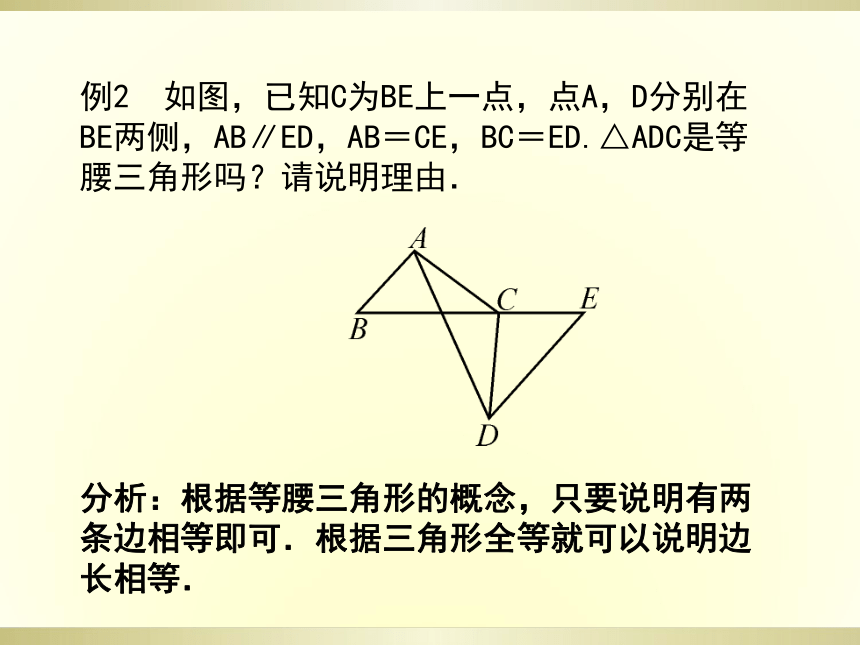
注意点：已知等腰三角形的两边长，求它的周长有两种情况，即已知两边长分别为腰长和底边长时得出的周长有两种情况，但要注意根据三角形三边关系判断是否能组成三角形．例2　如图，已知C为BE上一点，点A，D分别在BE两侧，AB∥ED，AB＝CE，BC＝ED.△ADC是等腰三角形吗？请说明理由．
分析：根据等腰三角形的概念，只要说明有两条边相等即可．根据三角形全等就可以说明边长相等．解：∵AB∥ED　
∴∠B＝∠E　在△ABC和△CED中
∴△ABC≌△CED(SAS)　
∴AC＝CD　
∴△ADC是等腰三角形
注意点：通过三角形全等证明线段相等是判定等腰三角形的一种常见方法．
等边三角形例3　如果一个等边三角形的一边长为6cm，那么这个等边三角形的周长是______．
分析：由题意得等边三角形的周长为6×3＝18cm.
解：18cm
注意点：由等边三角形的定义可知等边三角形的三条边都相等，这是研究等边三角形的基础．
例　等腰三角形一边长为1，周长为5，那么这个三角形的腰长是多少？
错答：①若底边为1，则腰长为 ②若腰长为1；所以腰长为1或2.
正答：①若底边为1，腰长为 且2，2，1满足三角形的三边关系；
②若腰长为1，而1，1，3三边不满足三角形的三边关系；所以这个三角形的腰长为2.
错因：求出等腰三角形边长后忽略了三角形的三边关系．