2.5　逆命题和逆定理课件

课件7张PPT。第2章　特殊三角形2.5　逆命题和逆定理逆命题、互逆命题、逆定理、互逆定理例1　下列定理，有没有逆定理？若有，请说出其逆定理．
(1)全等三角形的对应角相等．
(2)有一个角等于60°的等腰三角形是等边三角形．分析：先写出定理的逆命题，然后再判断逆命题的正确性．如果逆命题正确，说明原定理有逆定理；如果逆命题错误，说明原定理有逆命题但没有逆定理．
解：(1)没有逆定理．
(2)有逆定理，逆定理为：等边三角形是有一个角等于60°的等腰三角形．
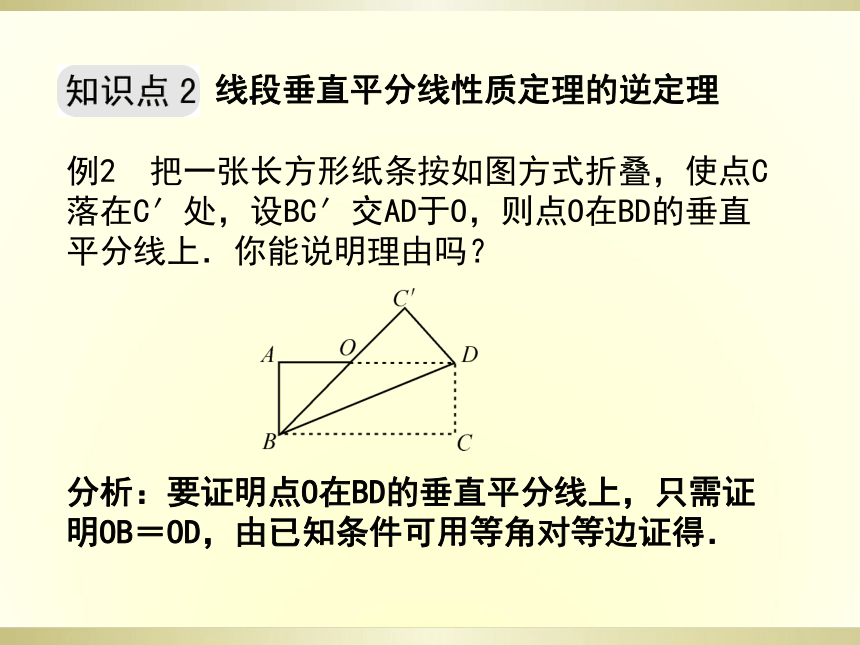
注意点：写逆命题(逆定理)的关键在于明确原命题的条件和结论分别是什么，在写逆命题时要求完整、准确．线段垂直平分线性质定理的逆定理例2　把一张长方形纸条按如图方式折叠，使点C落在C′处，设BC′交AD于O，则点O在BD的垂直平分线上．你能说明理由吗？
分析：要证明点O在BD的垂直平分线上，只需证明OB＝OD，由已知条件可用等角对等边证得．解：∵AD∥BC　
∴∠CBD＝∠ADB　
又∵∠CBD＝∠C′BD　
∴∠C′BD＝∠ADB　
∴OB＝OD　
∴点O在BD的垂直平分线上．
注意点：要证一点在线段的垂直平分线上，只要说明这个点到这条线段的两个端点的距离相等即可，这是线段垂直平分线性质定理的逆定理最重要的使用．例1　下列说法：①若原命题是真命题，则逆命题是真命题；②若原命题是假命题，则逆命题也是假命题；③每个命题都有逆命题；④每个定理都有逆定理．正确的结论有(　　)
A．1个 B．2个
C．3个 D．4个
错答：D正答：A
错因：对逆命题、逆定理的概念理解不透彻，以为每个命题都有逆命题，那么每个定理也都有逆定理了．并且混淆了命题的真假，以为逆命题的真假由原命题真假决定．
例2　说出“等腰三角形两底角相等”的逆命题．
错答：两底角相等的三角形为等腰三角形．
正答：有两个角相等的三角形为等腰三角形．
错因：没有理解清楚等腰三角形概念，当写出底角时，三角形已经为等腰三角形了．有些问题条件、结论位置互换时要注意专有名词的使用正确．