2.7　探索勾股定理(第1课时)课件

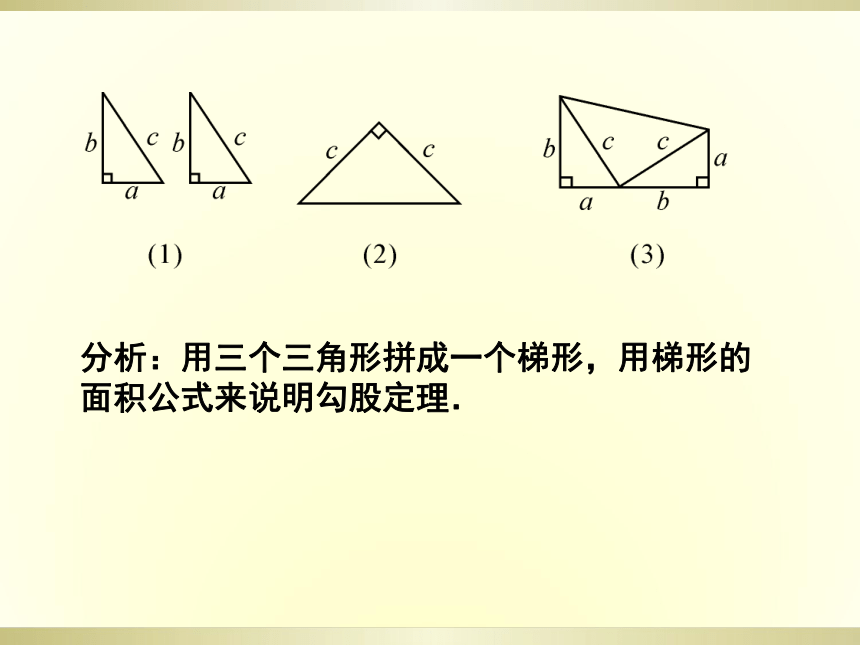
课件8张PPT。第2章　特殊三角形2.7　探索勾股定理(第1课时)勾股定理的探索例1　如图(1)所示，用硬纸板做成两个全等的直角三角形，两直角边长分别为a，b，斜边长为c.图(2)是腰长为c的等腰直角三角形，请你开动脑筋，将它们拼成一个能说明勾股定理的图形．画出拼成的图形的示意图，并用其说明勾股定理．
分析：用三个三角形拼成一个梯形，用梯形的面积公式来说明勾股定理．
解：如图(3)所示，用三个直角三角形拼成一个直角梯形．
三个直角三角形的面积和为
直角梯形的面积为 　
∴ 　 化简得a2＋b2＝c2，
即勾股定理成立．
注意点：拼图法可以用来说明解决一些代数式恒等的问题，使用过程中要注意两点：(1)一般通过割补、拼接，用相同的材料得到不同的(或同一个)图形；(2)用拼成的不同(或同一个)图形的面积之间的关系可以建立代数式的恒等关系．例2　如图所示，在△ABC中，AB＝13，BC＝14，AC＝15，求BC边上的高线AD.
分析：要求出AD需先求出BD或CD，由于DB＋CD＝BC，所以可设DB＝x，则CD＝14－x，这样分别在两个直角三角形中根据勾股定理把AD2用含x的代数式表示出来，然后得到关于x的方程，求出x即可解决问题．解：设DB＝x，则CD＝14－x.
在Rt△ABD中，由勾股定理得AD2＋x2＝132，∴AD2＝132－x2
同理可得在Rt△ACD中，AD2＝152－(14－x)2
∴132－x2＝152－(14－x)2　解得x＝5，即BD＝5.
∴ 　
∴BC边上的高线AD为12.
注意点：运用勾股定理建立方程，通过方程思想，解决一些几何问题，在一些几何计算中运用比较多．
变式：如图，折叠长方形的一边AD，使点D落在BC边上的点F处，折痕与CD边交于点E.已知AB＝8cm，BC＝10cm，求CE的长．
解：由折叠的性质可得，AD＝AF＝10，
DE＝EF.在Rt△ABF中，
∵AD＝AF＝10，AB＝8，
∴ 　
∴CF＝BC－BF＝10－6＝4
在Rt△CEF中，设CE＝x，则EF＝DE＝8－x.
由勾股定理得
x2＋42＝(8－x)2，解得x＝3，
∴CE的长为3cm.例　现有两条线段的长分别是4cm和5cm，再取一条线段组成一个直角三角形，那么所取线段的长度是多少？
错答：所取的第三条线段的长为
正答：若第三边为直角边，则第三边为
若第三边为斜边，则第三边为
所以第三条线段的长为3cm和
错因：由于思维定势只考虑了3，4，5的情况，没有对哪一条是斜边进行分类讨论．