2.8　直角三角形全等的判定课件

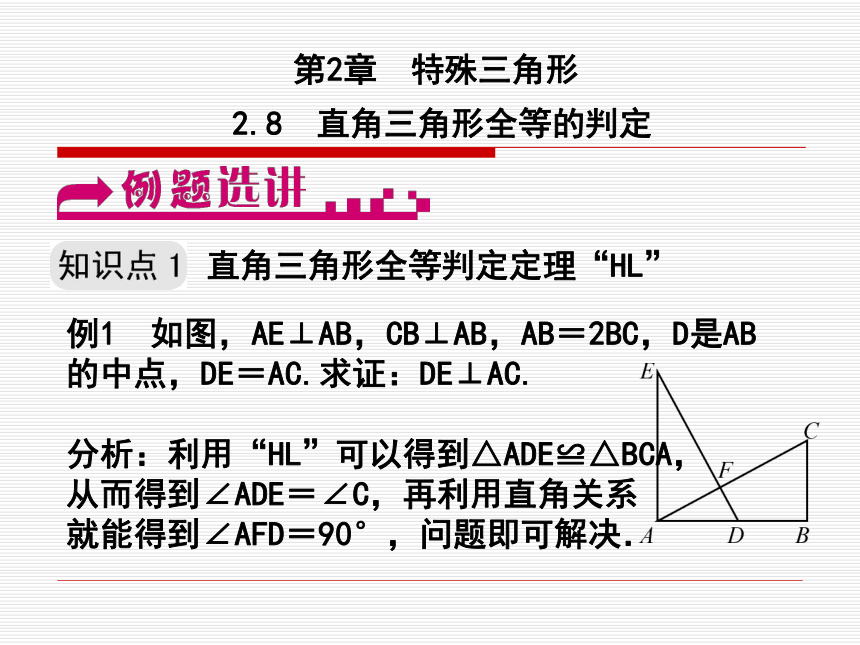
课件8张PPT。第2章　特殊三角形2.8　直角三角形全等的判定直角三角形全等判定定理“HL”例1　如图，AE⊥AB，CB⊥AB，AB＝2BC，D是AB的中点，DE＝AC.求证：DE⊥AC.
分析：利用“HL”可以得到△ADE≌△BCA，
从而得到∠ADE＝∠C，再利用直角关系
就能得到∠AFD＝90°，问题即可解决．证明：∵AE⊥AB，CB⊥AB　∴∠EAD＝∠ABC＝90°，∵D是AB的中点，AB＝2BC　∴AD＝BC，
在Rt△ADE和Rt△BCA中，
∴Rt△ADE≌Rt△BCA(HL)　
∴∠ADE＝∠C　
∵∠CAB＋∠C＝90°　
∴∠CAB＋∠ADE＝90°　
∴∠AFD＝90°，即DE⊥AC.
注意点：当两个直角三角形全等后，往往要用到同角(等角)的余角相等这些结论来说明问题，使用过程中要注意角的转换．变式：如图，在等腰Rt△ABC中，∠ACB＝90°，点D是斜边AB上任一点，AE⊥CD，垂足为E，BF⊥CD交CD的延长线于点F，CH⊥AB，垂足为H，交AE于点G.问：BD与CG相等吗？请说明理由．
证明：∵∠ACB＝90°，AE⊥CD　
∴∠CAE＋∠ACE＝90°，∠ACE＋∠BCE＝90°，∴∠CAE＝∠BCE
∵BF⊥CD　
∴∠CFB＝90°　∴∠AEC＝∠CFB，
又∵AC＝CB　
∴△ACE≌△CBF(AAS)　
∴CE＝BF，
∵CH⊥AB，BF⊥CF　
∴∠HCD＋∠CDH＝90°，∠DBF＋∠BDF＝90°，∵∠CDH＝∠BDF　
∴∠HCD＝∠DBF　
∴△CEG≌△BFD(ASA)，∴BD＝CG.角平分线性质定理的逆定理例2　已知：如图所示，BE＝CF，BF⊥AC于点F，CE⊥AB于点E，BF和CE交于点D.证明：AD平分∠BAC.
分析：由于BF⊥AC，CE⊥AB，只要DE＝DF即可证明AD平分∠BAC.DE＝DF可以由△BDE≌△CDF得到．证明：∵BF⊥AC，CE⊥AB　
∴∠DEB＝∠DFC＝90°.
在△BDE和△CDF中，
∴△BDE≌△CDF(AAS)　
∴DE＝DF　又∵DE⊥AB，DF⊥AC　
∴AD平分∠BAC.
注意点：要说明一条射线是某个角的平分线，可以说明射线上一点到这个角的两边距离相等．在解题过程中要注意垂直关系的书写，指明垂线段，并由垂线段相等直接得到两个角相等(或某射线是角的平分线)．例　下列说法不正确的是(　　)
A．有一锐角和一边对应相等的两个直角三角形全等
B．有两直角边对应相等的两个直角三角形全等
C．有两角对应相等的两个直角三角形全等
D．有两边对应相等的两个直角三角形全等
错答：D
正答：C
错因：对直角三角形全等的判定定理理解错误，没有注意到分两种情况：一种两直角边和直角用SAS证明全等，另一种直角边和斜边用HL证明全等．