2.1图形的轴对称同步训练

2.1图形的轴对称
　
一．选择题（共8小题）
1．在平面直角坐标系中，已知点A的坐标是（2，3），点B的坐标是（1，0），点C是点A关于点B的对称点，则点C的坐标是（　　）21世纪教育网版权所有
A．（2，﹣3） B．（﹣2，﹣3） C．（0，﹣2） D．（0，﹣3）
2．用矩形纸片折出直角的平分线，下列折法正确的是（　　）
A． B． C． D．
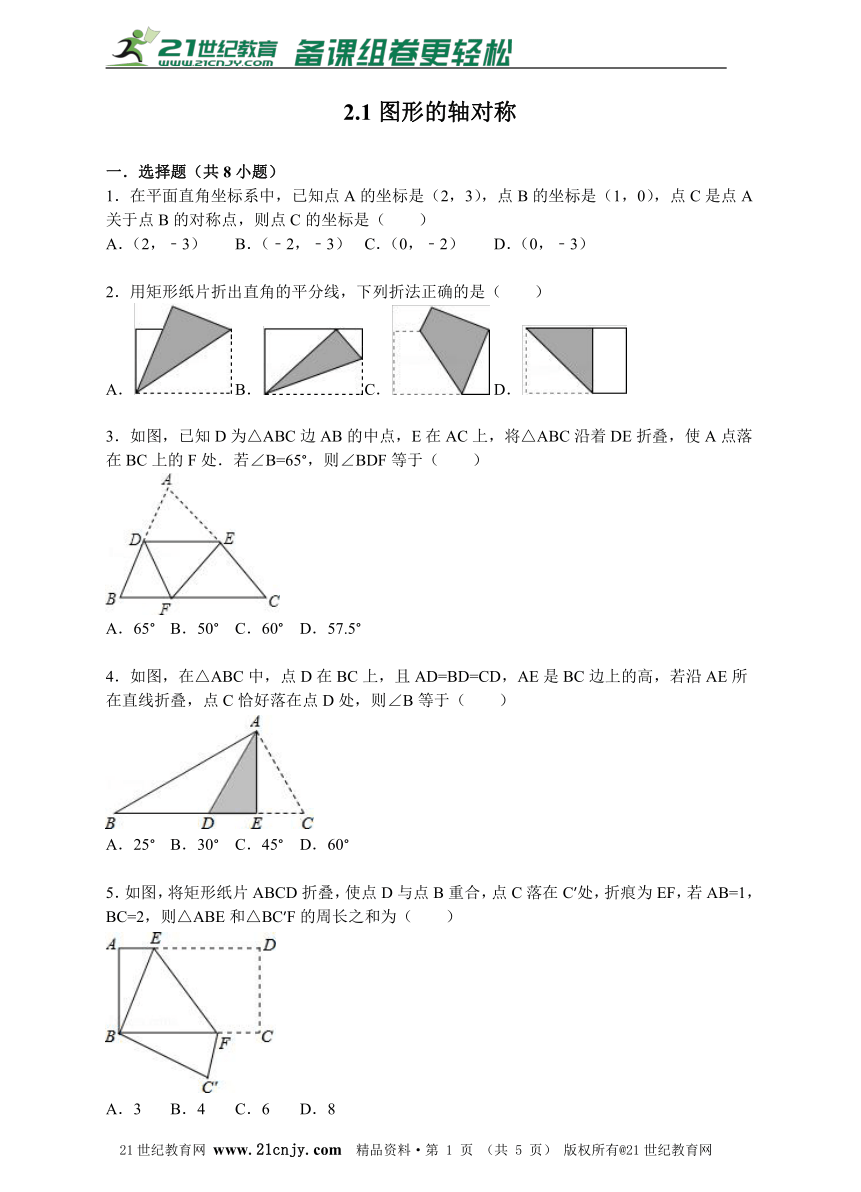
3．如图，已知D为△ABC边AB的中点，E在AC上，将△ABC沿着DE折叠，使A点落在BC上的F处．若∠B=65°，则∠BDF等于（　　）21教育网
A．65° B．50° C．60° D．57.5°
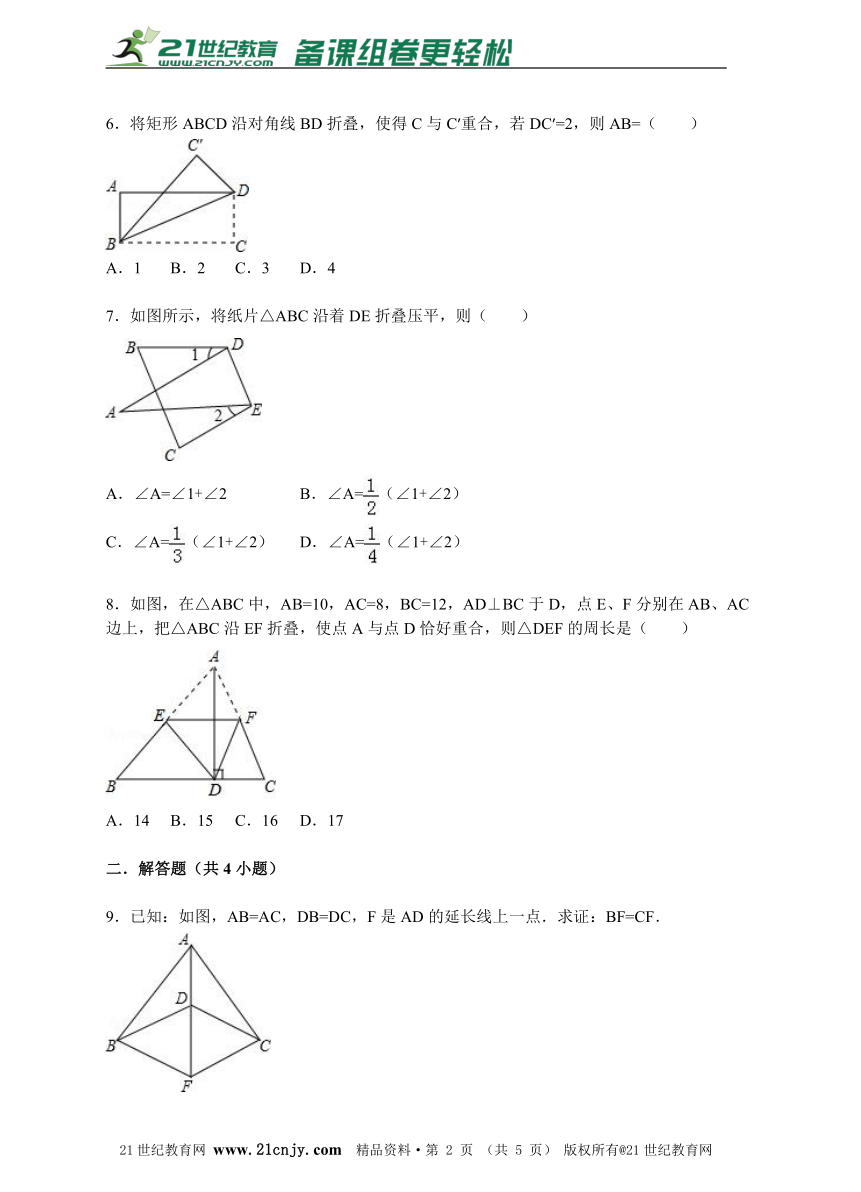
4．如图，在△ABC中，点D在BC上，且AD=BD=CD，AE是BC边上的高，若沿AE所在直线折叠，点C恰好落在点D处，则∠B等于（　　）21cnjy.com
A．25° B．30° C．45° D．60°
5．如图，将矩形纸片ABCD折叠，使点D与点B重合，点C落在C′处，折痕为EF，若AB=1，BC=2，则△ABE和△BC′F的周长之和为（　　）21·cn·jy·com
A．3 B．4 C．6 D．8
6．将矩形ABCD沿对角线BD折叠，使得C与C′重合，若DC′=2，则AB=（　　）
A．1 B．2 C．3 D．4
7．如图所示，将纸片△ABC沿着DE折叠压平，则（　　）
A．∠A=∠1+∠2 B．∠A=（∠1+∠2）
C．∠A=（∠1+∠2） D．∠A=（∠1+∠2）
8．如图，在△ABC中，AB=10，AC=8，BC=12，AD⊥BC于D，点E、F分别在AB、AC边上，把△ABC沿EF折叠，使点A与点D恰好重合，则△DEF的周长是（　　）
A．14 B．15 C．16 D．17
　
二．解答题（共4小题）
9．已知：如图，AB=AC，DB=DC，F是AD的延长线上一点．求证：BF=CF．
10．如图，AB平分∠CAD，AC=AD，求证：BC=BD；
11．如图，在△ABD和△ACD中，有四个判断：①AB=AC；②∠1=∠2；③∠B=∠C；④BD=CD．请你从中选出三个判断，其中两个作为题设、一个作为结论，组成一个真命题．（要求写出已知、求证及证明过程）www.21-cn-jy.com
12．我们把两组邻边分别相等的四边形叫做“筝形”．如图，四边形ABCD是一个筝形，其中AB=CB，AD=CD，请你写出与筝形ABCD的角或者对角线有关的一个结论，并证明你的结论．2·1·c·n·j·y
　

2.1图形的轴对称
参考答案与试题解析
　
一．选择题（共8小题）
2．解：A．当长方形如A所示对折时，其重叠部分两角的和中，一个顶点处小于90°，另一顶点处大于90°，故A错误；【来源：21·世纪·教育·网】
B．当如B所示折叠时，其重叠部分两角的和小于90°，故B错误；
C．当如C所示折叠时，折痕不经过长方形任何一角的顶点，所以不可能是角的平分线，故C错误；
D．当如D所示折叠时，两角的和是90°，由折叠的性质可知其折痕必是其角的平分线，故D正确．
故选：D．
　
　
5．解：将矩形纸片ABCD折叠，使点D与点B重合，点C落在C′处，折痕为EF，
由折叠特性可得，CD=BC′=AB，∠FC′B=∠EAB=90°，∠EBC′=∠ABC=90°，
∵∠ABE+∠EBF=∠C′BF+∠EBF=90°∴∠ABE=∠C′BF
在△BAE和△BC′F中，，
∴△BAE≌△BC′F（ASA），
∵△ABE的周长=AB+AE+EB=AB+AE+ED=AB+AD=1+2=3，
△ABE和△BC′F的周长=2△ABE的周长=2×3=6．
　
6．解：在矩形ABCD中，CD=AB，∵矩形ABCD沿对角线BD折叠后点C和点C′重合，
∴C′D=CD，∴C′D=AB，∵DC′=2，∴AB=2．故选：B．
　
7．解：根据折叠及邻补角的性质，得
∠1=180°﹣2∠ADE，∠2=180°﹣2∠AED，
∴∠1+∠2=360°﹣2（∠ADE+∠AED），
∴∠ADE+∠AED=[360°﹣（∠1+∠2）]=180°﹣（∠1+∠2），
∴在△ADE中，由内角和定理，得
∠A=180°﹣（∠ADE+∠AED）=180°﹣180°+（∠1+∠2）=（∠1+∠2）．故选B．
　
8．解：由折叠的性质可得，△AEF≌△DEF，EF为△ABC的中位线，
∵AB=10，AC=8，BC=12，
∴AE=ED=5，AF=FC=4，EF=6，
∴△DEF的周长=5+4+6=15．故选B．
　
二．解答题（共4小题）
9．证明：∵在△ABD和△ACD中
∴△ABD≌△ACD，∴∠BAD=∠CAD，
在△BAF和△CAF中∴△BAF≌△CAF（SAS），∴BF=CF．
10．证明：∵AB平分∠CAD，∴∠CAB=∠DAB，
在△ABC和△ABD中∴△ABC≌△ABD（SAS），∴BC=BD．