3.5圆周角（1）课件

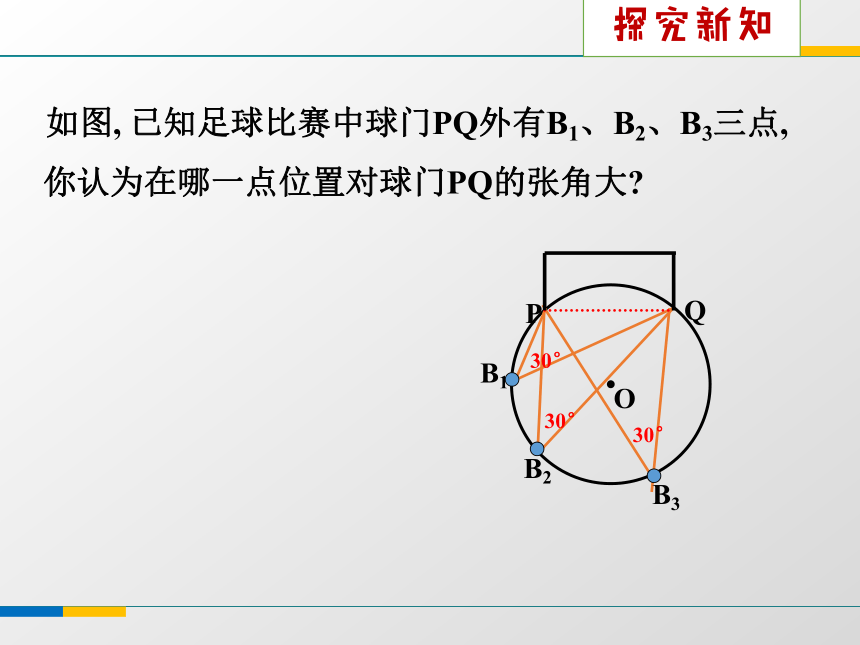
课件22张PPT。3.5　圆周角（1）B1B3B2 如图, 已知足球比赛中球门PQ外有B1、B2、B3三点,30°30°30°你认为在哪一点位置对球门PQ的张角大?
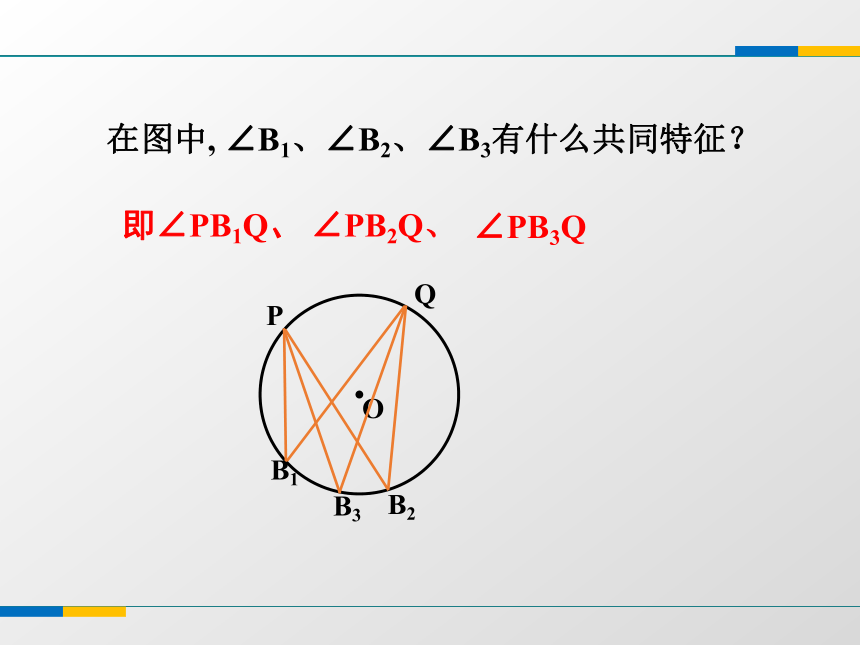
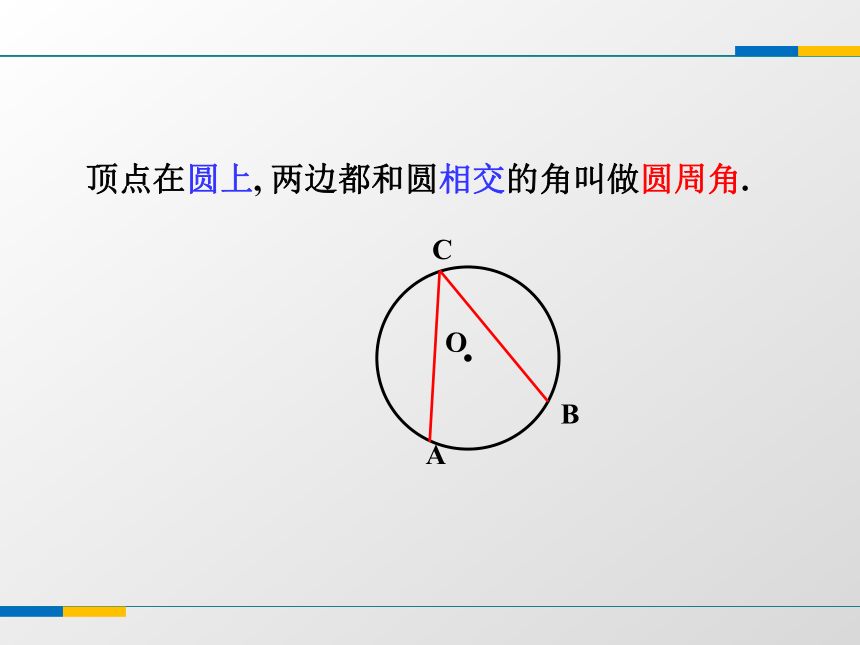
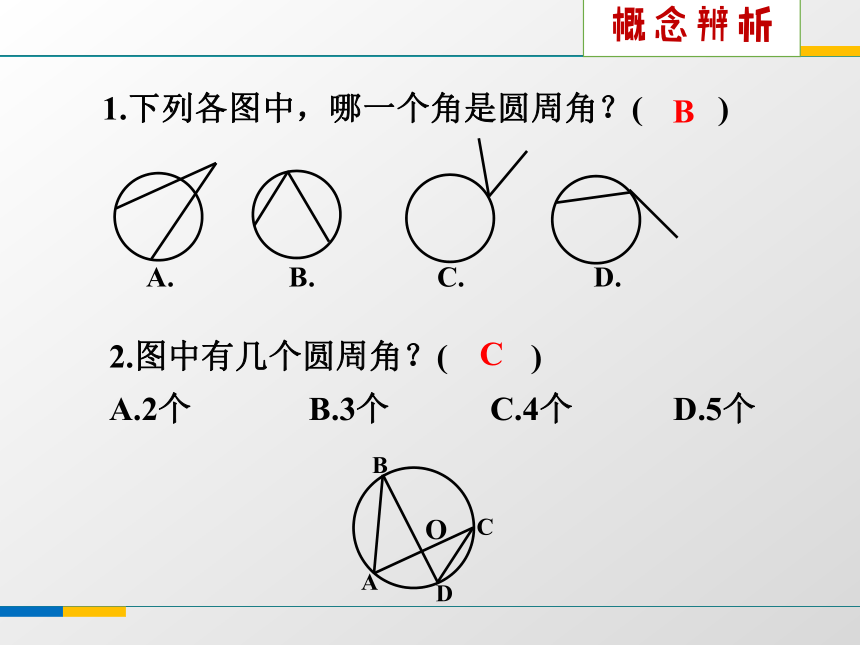
探究新知在图中, ∠B1、∠B2、∠B3有什么共同特征？ 　即∠PB1Q、∠PB2Q、∠PB3Q顶点在圆上, 两边都和圆相交的角叫做圆周角.1.下列各图中，哪一个角是圆周角？( )2.图中有几个圆周角？( )
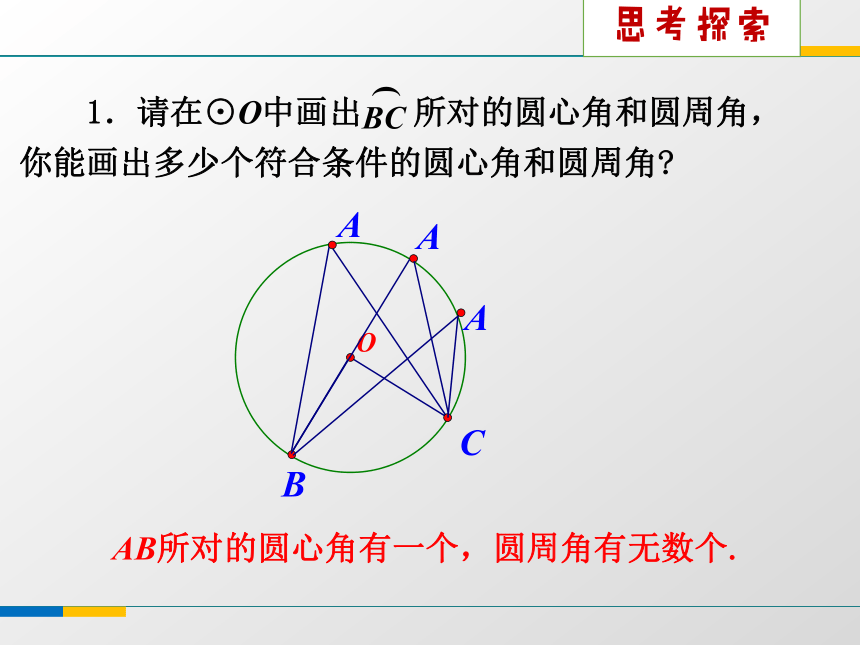
A.2个 B.3个 C.4个 D.5个 BC概念辨析OBCA　　1．请在⊙O中画出 所对的圆心角和圆周角，
你能画出多少个符合条件的圆心角和圆周角?
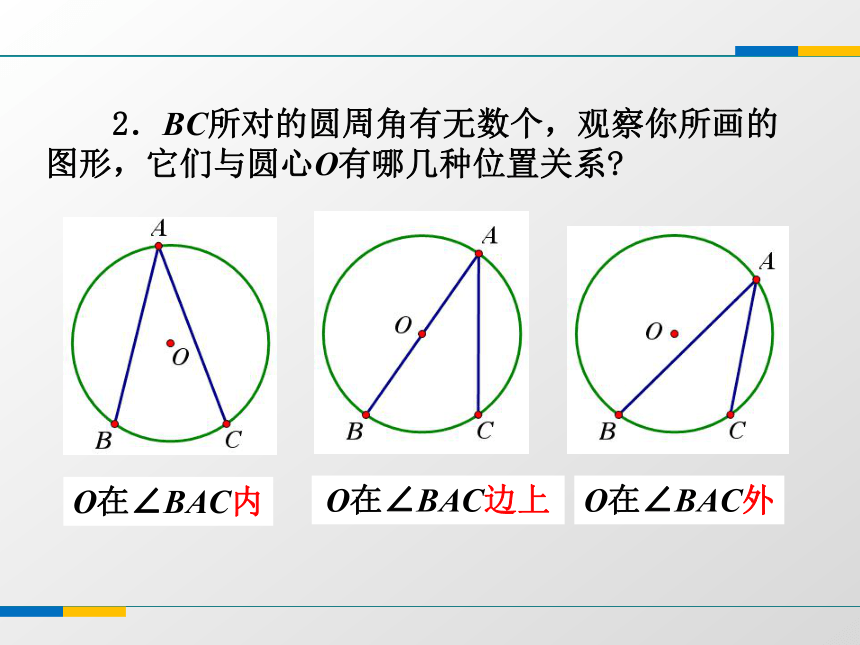
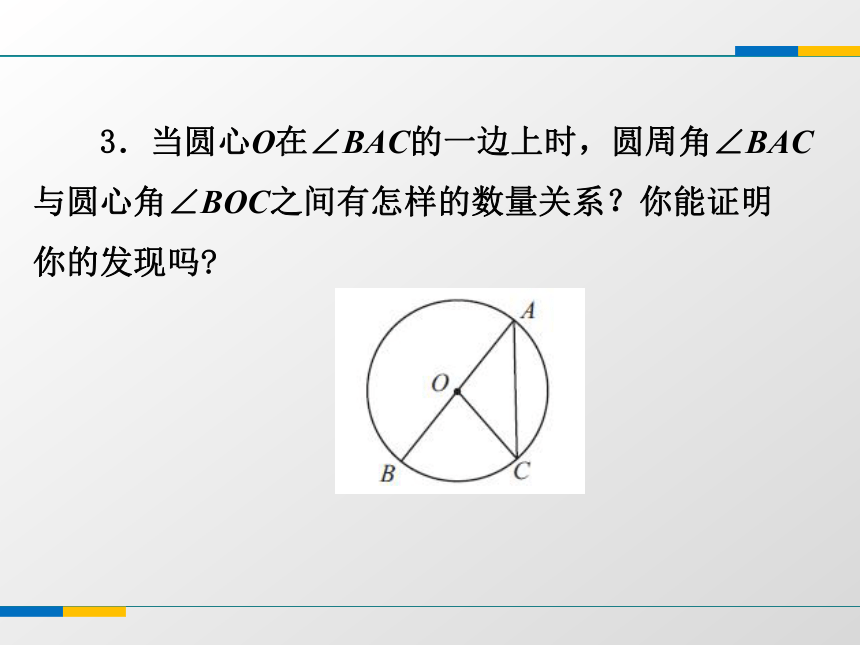
　AB所对的圆心角有一个，圆周角有无数个.AA思考探索　　2．BC所对的圆周角有无数个，观察你所画的图形，它们与圆心O有哪几种位置关系?O在∠BAC内O在∠BAC边上O在∠BAC外　　3．当圆心O在∠BAC的一边上时，圆周角∠BAC
与圆心角∠BOC之间有怎样的数量关系？你能证明
你的发现吗?∵∠BOC是△AOC的外角，
∴∠BOC＝∠A ＋∠C.
∵OA＝OC ，
∴∠C＝∠A .
∴∠BOC＝2∠A .即证明：探索证明5．当圆心O在∠BAC的内部或外部时， 的关系还成立吗? 证明：作直径AD．∵∴即 同弧所对的圆周角相等，都等于该弧所对圆心角的一半.　　问题1　如图1，BC是⊙O的直径，A是⊙O上任一点，你能确定∠BAC的度数吗?图1∠BAC＝90o问题探究　　问题2　如图2，圆周角∠BAC＝90o，弦BC经过圆心O吗？为什么？圆周角定理的推论：半圆（或直径）所对的圆周角是直角；用于判断某个圆周角是否是直角用于判断某条弦是否是直径90°的圆周角所对的弦是直径．例1 如图，点A、B、D、E在⊙O上，弦AE、BD的延长线相交于点C. 若AB是⊙O的直径，D是BC的中点．
(1) 试判断AB、AC之间的大小关系，并给出证明；
(2) 在上述题设条件下，△ABC还需满足什么条件，点E才一定是AC的中点？(直接写出结论)解：(1) AB＝AC，
证明：连结AD
∵ AB是⊙O的直径
∴ ∠ADB＝∠ADC＝90°
又∵AD为公共边，BD＝DC
∴ Rt△ABD≌Rt△ACD
∴ AB＝AC例题探究解： (2)△ABC为正三角形或AB＝BC或AC＝BC或∠A＝∠B或∠A＝∠C等．例1 如图，点A、B、D、E在⊙O上，弦AE、BD的延长线相交于点C. 若AB是⊙O的直径，D是BC的中点．
(1) 试判断AB、AC之间的大小关系，并给出证明；
(2) 在上述题设条件下，△ABC还需满足什么条件，点E才一定是AC的中点？(直接写出结论)1. 如图，已知⊙O中半径OA⊥OB，弦AC⊥BD于点E，你能发现AD和BC有怎样的位置关系吗？为什么？解：AD和BC的位置关系是AD∥BC. 理由如下：
∵OA⊥OB，∴∠AOB＝90°
∴∠D＝∠C＝45°
∵AC⊥BD于点E
∴∠BEC＝90°
又∵∠C＝45°，∴∠EBC＝45°
∴∠D＝∠EBC
∴ AD∥BC课堂练习2. 如图，在⊙O中，直径AB⊥CD于点E，连结CO并延长交AD于点F，且CF⊥AD. 求∠D的度数．解：连结BD.
∵AB是⊙O的直径，∴BD⊥AD
又∵CF⊥AD
∴BD∥CF，∴∠BDC＝∠C.
又∵∠BDC＝∠BOC, ∴∠C＝∠BOC.
∵AB⊥CD，即∠OEC＝90°
∴∠C＋∠BOC＝90°
∴∠C＝30°
∴∠ADC＝90°－∠C＝60°.　　这节课你有哪些收获和困惑？课堂小结1、圆周角的定义：2、圆周角定理：顶点在圆上，两边都与圆相交的角. 一条弧所对的圆周角等于它所对的圆心角的一半.3、圆周角定理的推论： 半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径.课本作业题A组必做，
B组选做.课后作业