3.6《圆内接四边形》课件(共16张PPT)
文档属性
| 名称 | 3.6《圆内接四边形》课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 881.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-27 18:56:35 | ||
图片预览




文档简介
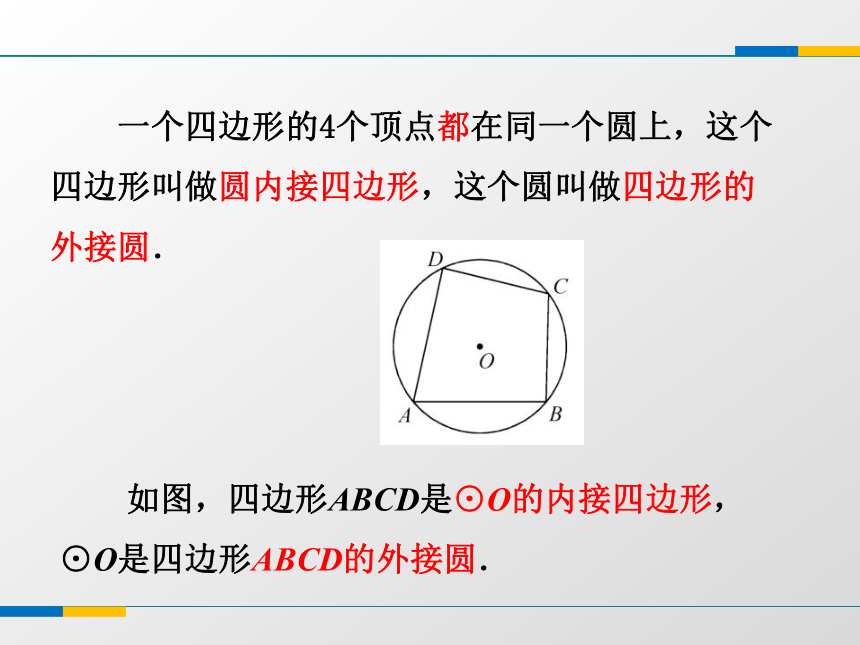
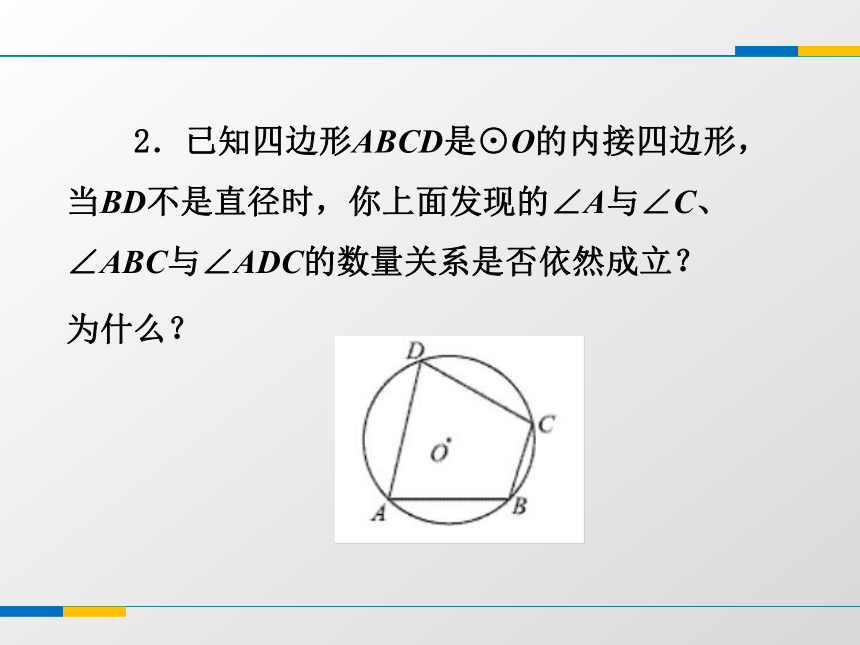
课件16张PPT。3.6 圆内接四边形 1.过三角形的三个顶点能画一个圆吗?为什么?回顾探究 不在同一条直线上的三点确定一个圆. 2.过四边形的四个顶点能画一个圆吗?为什么?不一定 一个四边形的4个顶点都在同一个圆上,这个四边形叫做圆内接四边形,这个圆叫做四边形的外接圆. 如图,四边形ABCD是⊙O的内接四边形,⊙O是四边形ABCD的外接圆. 1.已知四边形ABCD是⊙O的内接四边形,当BD是直径时,你能发现∠A与∠C、∠ABC与∠ADC有怎样的数量关系?为什么?问题探究 2.已知四边形ABCD是⊙O的内接四边形,当BD不是直径时,你上面发现的∠A与∠C、∠ABC与∠ADC的数量关系是否依然成立?
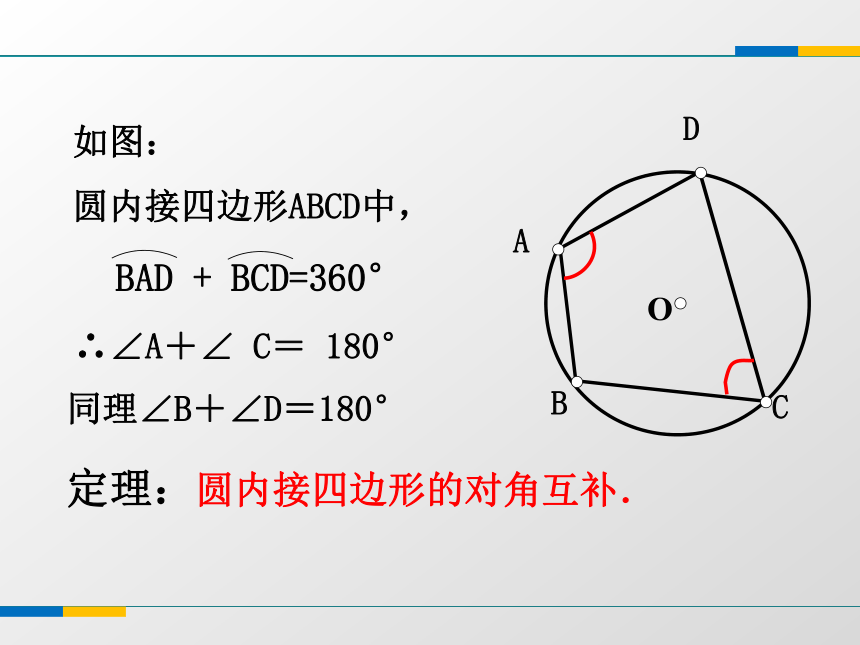
为什么?如图:
圆内接四边形ABCD中,∴∠A+∠ C= 180°同理∠B+∠D=180°定理:圆内接四边形的对角互补.四边形ABCD内接于⊙O,则∠A+∠C=______
∠B+∠ADC=_______;
若∠B=80°,
则∠ADC=______ ,
∠CDE=_________.180°180°100°80°做一做例题探究例1 如图,△ABC的外角平分线AD交外接圆于D,求证:DB=DC.解:∵ AD是∠EAC的平分线∴∠DAC=∠DAE
∵ 四边形ABCD内接于圆
∴∠DCB=∠DAE
∵ 圆周角∠DBC和∠DAC所对的弧都是CD
∴∠DBC=∠DAC
∴∠DBC=∠DCB
∴ DB=DC例2 如果要把直径为30cm的圆柱形原木锯成一根横截面为正方形的木材,并使截面尽可能地大,应怎样锯?最大横截面面积是多少?如果这根原木长15m,问锯出的木材的体积为多少立方米(树皮等损耗略去不计)?解:如图,所得的四边形是矩形,理由如下:∵AC,BD是⊙O的直径∴AO=OC=OB=OD∴四边形ABCD是平行四边形又∵AC=BD∴四边形ABCD是矩形当AC⊥BD时,四边形ABCD是正方形∵AC=BD=30cm∴AO=BO=15cm∴S正方形ABCD=15×15÷2×4=450(cm2)=4.5×10-2(m2)∴V=4.5×10-2×15=0.675(m3) 1.已知:图中,四边形ABCD为⊙O的内接四边形,E为AB延长线上一点,且∠AOC=80 °,则 ∠D= ,∠CBE= . 课堂练习40°40° 2.圆内接四边形ABCD中,∠A:∠B:∠C:∠D=2:4:7:m ,则m= ,∠D= .5100°解:设∠A、∠B、∠C的度数分别对于2x、3x、6x,3.在圆内接四边形ABCD中, ∠A、∠B、 ∠C的度数之比是2︰3︰6. 求这个四边形各角的度数.由于四边形ABCD内接于圆,∴ ∠A+ ∠C=∠B+∠D=180°∵ 2x+6x=180°∴ x=22.5°∴ ∠A=45°, ∠B=67.5°, ∠C =135°
∠D=180°-67.5°=112.5°.这节课你有哪些收获?课堂小结1.定义:
一个四边形的4个顶点都在同一个圆上,这个四边形叫做圆内接四边形,这个圆叫做四边形的外接圆. 2.定理:
圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角.课本作业题A组课后作业
为什么?如图:
圆内接四边形ABCD中,∴∠A+∠ C= 180°同理∠B+∠D=180°定理:圆内接四边形的对角互补.四边形ABCD内接于⊙O,则∠A+∠C=______
∠B+∠ADC=_______;
若∠B=80°,
则∠ADC=______ ,
∠CDE=_________.180°180°100°80°做一做例题探究例1 如图,△ABC的外角平分线AD交外接圆于D,求证:DB=DC.解:∵ AD是∠EAC的平分线∴∠DAC=∠DAE
∵ 四边形ABCD内接于圆
∴∠DCB=∠DAE
∵ 圆周角∠DBC和∠DAC所对的弧都是CD
∴∠DBC=∠DAC
∴∠DBC=∠DCB
∴ DB=DC例2 如果要把直径为30cm的圆柱形原木锯成一根横截面为正方形的木材,并使截面尽可能地大,应怎样锯?最大横截面面积是多少?如果这根原木长15m,问锯出的木材的体积为多少立方米(树皮等损耗略去不计)?解:如图,所得的四边形是矩形,理由如下:∵AC,BD是⊙O的直径∴AO=OC=OB=OD∴四边形ABCD是平行四边形又∵AC=BD∴四边形ABCD是矩形当AC⊥BD时,四边形ABCD是正方形∵AC=BD=30cm∴AO=BO=15cm∴S正方形ABCD=15×15÷2×4=450(cm2)=4.5×10-2(m2)∴V=4.5×10-2×15=0.675(m3) 1.已知:图中,四边形ABCD为⊙O的内接四边形,E为AB延长线上一点,且∠AOC=80 °,则 ∠D= ,∠CBE= . 课堂练习40°40° 2.圆内接四边形ABCD中,∠A:∠B:∠C:∠D=2:4:7:m ,则m= ,∠D= .5100°解:设∠A、∠B、∠C的度数分别对于2x、3x、6x,3.在圆内接四边形ABCD中, ∠A、∠B、 ∠C的度数之比是2︰3︰6. 求这个四边形各角的度数.由于四边形ABCD内接于圆,∴ ∠A+ ∠C=∠B+∠D=180°∵ 2x+6x=180°∴ x=22.5°∴ ∠A=45°, ∠B=67.5°, ∠C =135°
∠D=180°-67.5°=112.5°.这节课你有哪些收获?课堂小结1.定义:
一个四边形的4个顶点都在同一个圆上,这个四边形叫做圆内接四边形,这个圆叫做四边形的外接圆. 2.定理:
圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角.课本作业题A组课后作业
同课章节目录
