2.1等腰三角形

教 案(总第 课时)
课 题 2.1等腰三角形 课型 新授 设计者 李飞君
日 期 200 年 月 日 第 节 教具
教 学 目 标 1．使学生了解等腰三角形的有关概念 。2．通过探索等腰三角形的性质，使学生掌握等腰三角形的轴对称性。进一步经历观察、实验、推理、交流等活动。3．了解本节知识在现实生活中的应用，增强审美意识，学会发现生活中处处可见的对称美。
重 点 难 点 重点：等腰三角形轴对称性质。难点：利用等腰三角形的有关知识进行分析说理，分类思想解决等腰三角形的有关问题。
教学内容 教学过程 修正案
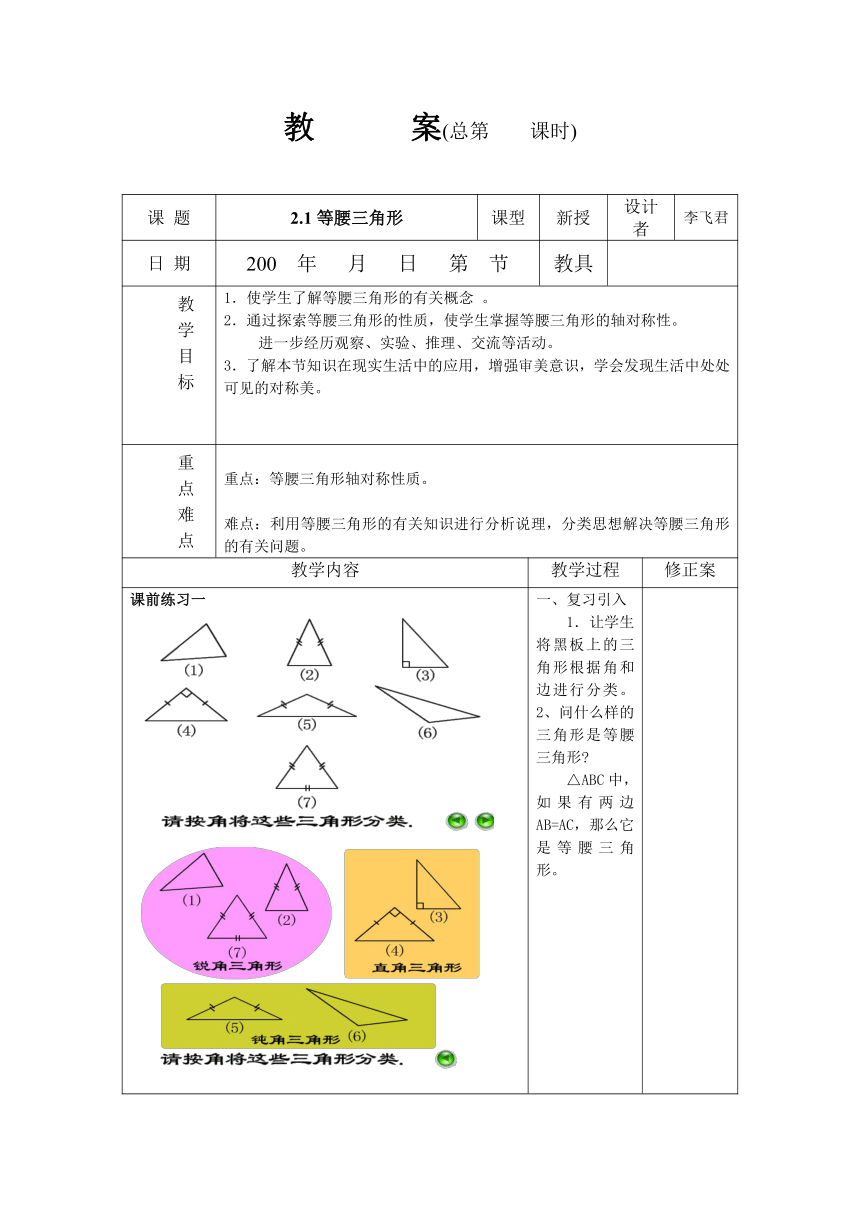
课前练习一 一、复习引入 1．让学生将黑板上的三角形根据角和边进行分类。2、问什么样的三角形是等腰三角形 △ABC中，如果有两边AB=AC，那么它是等腰三角形。
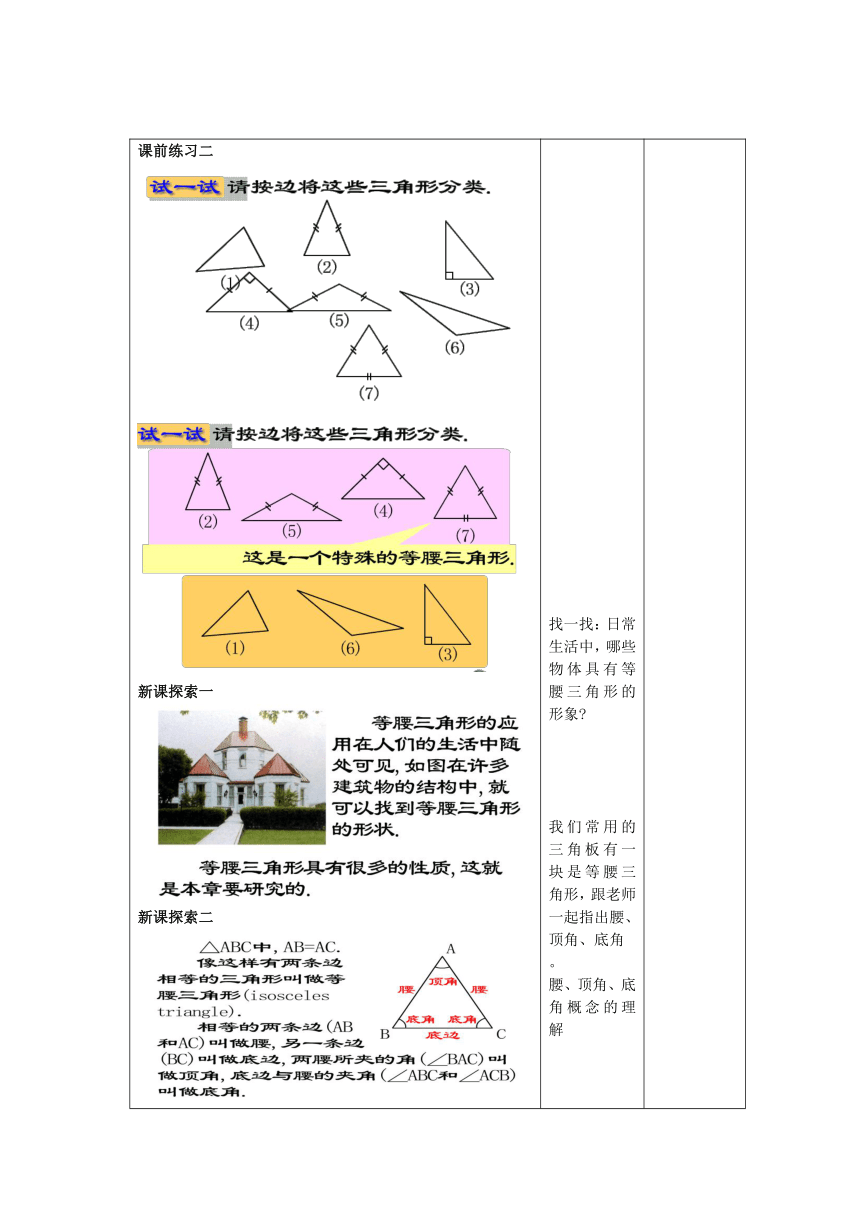
课前练习二新课探索一新课探索二 找一找：日常生活中，哪些物体具有等腰三角形的形象 我们常用的三角板有一块是等腰三角形，跟老师一起指出腰、顶角、底角。腰、顶角、底角概念的理解
新课探索三新课探索四课内练习一课内练习二 实验。 现在请同学们依着操作要求做一张等腰三角形，你能发现什么现象吗 请你尽可能多的写出结论。它是怎样的一个图形？----轴对称图形它的对称轴是什么？-------顶角平分线所在的直线是它的对称轴例题精讲引导：将等腰三角形ABC沿顶角平分线折叠时，线段AD与AE能重合吗？为什么？边AB与AC呢？2．说明点D与点E，点B与点C分别有怎样的位置关系？3．轴对称图形有什么性质？由此可推出AP与DE，BC有怎样的位置关系？那么DE与BC呢？
课内练习三课内练习四课内练习五本课小结布置作业 基础知识巩固： （补充） 填空：在△ABC中，AB＝AC，D在BC上， 1．如果AD⊥BC，那么∠BAD＝∠______，BD＝_______ 2．如果∠BAD＝∠CAD，那么AD⊥_____，BD＝______ 3．如果BD＝CD，那么∠BAD＝∠_______，AD⊥______小结 本节课，我们学习了等腰三角形的轴对称性质。大家想一想，怎样用此性质来解决点与点，线与线之间的位置关系？说说你的想法。
拓展练习一