一元一次方程复习

(共52张PPT)
数学庄园欢乐行
欢迎你们到数学庄园来！但进入这个庄园可不那么简单哟！可是先要考考你们的哦！
列方程解应用题的一般步骤
1、审题：分析题意，找出题中关键词及数量关系。
2、设元：选择一个适当的未知数用字母表示。
3、列方程：根据等量关系列出方程；
4、解方程，求出未知数的值；
5、检验并作答：检验求得的值是否正确、合理；写 出答案。
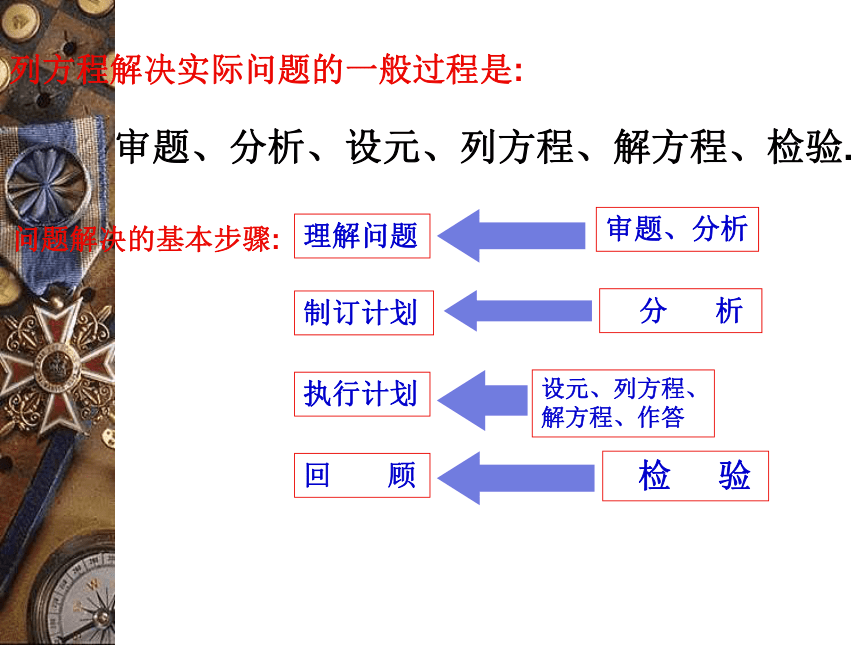
列方程解决实际问题的一般过程是:
审题、分析、设元、列方程、解方程、检验.
理解问题
制订计划
执行计划
问题解决的基本步骤:
回 顾
审题、分析
分 析
设元、列方程、解方程、作答
检 验
一填空题
1、一个数x的2倍减去7的差, 得36 ,列方程为____________；
2、方程5 x – 6 = 0的解是x =________；
3、 方程去分母得： .
热身练习
2x-7=36
1.2
5x-10 = -x+1
4、一根长18米的铁丝围成一个长是宽
的2倍的长方形,这个长方形的面积为
；
18平方米
5
4
60
480
14.4
设兔有x只，列方程为：
4x+2（9-x）=26
6、小明每秒钟跑4米，则他15秒钟跑___米,2分钟跑______米,1小时跑_____千米.
5、鸡兔同笼共9只，腿26条, 则鸡_____只，兔_____只；
7、小明每秒钟跑6米，小彬每秒钟跑5米，小彬站在小
明前10米处，两人同时起跑，小明多少秒钟追上
小彬 --------------------------------------------（ ） A 5秒， B 6秒， C 8秒， D 10秒；
D
例1、日历中2×2方块的四个数的和是72，求
这四个数。
解：设四个数中最小的数为x,
根据题意，得方程：
解方程，得：x = 14
答：这四个数分别为14，15，21，22。
日历中同一竖列相邻三个数的和为63，则这三个数分别为_____________；
练习
14、21、28.
例2、元旦某公园的成人的门票每张8元，儿童门票半价（即每张4元），全天共售出门票3000张，收入15600元。问这天售出儿童门票多少张？
解：设售出儿童门票x张
根据题意，得：
解方程，得： x = 2100
答：共售出儿童票2100张
例3、某公司存入银行甲、乙两种不同性质的存款共20万元。甲种存款的年利率为1.4%，乙种存款的年利率为3.7%，该公司一年共得利息6250元，求甲、乙两种存款各多少元？
解：设甲种存款为x万元。则乙种存款为（20 - x)万元
根据题意得：
解方程得： x = 5
所以 20 – x = 15
答：甲种存款为5万元，乙种存款为15万元
练习1：小新的压岁钱已存进银行1年了，已知银行的年利率为1.4%，这次小新共拿出202.8元，你能知道小新存入的压岁钱是多少吗？
那么小新存入1年后可拿出(x+1.4%x)元，
解：设小新存入压岁钱为x元
x+1.4%x = 202.8
解得，x = 200
析：本息和=本金+利息
答：小新存入压岁钱为200元。
练习2：小山上大学向某商人贷款1万元，月利率为6‰ ，1年后需还给商人多少钱？-----------------（ ） A 17200元， B 16000元，
C 10720元， D 10600元
C
例4、某部队开展支农活动，甲队27人，乙队19人，现另调26人去支援，使甲队是乙队的2倍，问应调往甲队、乙队各多少人？
解：设调往甲队x人，则调往乙队（26-x)人
根据题意，得方程：
解方程得：x = 21
答：调往甲队21人。调往乙队5人。
调配问题
例5、已知今年小新与妈妈的年龄和是55岁，妈妈的年龄比小新的年龄的3倍小5岁，那么小新今年多少岁？
析：妈妈的年龄+小新的年龄=55岁
妈妈的年龄=小新的年龄×3 - 5
解：设妈妈的年龄为x岁，那么小新的 年龄为（55- x）岁，根据题意得，
X= 3（55- x）- 5
解得 x=40
答：小新得买40根蜡烛才刚刚好。
例6、商场正在搞活动，为了吸引消费者，商场将进价为80元的毛衣按标价8折销售，仍可获20元的利润，你能说出毛衣的标价吗？
分析：售价-进价=利润
标价× 打折数=售价
解：设毛衣的标价为x元，根据题意得，
80%x=80+20
解得，x=125
答：毛衣的标价为125元。
练习
1、一件衬衫进货价60元,提高50%后标价,则标 价为 _____, 八折优惠价为______,利润
为______；
90元
72元
12元
2、某商品的进价为250元，按标价的9折销售时，利润率为15.2%，商品的标价是多少？
3、某商品的进价为200元，标价为300元，折价销售时的利润率为5%，此商品按几折销售的？
2）商品出售的利润是增长百分率的一类，
等量关系为；
售价=成本价+利润
售价=成本价×（1+利润率）
注：1）一般在成本不知道具体多少的情况下，设为“1”；
3）要注意“利润”和“利润率”的区别，
利润 = 成本×利润率= 销售价－成本价
4、小明去文具店购买2B铅笔，店主说：“如果多买一些，给你打8折。”小明测算了一下，如果买50支，比按原价购买可以便宜6元，那么每支铅笔的原价是多少？
解:每支铅笔的原价是X元
（1－0.8）×５０ X＝６
解得， X＝０．６
答：每支铅笔的原价是０．６元
例7、 A、B两地相距230千米，甲队从A地出发两小时后，乙队从B地出发与甲相向而行，乙队出发20小时后两队相遇，已知乙的速度比甲的速度每小时快1千米，求甲、乙的速度各是多少？
分析：
甲2小时所走的路程
甲20小时所走的路程
乙20小时所走的路程
C
230KM
B
A
D
相等关系：甲走总路程+乙走路程=230
2x
20x
20(x+1)
设：甲速为x千米/时，则乙速为（x+1）千米/时
2x+20x+20(x+1)=230
速度
时间
小结
1、行程问题中的相等关系是：路程=_____×_____．
2、相遇问题常用的等量关系是：
3、追及问题常用的等量关系是：
行程和=速度和×相遇时间．
行程差=速度差×追及时间．
练一练
1、甲乙两人赛跑，甲的速度是8米/秒，乙的速度是5米/秒，如果甲从起点往后退20米，乙从起点处向前进10米，问甲经过几秒钟追上乙？
2、甲、乙骑自行车同时从相距 65千米的两地相向而行，2小时相遇．甲比乙每小时多骑2.5千米，求乙的时速．
解：设乙的速度为x千米/时，则甲的速度为（x+2.5）千米/时，根据题意，得
2(x+2.5)+2x=65
解得：X=15
答：乙的时速为15千米/时．
3、甲、乙两站间的路程为365KM．一列慢车从甲站开往乙站，每小时行驶65KM；慢车行驶了1小时后，另有一列快车从乙站开往甲站，每小时行驶85KM．快车行驶了几小时与慢车相遇？（只列方程不解）
解：快车行驶了x小时后与慢车相遇，根据题意，得
65+x(65+85)=365
4、甲、乙两车自西向东行驶，甲车的速度是每小时48千米，乙车的速度是每小时72千米，甲车开出25分钟后乙车开出，问几小时后乙车追上甲车？
分析：
A
甲先走25分钟的路程
甲走 小时所走的路程
乙走 小时所走的路程
C
B
设x小时后乙车追上甲车
相等关系：
甲走的路程=乙走的路程
X
X
×48
48x
72x
×48+ 48x = 72x
5、甲、乙两位同学练习赛跑，甲每秒跑7米，乙每秒跑6.5米．
（1）如果甲让乙先跑5米，几秒钟后甲可以追上乙？
（2）如果甲让乙先跑1秒，几秒钟后甲可以追上乙？
解：（1）设x秒后甲可以追上乙，根据题意，得
(2)设x秒后甲可以追上乙，根据题意，得
7x-6.5x=5
7x-6.5x=6.5
1、 小明在公路上行走，速度每分钟33米，一辆长为30米的汽车从他的背后驶来，经过他身旁驶过的时间是3秒，则汽车的速度为每小时多少千米 ？
思考题
2、某同学为自己的课堂打了如下的分数：
（1）你得分的二分之一来自于你的实力;
（2）你得分的三分之一来自于你的自信;
（3）你得分的十二分之一来自于同学的合作;
（4）再加8分来自于你我的缘分.
你能知道这位同学的表现到底得了几分吗？
解：设这位同学得了 x 分，由题意得：
解得: x=96
答:这位同学得了96分.
部分量之和=总量
小明编了一道这样的题：我是4月出生的，我的年龄的2倍加上8，正好是我出生那一月的总天数。你猜我有几岁？请你求出小明的年龄。
3、能算出小明的年龄吗？
工程问题中的数量关系：
1） 工作效率=
工作总量
完成工作总量的时间
———————————
2）工作总量=工作效率×工作时间
3）工作时间=
工作总量
—————
工作效率
4）各队合作工作效率=各队工作效率之和
5）全部工作量之和=各队工作量之和
全部工作量“940个”
前3天甲生产零件的个数
后5天甲生产零件的个数
后5 天乙生产零件的个数
后5天生产零件的个数
例题讲解
小结：工程问题常用图示法来表示它的等量关系。
例1、甲每天生产某种零件80个，甲生产3天后，乙也加入生产同一种零件，再经过5天，两人共生产这种零件940个.问乙每天生产这种零件多少个？
例2、王老师带领团员若干人到赤壁游览，现联系了两辆车的车主。甲车主给出的优惠条件是：学生9折，老师不收费；乙车主给出的优惠条件是：包括老师在内，全部按8折优惠。如果每张车票的价格是40元，那么乘哪家车主的车比较合算
质量分数应用题
1、有关质量分数的数量关系：
溶液 = 溶质 + 溶剂
稀释：加水，溶质不变，溶液增加
加浓：加溶质，水不变，溶液增加
蒸发水，溶质不变，溶液减少
100%
×
溶
质
质量分数
＝
溶
液
例 (稀释)：现有含盐16%的盐水30斤，要配制成含盐10%
的盐水,需加水多少斤？
(浓缩) 现有含盐16%的盐水30斤,要配制成含盐20%的
盐水,需蒸发掉水多少斤
(加浓) 现有含盐16%的盐水30斤，要配制成含盐20%
的盐水 ，需加盐多少斤？
能见到你们实在太好了，这几天有一个问题一直困扰着我，可以向你们请教吗？
1、某校七年（10）班学生想邮购2008年北京奥运会吉祥物福娃的毛绒玩具,已知10寸福娃毛绒玩具单价为78元。奥运特许商店规定两种邮购付费方式：A.邮购20个玩具以内(包括20个),另需收15元邮购费。若超过20个，超过20个的部分每个加收邮购费6元。B.每个玩具都收单价的5%邮购费。
（１）请问邮购40个这种毛绒玩具，A、B两种方式各需多少钱？
（２）求邮购多少个毛绒玩具时(假设多于20个)，上述两种方式付费相同。
综合应用
2、今年5月27日，印尼中爪哇省发生强烈地震，给当地人民造成巨大的经济损失。某学校积极组织捐款支援灾区，初三（1）班55名同学共捐款274元，捐款情况如下表。表中捐2元和5元的人数不小心被墨水污染已看不清楚，请你帮助确定表中数据，并说明理由。
解:设捐2元的同学有X人
则捐5元的同学有(55-6-7-X)人
1 ×6 ＋ 2X ＋ 5×(42-X)＋10 ×7 =274
解得,X=4
则捐5元的同学有: 42-X=42-4=38
答:捐2元的同学有4人,捐5元的同学有38人
3、数学庄园的牛奶加工厂已经开工喽！现有鲜奶9吨。这几天，经过市场调查发现：在市场上直接销售鲜奶，每吨可获得利润500元；制成酸奶销售，每吨可获得利润1200元；制成奶片销售，每吨可获得利润2000元。
工厂生产能力是：如制成酸奶，每天可加工3吨；制成奶片，每天可加工1吨。
受人员限制，两种加工方式不可同时进
行，那么请问怎样安排才能使这批牛奶在
4天内(包括4天）全部销售或加工完？
各方案的最终利润情况又如何呢？
4、如图,在宽为20m,长为X m的长方形地面上修筑同样宽为2 m的道路(图中空白部分),余下的部分种上草坪，要使草坪的面积为540m2，求长方形的长为多少
方法一、解:设长方形的长为X米
20X－2X－2×20＋2 × 2＝540
解得，X=32
答：长方形的长为32米
方法二、解:设长方形的长为X米
解得，X=32
答：长方形的长为32米
4、如图,在宽为20m,长为X m的长方形地面上修筑同样宽为2 m的道路(图中空白部分),余下的部分种上草坪，要使草坪的面积为540m2，求长方形的长为多少
（20 － 2）（ X－2） ＝540
4、如图,在宽为20m的长方形地面上修筑同样宽为2m的道路(图中白色部分),余下的部分种上草坪，要使草坪的面积为540m2，求长方形的长为多少
方法一、解:设长方形的长为X米
20X－2X－2×20＋2 × 2＝540
解得，X=32
答：长方形的长为32米
4、如图,在宽为20m的长方形地面上修筑同样宽为2m的道路(图中白色部分),余下的部分种上草坪，要使草坪的面积为540m2，求长方形的长为多少
方法二、解:设长方形的长为X米
解得，X=32
答：长方形的长为32米
（20－2）（X－2）＝540
5、 将一箱苹果分给若干个小朋友，若每个小朋友分5个苹果，则还剩12个；若每个小朋友分8个苹果，则有一个小朋友分不到8个。求这一箱苹果的个数与小朋友的人数.
课外拓展
1、一名落水儿童抱着木头在河中漂流，在某处遇到逆水而上的轮船，因雾太大，轮船上人未发现小孩。1小时后该轮船上的人获悉此事，随即掉头追赶，则从获悉此事到追上小孩需多少小时？
课外拓展
2、一个三位数三个数字之和是24，十位数字比百位数字少2，如果这个三位数减去两个数字都与百位数字相同的一个两位数所得的数也是三位数，而这三位数三个数字的顺序和原来三位数的顺序恰好颠倒。求原来的三位数。
设百位数字为x，则
[100x+10（x－2）+（26-2x）]－（10x+x）
=100（26－2x）+10（x－2）+x
练：一个三位数，它的百位上的数比十位上的数的2倍 大1，个位上的数比十位上的数的3倍小1，如果把这个三位数的百位上的数字和个位上的数字对调，那么得到的三位数比原来的三位数大99，求原来的三位数。
3、甲、乙两班学生到集市上购买苹果，苹果的价格如下：
甲班分两次共购买70千克（第二次多于第一次），共付出189元，乙班则一次购买苹果70千克。
（1）乙班比甲班少付出多少元？
（2）甲班第一次、第二次分别购买苹果多少千克？
购买苹果数 不超过30千克 30以上但不超过50千克 50千克以上
每千克价格 3元 2.5元 2元
谢谢，你们用数学知识帮我解决了难题，太感谢啦！
一列火车长300米,某人如果和火车同向而行,经过18秒整列火车从该人身旁驶过;如果该人和火车相向而行,则经过15秒整列火车从该人身旁驶过,分别求该人和火车的速度.
一列火车长300米,某人如果和火车同向而行,经过18秒整列火车从该人身旁驶过;如果该人和火车相向而行,则经过15秒整列火车从该人身旁驶过,分别求该人和火车的速度.
火车18秒行的路程
人18秒行的路程
火车的车身长
火车15秒行的路程
人15秒行的路程
火车的车身长
祝同学们学数学
越学越好！