一次函数复习课学案稿

本资料来自于资源最齐全的２１世纪教育网www.21cnjy.com
一次函数的应用复习课学案稿
【课前练习】
1.已知，直线与平行，且过点（1，-2），则直线不经过( ) A.第一象限 B.第二象限 C. 第三象限 D. 第四象限
2．图1是水滴进玻璃容器的示意图（滴水速度不变），图2是容器中水高度随滴水时间变化的图像.
给出下列对应：（1）：（a）——（e） （2）：（b）——（f） （3）：（c）——h （4）：（d）——（g）其中正确的是( )
（A）（1）和（2） （B）（2）和（3） （C）（1）和（3） （D）（3）和（4）
3、据报载，某地区人均耕地面积己从1951年的2.94亩减少到1999年的1.02亩，平均每年减少0.04亩，若不采取措施，继续按这样的速度减少下，若干年后该地区将无地可种，这种情况最早会发生在（ ）
　 A　2025年　　B　2024年　　　C　2023年　　D　2022年
【例题解析】
1．小张骑车往返于甲、乙两地，距甲地的路程(千米)与时间(小时)的函数图象如图所示．
（1）小张在路上停留__________小时，他从乙地返回时骑车的速度为__________千米/时．
（2）小李与小张同时从甲地出发，按相同路线匀速前往乙地，到乙地停止．途中小李与小张共相遇3次．请在图中画出小李距甲地的路程(千米)与时间(小时)的函数的大致图象．
（3）小王与小张同时出发，按相同的路线前往乙地，距甲地的路程(千米)与时间(小时)的函数关系为．小王与小张在途中共相遇几次？请你计算第一次相遇的时间．
2.某机动车出发前油箱内有油42升，行驶若干小时后，途中在加油站加油若干升。油箱中剩余油量Q（升）与行驶时间t（时）的函数关系如图所示，根据图象回答问题：
①机动车行驶几小时后加油？
②机动车每小时耗油多少升？
③中途加油多少升？
④如果加油站距目的地还有230公里，机动车平均每小时行驶40公里，要到达目的地，油箱中的油是否够用？
3．已知雅美服装厂现有A种布料70米，B种布料52米，现计划用这两种布料生产M、N两种型号的时装共80套．已知做一套M型号的时装需用A种布料1.1米，B种布料0.4米，可获利50元；做一套N型号的时装需用A种布料0.6米，B种布料0.9米，可获利45元．设生产M型号的时装套数为x，用这批布料生产两种型号的时装所获得的总利润为y元．
①求y（元）与x（套）的函数关系式，并求出自变量的取值范围；
②当M型号的时装为多少套时，能使该厂所获利润最大？最大利润是多？
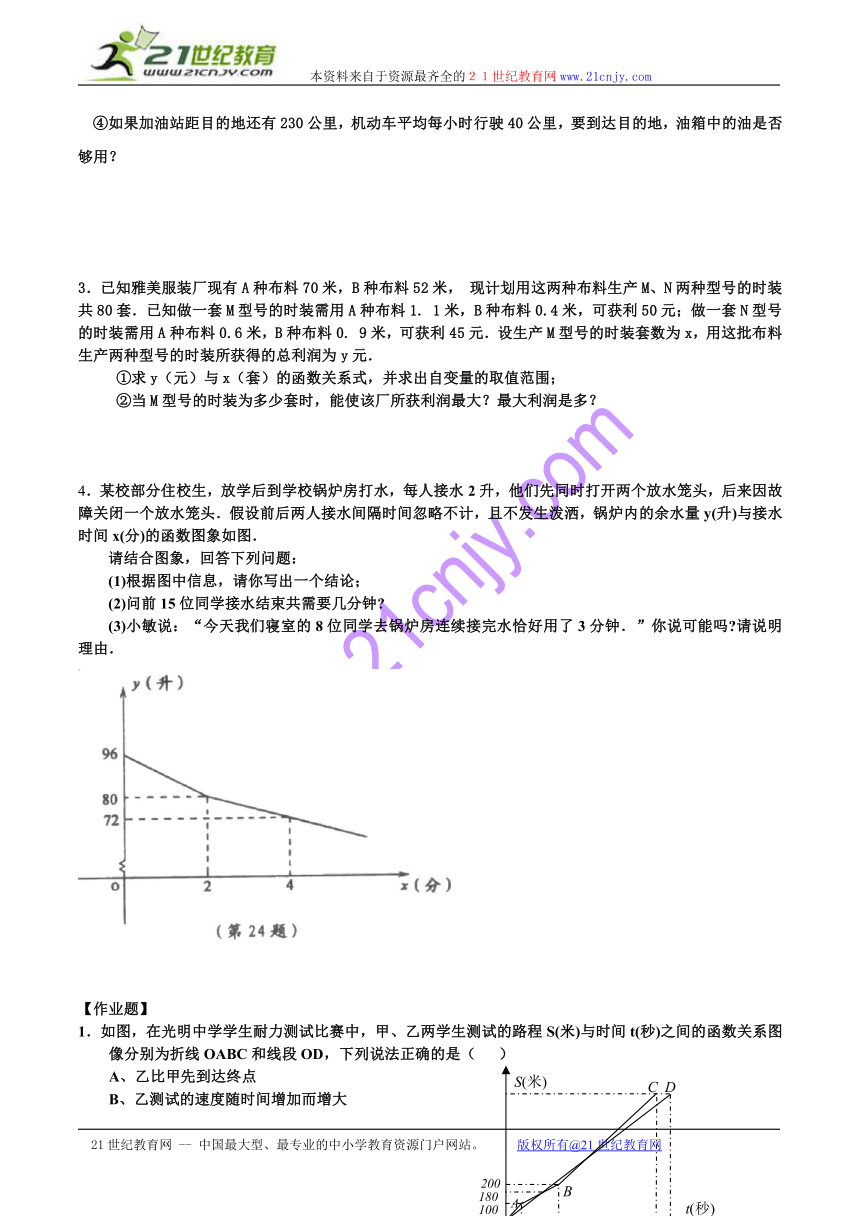
4．某校部分住校生，放学后到学校锅炉房打水，每人接水2升，他们先同时打开两个放水笼头，后来因故障关闭一个放水笼头．假设前后两人接水间隔时间忽略不计，且不发生泼洒，锅炉内的余水量y(升)与接水时间x(分)的函数图象如图．
请结合图象，回答下列问题：
(1)根据图中信息，请你写出一个结论；
(2)问前15位同学接水结束共需要几分钟
(3)小敏说：“今天我们寝室的8位同学去锅炉房连续接完水恰好用了3分钟．”你说可能吗 请说明理由．
( http: / / www.21cnjy.com / )
【作业题】
1．如图，在光明中学学生耐力测试比赛中，甲、乙两学生测试的路程S(米)与时间t(秒)之间的函数关系图像分别为折线OABC和线段OD，下列说法正确的是（ ）
A、乙比甲先到达终点
B、乙测试的速度随时间增加而增大
C、比赛进行到29.4秒时，两人出发后第一次相遇
D、比赛全程甲的测试速度始终比乙的测试速度快
2. 根据下图所示的程序计算函数值，若输入的x值为，则输出的结果为
3.不论k为何值，一次函数y=kx-2k+1的图象经过一定点，则这个定点是_______．
4．已知y-4与x成正比例，且当x=6时，y=-4.
（1）求y与x的函数关系式；
（2）设点P在y轴的负半轴上，（1）中函数的图像与x轴、y轴分别交于A、B2点，且以A、B、P为顶点的三角形面积为9，试求点P的坐标．
5.有两段长度相等的河渠挖掘任务，分别交给甲、乙两个工程队同时进行挖掘．图11是反映所挖河渠长度y（米）与挖掘时间x（时）之间关系的部分图象．请解答下列问题：
（1）乙队开挖到30米时，用了_____小时．开挖6小时时，
甲队比乙队多挖了______米；
（2）请你求出：
①甲队在0≤x≤6的时段内，y与x之间的函数关系式；
②乙队在2≤x≤6的时段内，y与x之间的函数关系式；
③开挖几小时后，甲队所挖掘河渠的长度开始超过乙队？
（3）如果甲队施工速度不变，乙队在开挖6小时后，施工速度增加到12米/时，结果两队同时完成了任务．问甲队从开挖到完工所挖河渠的长度为多少
6． 依法纳税是每个公民应尽的义务．《中华人民共和国个人所得税法》规定，公民每月收入不超过1600元，不需交税；超过1600元的部分为全月应纳税所得额，都应纳税，且根据超过部分的多少按不同的税率纳税，详细的税率如下表：
级别 全月应纳税所得额 税率
1 不超过500元的 5
2 超过500元至2 000元的部分 10
3 超过2 000元至5 000元的部分 15
… … …
（1）某工厂一名工人2006年5月的收入为2 000元，问他应交税款多少元？
（2）设表示公民每月收入（单位：元），表示应交税款（单位：元），当时，请写出关于的函数关系式；
（3）某公司一名职员2006年5月应交税款120元，问该月他的收入是多少元？
7．A市、B市和C市分别有某种机器10台、10台和8台，现在决定把这些机器支援给D市18台、E市10台，已知：从A市调运一台机器到D市、E市的运费分别为200元和800元；从B市调运一台机器到D市、E市的运费分别为300元和700元；从C市调运一台机器到D市、E市运费分别为400元和500元．
(1)设从A市、B市各调x台到D市，当28台机器全部调运完毕后，求总运费W（元）关于x（台）的函数式，并求W的最小值和最大值．
(2)设从A市x台到D市，B市调y台到D市，当28台机器全部调运完毕后，用x，y表示总运费W（元），并求W的最小值和最大值．
t(秒)
S(米)
C
D
B
A
O
145
147
33
15
100
180
200
第1题
输入x值值
输出Y值值
6
2
O
x(时)
y(米)
30
60
乙
甲
50
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网