5.5平行四边形的判定(1)

课件18张PPT。5.5 平行四边形的判定（1）AD= ，AB= ， ∠ABC=∠ ， ∠DAB=∠ ，AO= ，BO= ， AD∥ ，AB∥ ， ∠1=∠ ，∠3=∠ ， △AOB≌△ ，△AOD≌△ ，△ABC≌△ ，△ABD≌△ 。
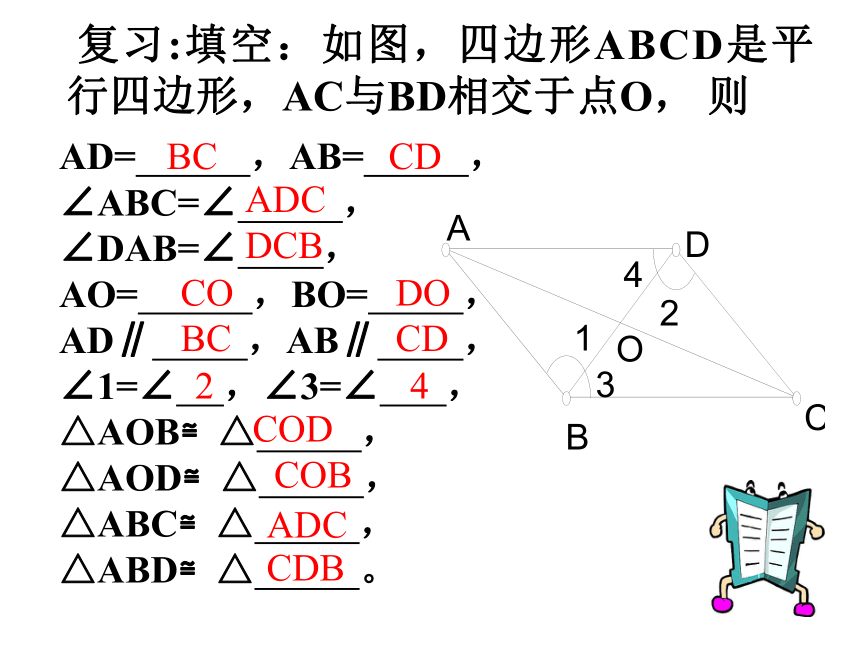
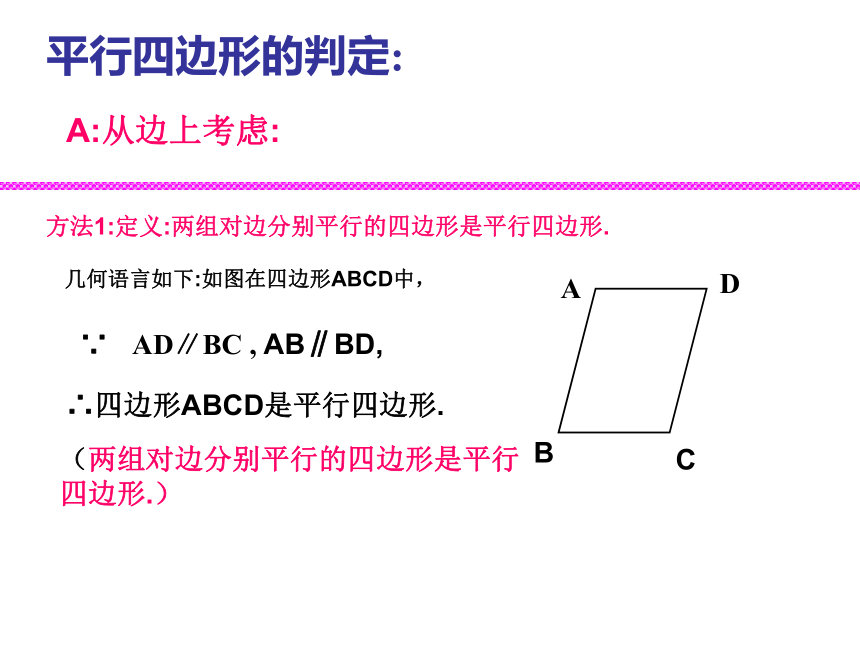
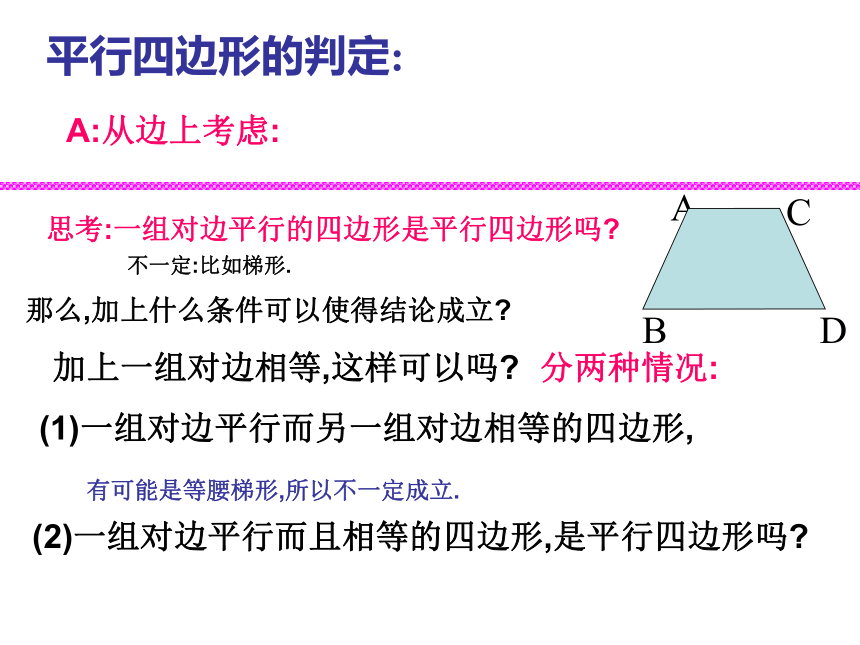
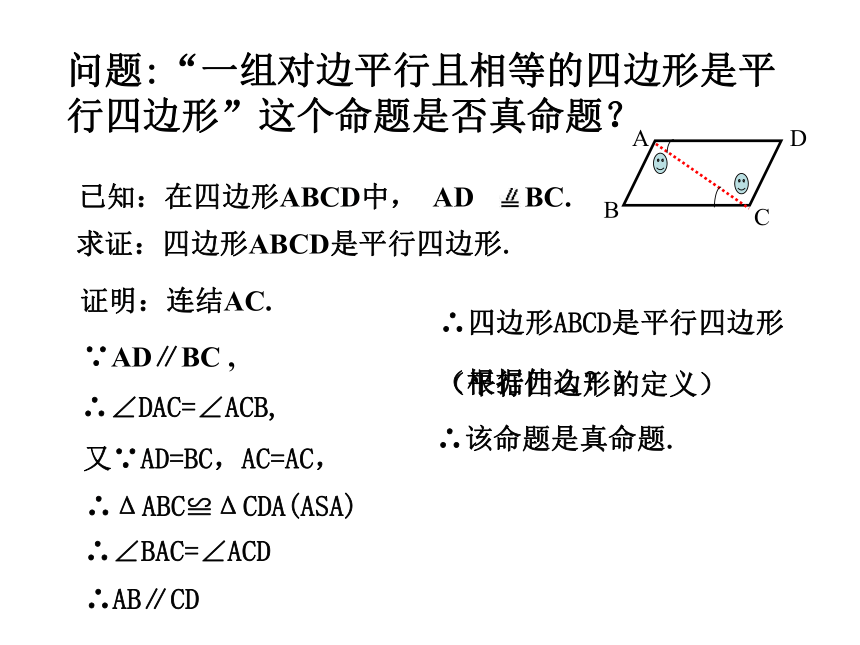
复习:填空：如图，四边形ABCD是平行四边形，AC与BD相交于点O， 则BCCDADCDCBCODOBCCD24CODCOBADCCDB∵ AD∥BC , AB∥BD, 平行四边形的判定:方法1:定义:两组对边分别平行的四边形是平行四边形.∴四边形ABCD是平行四边形.A:从边上考虑: 几何语言如下:如图在四边形ABCD中，（两组对边分别平行的四边形是平行四边形.）不一定:比如梯形.平行四边形的判定:思考:一组对边平行的四边形是平行四边形吗?那么,加上什么条件可以使得结论成立?A:从边上考虑:(1)一组对边平行而另一组对边相等的四边形,加上一组对边相等,这样可以吗?分两种情况:有可能是等腰梯形,所以不一定成立.(2)一组对边平行而且相等的四边形,是平行四边形吗?问题:“一组对边平行且相等的四边形是平行四边形”这个命题是否真命题？ 求证：四边形ABCD是平行四边形. 证明：连结AC. ∵AD∥BC ,∴∠DAC=∠ACB,又∵AD=BC，AC=AC， ∴ΔABC≌ΔCDA(ASA)∴∠BAC=∠ACD∴AB∥CD ∴该命题是真命题. （根据什么？） ∴四边形ABCD是平行四边形 （平行四边形的定义）已知：在四边形ABCD中， AD 　BC.其几何语言为:方法2:判定定理1 :
一组对边平行并且相等的四边形是平行四边形。 在四边形ABCD中， ∴四边形ABCD是平行四边形.
(一组对边平行并且相等的四边形是平行四边形)∵ AD 　BC.
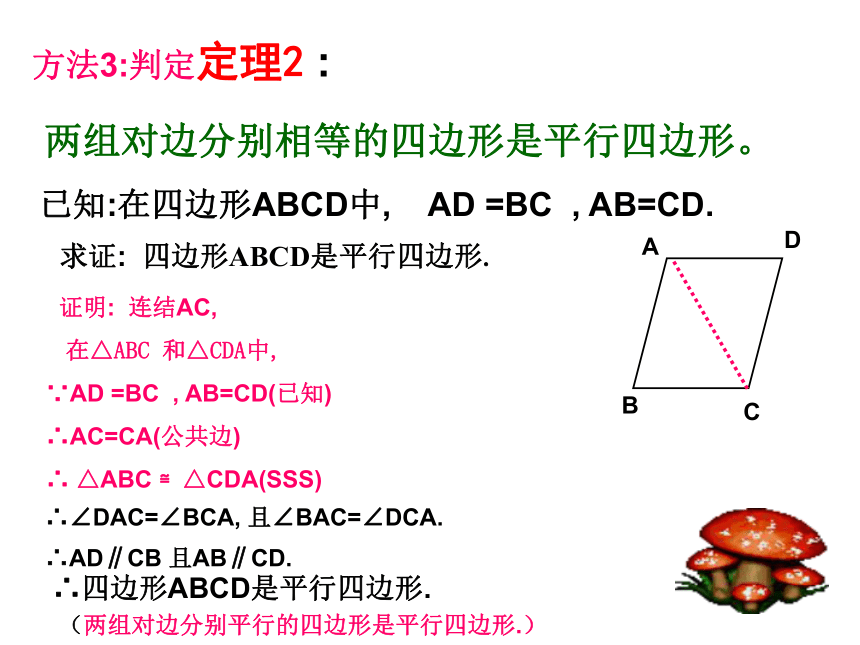
方法3:判定定理2 :
两组对边分别相等的四边形是平行四边形。求证: 四边形ABCD是平行四边形. 已知:在四边形ABCD中, AD =BC , AB=CD. 证明: 连结AC,
在△ABC 和△CDA中,
∵AD =BC , AB=CD(已知)
∴AC=CA(公共边)
∴ △ABC ≌△CDA(SSS) ∴∠DAC=∠BCA, 且∠BAC=∠DCA. ∴AD∥CB 且AB∥CD. ∴四边形ABCD是平行四边形.（两组对边分别平行的四边形是平行四边形.）其几何语言为:方法3:判定定理2 :
两组对边分别相等的四边形是平行四边形。 在四边形ABCD中， ∴四边形ABCD是平行四边形.
(两组对边分别相等的四边形是平行四边形)∵ AD =BC , AB=CD. 一般的，我们有下面判定一个四边形是平行四边形的定理：定理1: 一组对边平行并且相等的四边形 是平行四边形。定理2: 两组对边分别相等的四边形是平行四边形。 例1 已知：如图，平行四边形ABCD中，E，F分别是边AB，CD的中点，求证:EF=BC. ∵ 四边形ABCD是平行四边形， 证明： ∵ E，F分别是边AB，CD的中点 .∴ 四边形EBCF是平行四边形. （一组对边平行且相等的四边形是平行四边形） ∴ EF=BC（平行四边形对边相等） 1.已知：如图，E,F分别是 的边AD,BC的中点。
求证：BE=DF.D证明：∵四边形ABCD是平行四边形，∴AB∥CD (平行四边形的定义)AD=BC(平行四边形的对边分别相等)，∵E,F分别是AD,BC的中点，∴四边形EBFD是平行四边形（一组对边 平行并且相等的四边形是平行四边形）。课内练习∴BE=DF(平行四边形的对边分别相等)。2。已知：如图，CD是线段AB经平移所得的像，连结AD,BC.
求证：四边形ABCD是平行四边形。DCBA证明：∵CD是AB经平移所得的像，∴四边形ABCD是平行四边形.（一组对边平行并且相等的四边形是平行四边形）。课内练习3.已知：如图，AD⊥AC,BD⊥AC,且AB=CD.
求证：AB∥CD.DCAB证明：∵AD⊥AC, BC⊥AC,∴AD∥BC, ∠BCA=∠DAC=90O,又∵AB=CD, AC=CA,∴Rt⊿ACB≌Rt⊿CAD.课内练习巩固练习已知：如图 ,在□ABCD中，E，F分别是边AD，BC的中点．求证：EB=DF． FEDCABGH（1）连接AF、EC分别交BE、DF于点G、点H，
你能得出什么结论？ 小组同学讨论。拓展练习（2）连接GH，你又能 得出什么结论？思考:B.从角上考虑,如何判定平行四边形?两组对角分别相等的四边形是平行四边形.方法4:推论1已知：如图，四边形ABCD中, ∠A=∠C, ∠B=∠D.
求证：四边形ABCD是平行四边形。证明: 在四边形ABCD中,
∵ ∠A=∠C, ∠B=∠D.
∴ ∠A+ ∠B=∠C+∠D.
∵∠A+ ∠B+∠C+∠D=360°.
∴ ∠A+ ∠B=∠C+∠D=180°,
∴ AD∥BC,
同理可得 AB∥CD,
∴四边形ABCD是平行四边形。
(两组对边分别平行的四边形是平行四边形) 思考:C.从边和角上共同考虑,如何判定平行四边形? 有一组对边平行,一组对角相等的四边形是平行四边形.方法5:推论2已知：如图，四边形ABCD中, ∠A=∠C, AD∥CB.
求证：四边形ABCD是平行四边形。证明: ∵ AD∥CB,
∴ ∠A+ ∠B=180°.
∴ ∠A=∠C,
∴∠C+∠B=180°,
∴ AB∥DC,
∴四边形ABCD是平行四边形.
(两组对边分别平行的四边形是平行四边形) 还可以从哪个方向考虑呢?小结：
这节课你学会了什么？知道了什么？作业布置：
作业本