第五章 平行四边形复习

课件32张PPT。第5章 平行四边形复习本章要点聚焦一、四边形的概念
1.定义：在同一平面内，由不在同一直线上的四条线段首尾顺次相接组成的图形.
2.四边形的内角和与外角和均为360°.
3.四边形具有不稳定性.
4.多边形内角和定理：n边形的内角和等于(n-2)·180°
5.多边形外角和定理：n边形的外角和等于360°.
6.多边形的对角线.二.重要知识规律总结:n边形共有对角线 条(n≥3)1.多边形的对角线. n边形从一个顶点出发的对角线有(n－3)条(n≥3).n边形的内角和为：（n－2)×180°(n≥3).2.多边形的内角和公式.3.平行四边形的性质有：平行四边形的对边相等平行四边形的对边平行平行四边形的对角相等平行四边形的对角线互相平分平行四边形邻角互补平行四边形是中心对称图形☆两个推论:夹在两条平行线间的平行线段相等夹在两条平行线间的垂线段相等定理2：两组对边分别相等的四边形是平行四边形.定义: 两组对边分别平行的四边形是平行四边形.定理1: 一组对边平行且相等的四边形是平行四边形. 4.平行四边形的判定:定理3：对角线互相平分的四边形是平行四边形．定理4：两组对角分别相等的四边形是平行四边形.推论1:有一组对边平行且有一组对角相等的四边形是平行四边形 .　 三角形的中位线平行于第三边，并且等于第三边的一半.5.三角形的中位线6.逆命题与逆定理.重要逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形定理1:到一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.定理2:如果三角形一边上的中线等于这边一半,那么这个三角形是直角三角形定理3:7、中心对称一个图形绕一点旋转180度后与原来图形重合.中心对称图形: 关于一点成中心对称:一个图形绕一点旋转180度后与另一图形互相重合.性质:对称中心平分连接两个对称点的线段直角坐标系中, 点(x,y)关于原点对称的点是(-x,-y)3、如图，在锐角△ABC中，CD、BE分
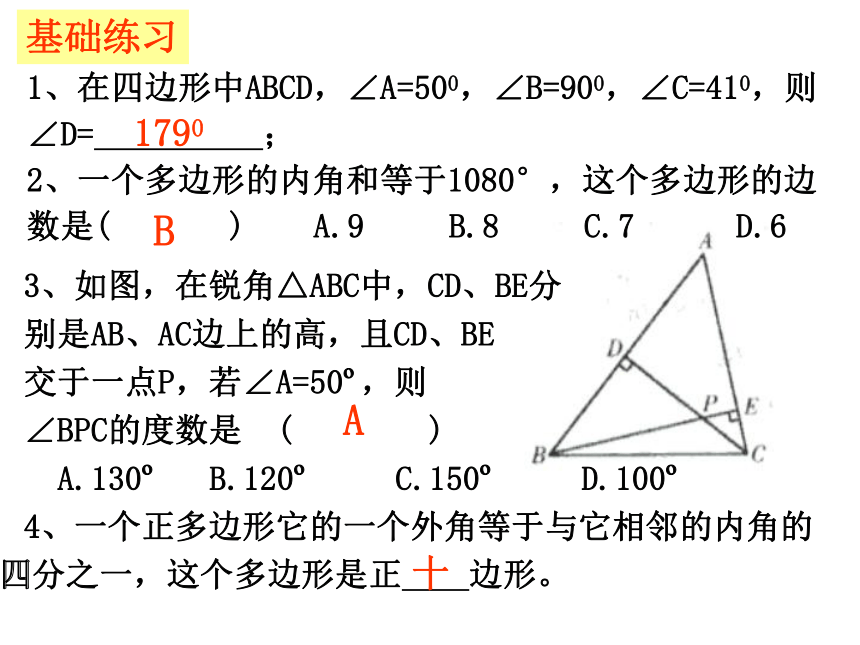
别是AB、AC边上的高，且CD、BE
交于一点P，若∠A=50o，则
∠BPC的度数是 ( )
A.130o B.120o C.150o D.100o
4、一个正多边形它的一个外角等于与它相邻的内角的　　四分之一，这个多边形是正　　边形。B1、在四边形中ABCD，∠A=500，∠B=900，∠C=410，则∠D= ；
2、一个多边形的内角和等于1080°，这个多边形的边数是( ) A.9 B.8 C.7 D.6A十1790基础练习5、下例不能判定四边形ABCD是平行四边形的是（ ）
A、AB=CD AD=BC B、AB=CD AB∥CD
C、AB=CD AD∥BC D、AB ∥CD AD∥BC
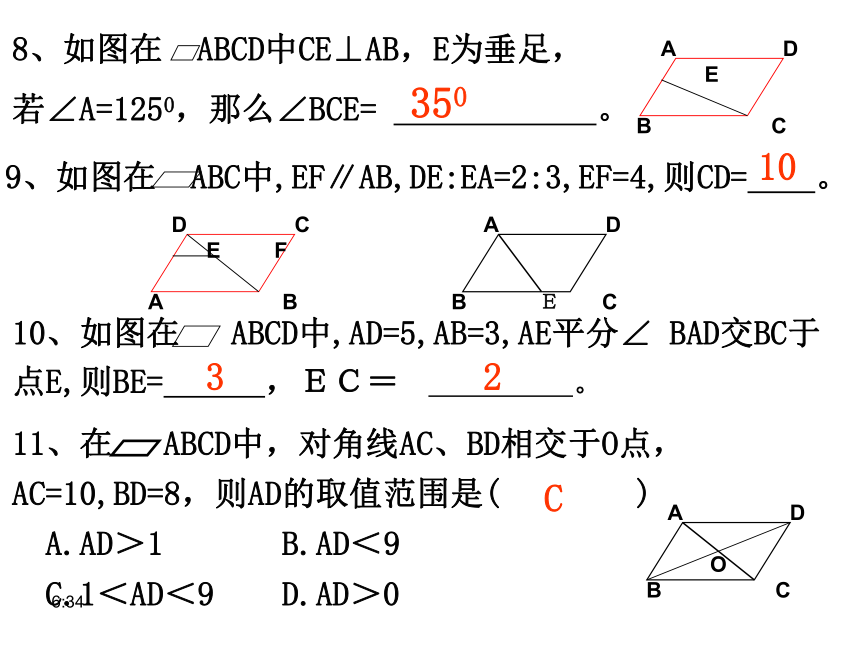
6、如图所示，在△ABC中，D、E、F分别为AB、BC、CA边的中点，则图中共有平行四边形( )
A.1个 B.2个 C.3个 D.4个CCBE=DF、BF=DE，AE∥FC、AF∥EC3501032C12、判断题:
（1）邻角互补的四边形是平行四边形.
（2）一组对边平行,另一组对边相等的四边形是平行四边形.
（3）一组对边平行, 一组对角相等的四边形是平行四边形.
（4）对角线相等的四边形是平行四边形.13、某人到瓷砖商店去购买一种多边形形状的瓷砖，用来铺设无缝地板．他购买的瓷砖形状不可以是（ ）
（A）正三角形 （B）正四边形
（C）正八边形 （D）正六边形 14、平行四边形一边长为12cm，那么它的两条对角线的长度可能是（ ）．
（A）8cm和14cm （B）10cm和14cm
（C）18cm和20cm （D）10cm和34cmCC15、在平行四边形ABCD中,AC=10,BD=8,则AB的取值范围是( )
A、2 C、AB>2 D、AB<916、平行四边形一边长为 10 ,则它的两条对角线可以是( )
A、6 ,8 B、8, 12
C、8, 14 D、6, 14BC例题解析【例2】 如图所示，已知? ABCD的周长为30cm，AE⊥BC于E点，AF⊥CD于F点，且AE∶AF=2∶3，∠C=120°，求S ABCD. 27 (cm2).
C（2√3，-2 ）C（-2√3，2 ）
【例3】如图Rt△OAB的两条直角边都在坐标轴上，AO=2，∠OBA=300，求以O、A、B为其中三个顶点的平行四边形的第四个顶点C的坐标。 C（2√3，2 ）
A
O B 【例4】如图已知平行四边形ABCD的周长是14，两条对角线AC：BD=2：3，AC与BD交于O，△AOB和△BOC
的周长和是17， 则AC= ，BD= 。【例5】如图在△ABC中点D、E分别是AB，AC边的中点，若把△ADE饶着点E顺时针旋转1800得到△CEF。　　　　　　　　　　　　　　　（1）请指出图中哪些线段与线段CF相等；　　　　　　　　　　　　　　　　（2）试判断四边形DBCF是怎样的四边形？证明你的结论。练一练2、四边形ABCD中，AD//BC，那么∠Ａ：∠Ｂ：∠Ｃ：∠Ｄ的值可能是（ ） 1、在一个四边形中，∠Ａ：∠Ｂ：∠Ｃ：∠Ｄ＝９：５：３：７，求这个四边形各内角的度数？A、９：5：３：７ B、２：３：４：５
C、３：5：２：4 D、２：5：４：３3 、一个多边形,除了一个内角外,其余内角和为1205度,则这个内角是多少度,这是个几边形?D4、如图,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是( )
A.5 B.10 C.15 D.20 B4cm3cmO变式：已知如图四边形ABCD和四边形BFDE都是平行四边形,
求证：AE=CF10、已知:如图,四边形ABCD是平行四边形,△ADE和△BCF都是等边三角形.求证:BD和EF互相平分.ABCFDE11、已知:如图,O是等边三角形ABC内任意一点,OD∥BC,OE∥AC,OF∥AB,点D,E,F分别在AB,BC,AC上.
求证:OD+OE+OF=BC.AFOEDBCMN12、请说出“等腰三角形两腰上的高相等”的逆命题．这个逆命题是真命题吗？请证明你的判断. 1.如图,请作一个平行四边形ABCD.2.已知:线段a、b,∠1.求作一个平行四边形ABCD,使AB=a,BC=b, ∠B= ∠1.作图应用3、如图，在 ?ABCD中，已知两条对角线相交于点O，E、F、G、H分别是AO、BO、CO、DO的中点，以图中的点为顶点，尽可能多地画出平行四边形。ADCBEFGHO我们知道,三角形的三条中线交于一点.这一点 叫做三角形的重心.三角形的重心分每一条中线的比为1∶2(重心到每边的中点距离∶重心到所对角的顶点的距离).你能证明这个命题吗?三角形的重心有一个重要的几何性质:探索提高证明一：连结EF，利用三角形的中位线按理证明已知:如图,AE,BF,CD是△ABC的三条中线,且相交于点G.分析:要证明GE∶GA=1∶2,可以考虑折半法(如取GA的中点M,GB的中点N).转化为证明AM=MG=GE,BN=NG=GF.分别连接FE,EN,NM,MF.求证:GE∶GA=GF∶GB=GD∶GC=1∶2.从而借助于三角形的中位线构造平行四边形来获得证明.证明二：证明:取GA的中点M,GB的中点N,分别连接FE,EN,NM,MF.∵F,E是AC,BC的中点,∴ FE∥MN,FE=MN.∴四边形FENM是平行四边形.∴MG=GE,NG=GF.∴FE∥AB,MN∥AB,∴AM=MG=GE,BN=NG=GF.∴ GE∶GA=GF∶GB=1∶2.同理,GD∶GC=1∶2..∴GE∶GA=GF∶GB=GD∶GC=1∶2.已知:如图,AE,BF,CD是△ABC的三条中线,且相交于点G.求证:GE∶GA=GF∶GB=GD∶GC=1∶2.再见