第五章平行四边形和判断复习课

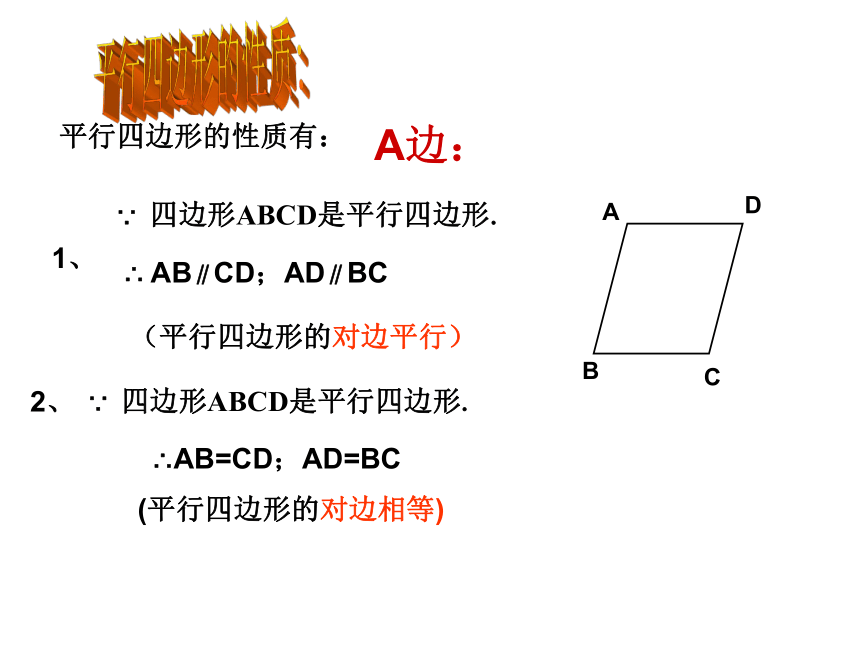
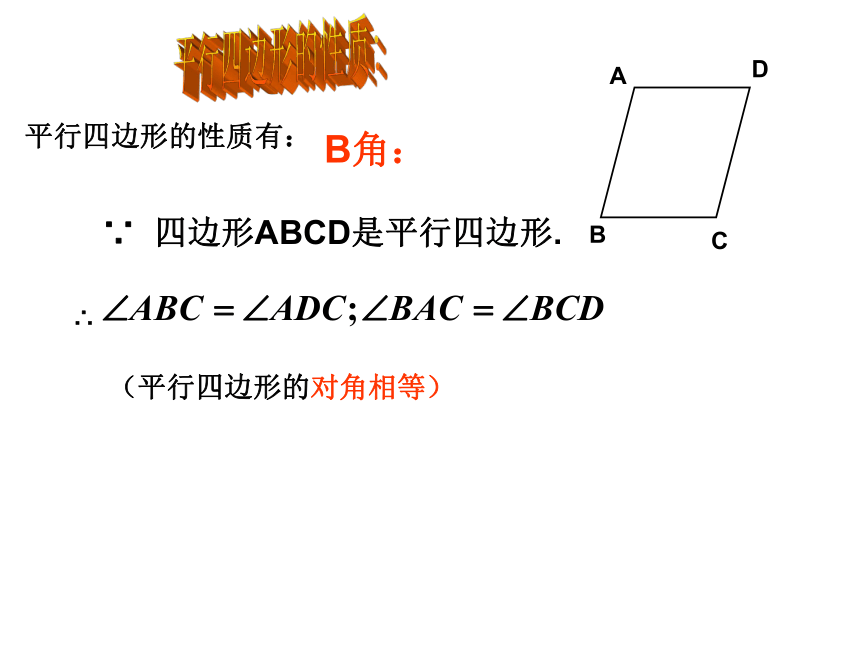
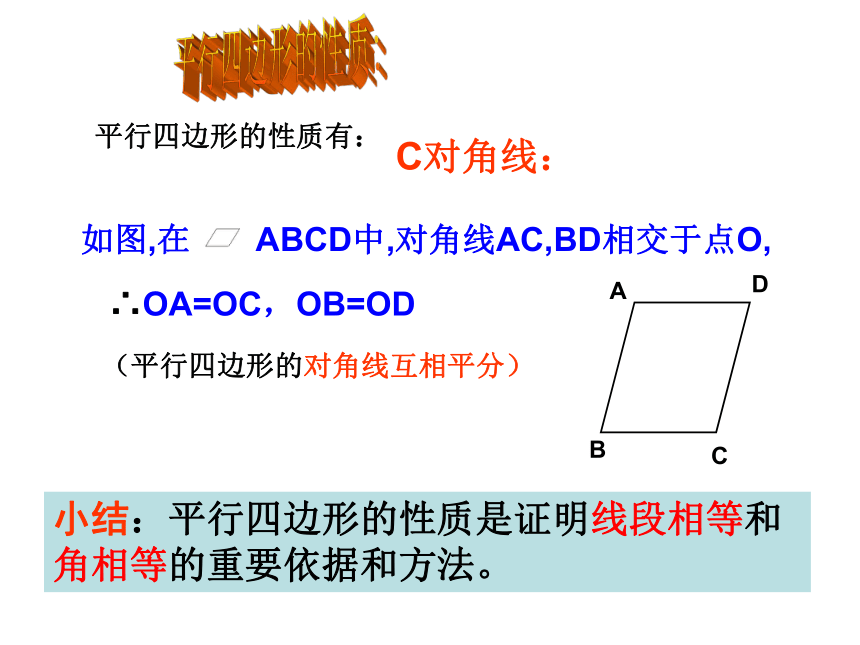
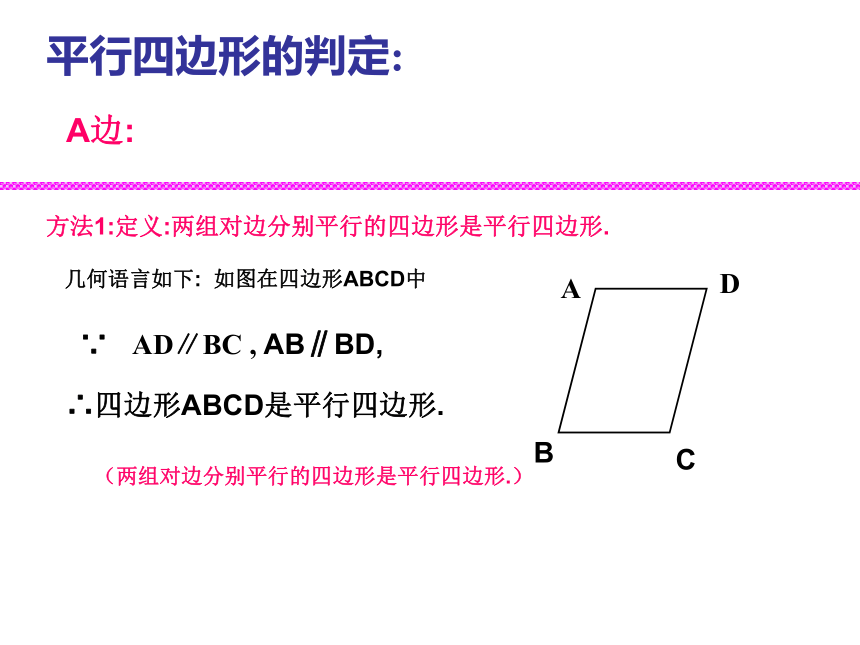
课件29张PPT。平行四边形的性质与判定复习课平行四边形的性质:平行四边形的性质有：(平行四边形的对边相等)（平行四边形的对边平行）∴AB=CD；AD=BC∴ AB∥CD；AD∥BCA边：∵ 四边形ABCD是平行四边形. 1、∵ 四边形ABCD是平行四边形. 2、平行四边形的性质: 平行四边形的性质有：（平行四边形的对角相等）B角：∵ 四边形ABCD是平行四边形. ∴平行四边形的性质:平行四边形的性质有：（平行四边形的对角线互相平分）小结：平行四边形的性质是证明线段相等和角相等的重要依据和方法。C对角线：∴OA=OC，OB=OD∵ AD∥BC , AB∥BD, 平行四边形的判定:方法1:定义:两组对边分别平行的四边形是平行四边形.∴四边形ABCD是平行四边形.A边: 几何语言如下: 如图在四边形ABCD中（两组对边分别平行的四边形是平行四边形.）其几何语言为:方法2:判定定理1 :
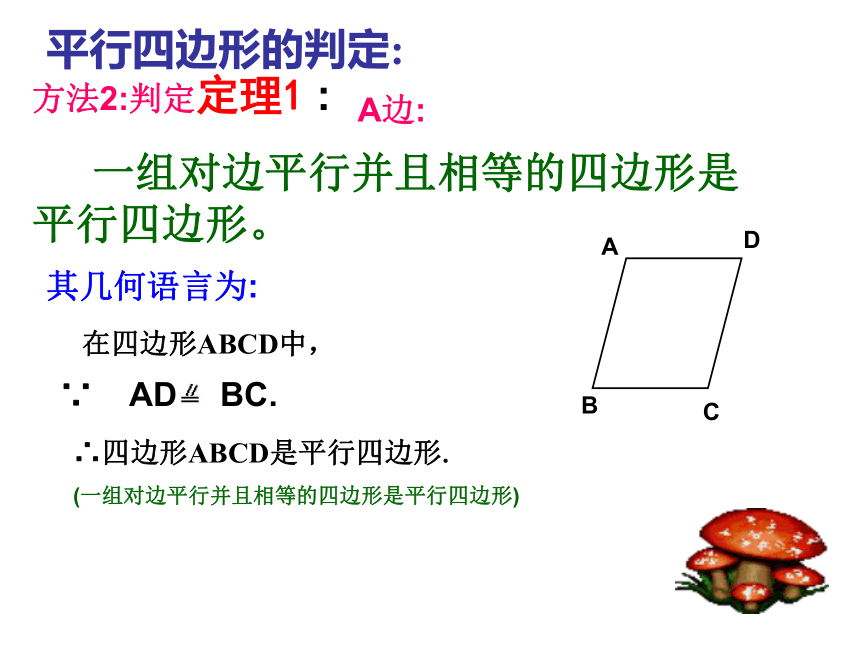
一组对边平行并且相等的四边形是平行四边形。 在四边形ABCD中， ∴四边形ABCD是平行四边形.
(一组对边平行并且相等的四边形是平行四边形)∵ AD 　BC.
A边:平行四边形的判定:其几何语言为:方法3:判定定理2 :
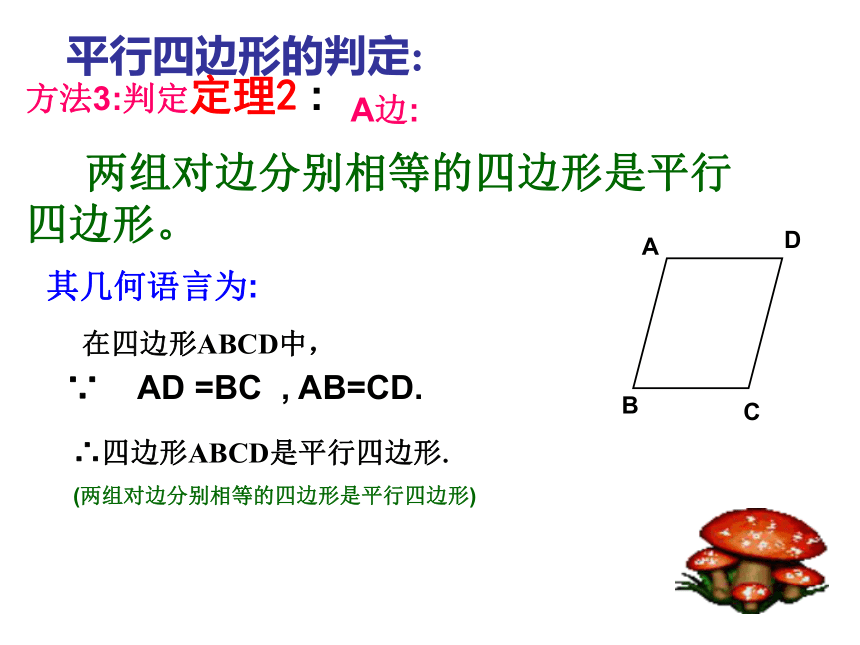
两组对边分别相等的四边形是平行四边形。 在四边形ABCD中， ∴四边形ABCD是平行四边形.
(两组对边分别相等的四边形是平行四边形)∵ AD =BC , AB=CD.
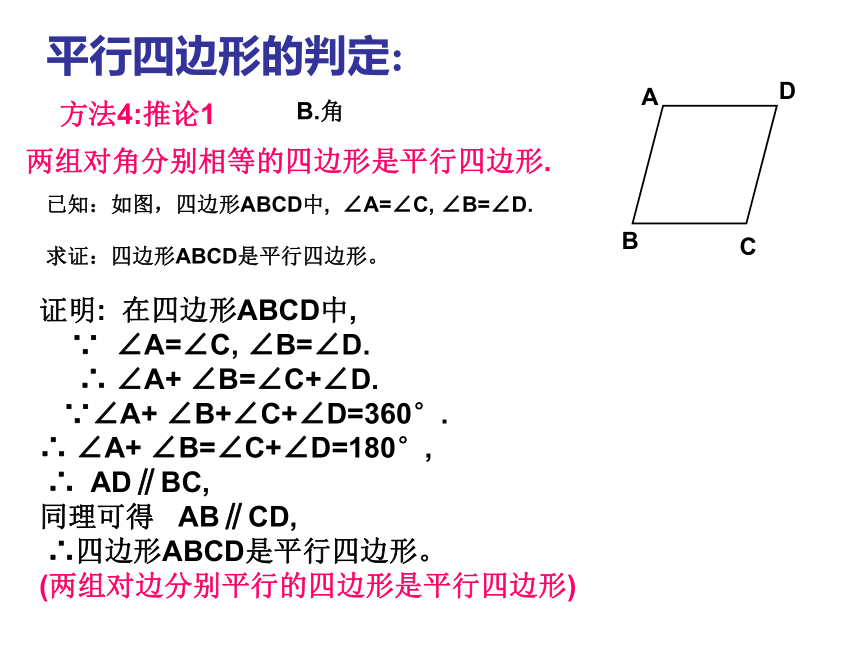
A边:平行四边形的判定:B.角两组对角分别相等的四边形是平行四边形.方法4:推论1已知：如图，四边形ABCD中, ∠A=∠C, ∠B=∠D.
求证：四边形ABCD是平行四边形。证明: 在四边形ABCD中,
∵ ∠A=∠C, ∠B=∠D.
∴ ∠A+ ∠B=∠C+∠D.
∵∠A+ ∠B+∠C+∠D=360°.
∴ ∠A+ ∠B=∠C+∠D=180°,
∴ AD∥BC,
同理可得 AB∥CD,
∴四边形ABCD是平行四边形。
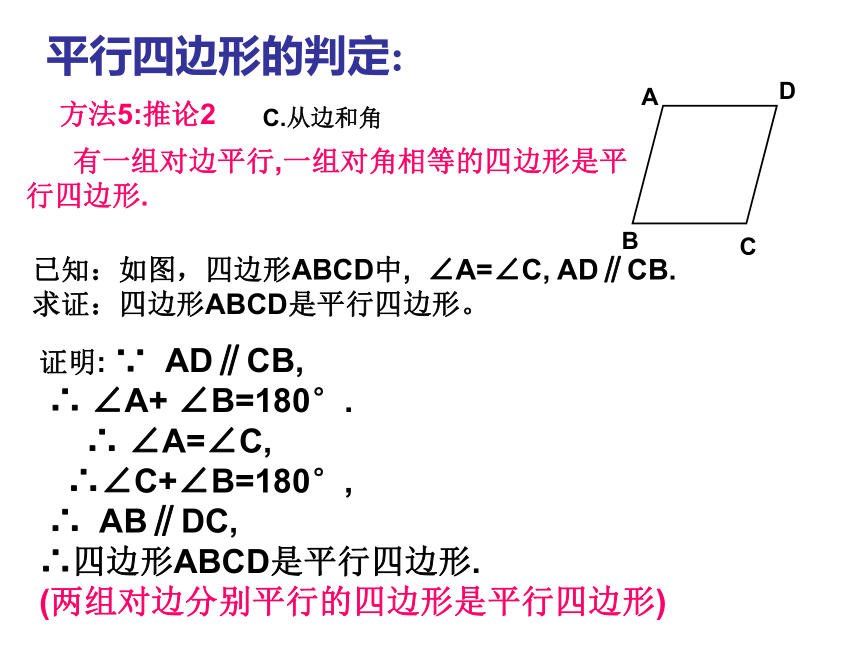
(两组对边分别平行的四边形是平行四边形) 平行四边形的判定:C.从边和角 有一组对边平行,一组对角相等的四边形是平行四边形.方法5:推论2已知：如图，四边形ABCD中, ∠A=∠C, AD∥CB.
求证：四边形ABCD是平行四边形。证明: ∵ AD∥CB,
∴ ∠A+ ∠B=180°.
∴ ∠A=∠C,
∴∠C+∠B=180°,
∴ AB∥DC,
∴四边形ABCD是平行四边形.
(两组对边分别平行的四边形是平行四边形) 平行四边形的判定:∴四边形ＡＢＣＤ是平行四边形.平行四边形判定定理3： 如图,在四边形ABCD中,
对角线AC,BD相交于点O,
∵OA=OC，OB=OD（对角线互相平分的四边形是平行四边形）D对角线：平行四边形的判定:1、在　ABCD中，已知AB=5,
　BC=3,则CD=____,AD=___。
2、在　ABCD中，已知∠A＝　　　　　　　
　　50°，则∠B＝　　　，
∠C＝　　　，∠D＝　　　。
53130°50°130°3如图所示，四边形ABCD是平行四边形
1）若周长为30㎝，CD＝6 ㎝，则AB＝ ㎝；
　 BC＝ 　　　㎝；AD＝ ㎝。
2）若∠A＝70°，则∠B＝　 。∠C＝ 　　； ∠D＝ 。
3）若∠A＋∠C=80°，则∠A＝ ；∠D＝ 。3. 在 ABCD中, ∠A:∠B=2:7,
则∠C= 度.
4. 已知 ABCD的周长为30㎝,
AB:BC=2:3, 则AB= ㎝.小试牛刀406在　　ABCD中
1、若∠ABC=65°∠CAD=60°，
则∠D= 　°；∠ACD= °；
∠BAC= °。2、若AC⊥AB，若BC=10㎝，AC=8㎝
则AD= ㎝；AB= ㎝；
DC= ㎝。5.如图:在 ABCD中，已知AC=3cm, ABC的周长为8cm,求平行四边形的周长DACBFE 3. 如图: 在 ABCD中,∠BAD = 2∠B, ∠BCD的平分线交BA的延长线于点E,
则△EBC是 三角形.ABCEFD120°60°60°60°正初露锋芒4.如图: 在 ABCD中, ∠DAB的平分线
AE交CD于点E, BC=9，AB=15，

则 CE= .
ABCDE1236初露锋芒915915965.如图: 在△ABC中, AB = AC = 8,
点D 在BC上, DE∥AC交AB于点E, DF∥AB交AC于F,
则DE＋DF = .ABCDEF18初露锋芒6.判断下列四边形是不是平行四边形?是是是是我 能 行!再展雄姿7. 如图:在 ABCD中, 对角线AC、BD
交于点O,
ABCDO(A) (B)
(C) (D) 2 3

4 5EF则图中共有( )对全等三角形. 6
7 8CBEF过O交AD于E，交BC于F，AB=5， BC=6， OE=2， 则四边形EFCD的周长是 ( ) 13
15 17C55228. 如图： 平行四边形ABCD中,
AC、BD相交于点O, AB=8, △AOB的面积为 ,ABCD的面积为 .ABCDO2424968610 4, 12 B. 6, 8
C. 8, 26 D. 12, 20则以下列两条线段长为对角线的长,
能组成平行四边形的是( )DAC=12, BD=20.则△AOB的周长为再展雄姿2634413三角形奠基法9、画平行四边形如：画一个平行四边形ABCD，使边BC=5cm,
对角线AC=5cm，BD=8cm.小试牛刀xyO123-1-27213-1-2-3-3410.如图，Rt△OAB的两条直角边在坐标轴上，已知点A（0，2），点B（3，0），则以点O,A,B为其中三个顶点的平行四边形的第四个顶点C的坐标为______。ABO-4大显身手证明:在 ABCD中,
AD ∥ BC
=∴ = A D
B CEF A D
B CEFEF D C
A BEFAE BFDE BFABFEEBFDAE CFAFCE∵E、F分别是AD、BC的中点∥ ∵BF = DE∴四边形 是平行四边形.探索规律证明: 在 ABCD中,
AB∥CD
∴∠1 = ∠2
又∵AE = CF
∴△ABE≌△CDF(SAS)
∴BE = DF同理 DE = BF
∠3=∠4∴∠5=∠6∴BE∥DF∴四边形 是平行四边形.123456ABCDEFFGHOOOEFGHEF=O证明: 在 ABCD中，
OA = OC， OB = OD∵ AE = CF
∴OA AE=OC CF
即 OE = OF－－＋＋BG = DHOB BG=OD DHOG = OH＋＋－ － A D
B C A D
B C A D
B CEBEDFEGFH探索规律EFBADCGHO如图: 在 ABCD中, AC、BD交于点O, 延长AC至F, 反向延长AC至E, 使AE=CF, 过点O画GH交AD于G, 交BC于H, 连结EH、HF、FG、GE,
求证: 四边形EHFG是平行四边形.证明: 在 ABCD中AD∥BC, OA=OC,∴∠1=∠2, ∠3=∠4,∴△AOG≌△COH∴ OG = OH又∵ AE=CF∴ OE=OF∴四边形EHFG是平行四边形.1234我也会做如图; 在 ABCD中, 以AD、BC为边作
正三角形ADE, 正三角形BCF, 连结BE,DF,
求证: 四边形EBFD是平行四边形.ABCDEF1234证明: 在 ABCD中,AD = BC, AB = CD,∠1 = ∠2∵△ADE与△BCF都是正三角形,∴AE=DE=AD, BE=CF=BC,
∠3=∠4=60°.∴DE=BF, AE=CF,
∠1＋∠3=∠2＋∠4,即 ∠EAB=∠DCF,∴△ABE≌△DCF∴BE=DF∴四边形EBFD是平行四边形.合作探究
通过这节课的学习，
你有哪些收获？
能与大家一起分享吗？丰 收 园