2.4二次函数的应用（2）

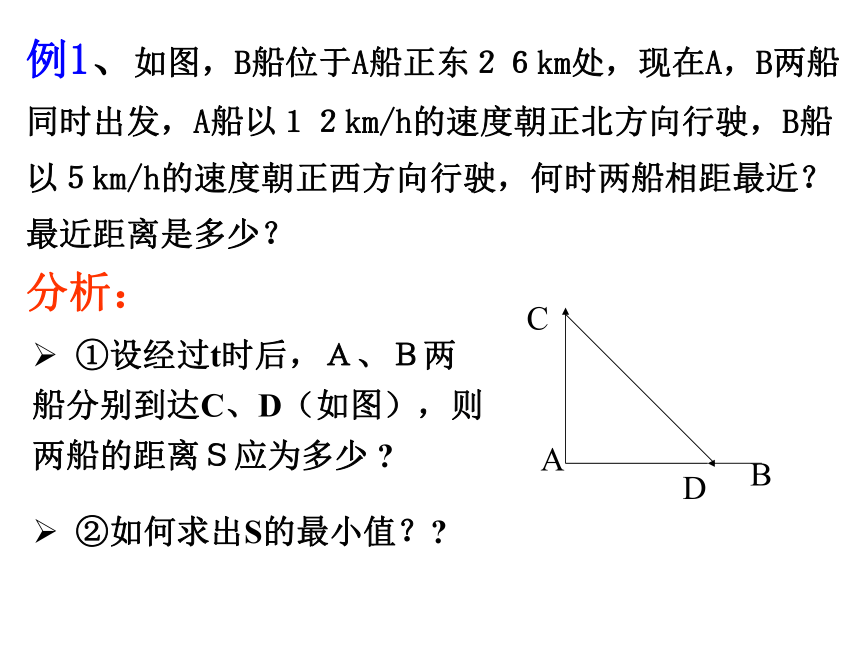
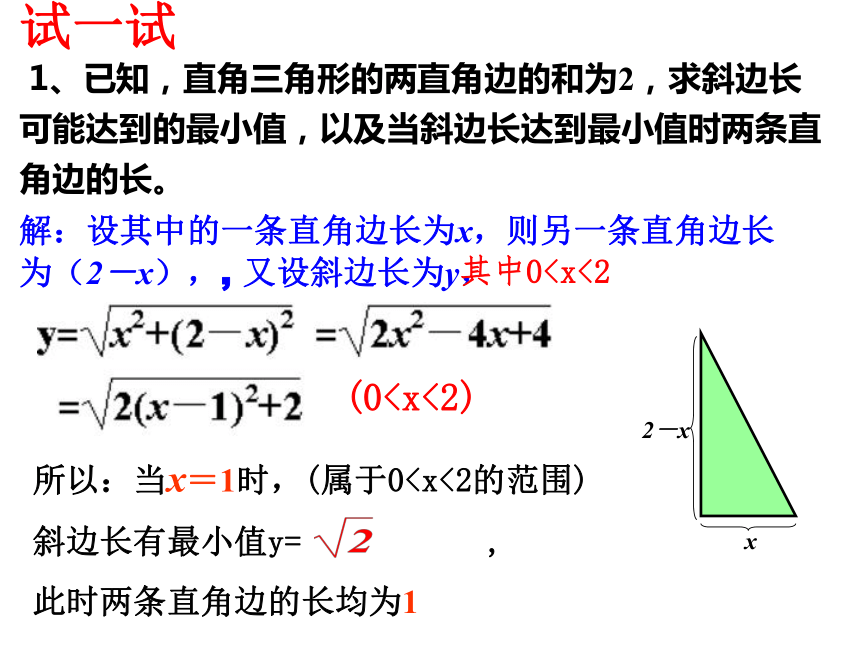
课件19张PPT。2.4 二次函数的应用(2)想一想如何求下列函数的最值：例1、如图，B船位于A船正东２６km处，现在A，B两船同时出发，A船以１２km/h的速度朝正北方向行驶，B船以５km/h的速度朝正西方向行驶，何时两船相距最近？最近距离是多少？ ①设经过t时后，Ａ、Ｂ两船分别到达C、D（如图），则两船的距离Ｓ应为多少 ?分析： ②如何求出S的最小值？?解：设经过t时后，两船的距离为S，则：（t＞0）即S有最小值24km答：略。归纳小结 运用二次函数的性质求实际问题的最大值和最小值的一般步骤 :求出函数解析式和自变量的取值范围配方变形，或利用公式求它的最大值或最小值。检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内 。 1、已知，直角三角形的两直角边的和为2，求斜边长可能达到的最小值，以及当斜边长达到最小值时两条直角边的长。解：设其中的一条直角边长为x，则另一条直角边长为（2－x），, 又设斜边长为y，所以：当x＝1时，(属于0斜边长有最小值y= ,
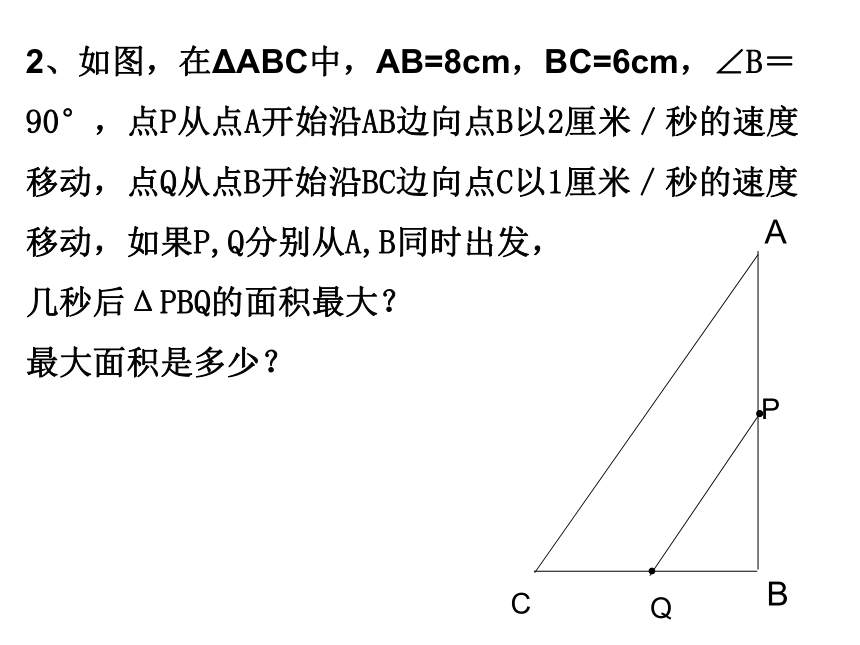
此时两条直角边的长均为1其中0移动，如果P,Q分别从A,B同时出发，
几秒后ΔPBQ的面积最大？
最大面积是多少？3、某商场将进价40元一个的某种商品按50元一个售出时，能卖出500个，已知这种商品每个涨价一元，销量减少10个，为赚得最大利润，售价定为多少？最大利润是多少？分析：利润=（每件商品所获利润）× （销售件数）解：设每个涨价x元， 那么（3）销售量可以表示为 ；（1）销售价可以表示为 ；（50+x）元(500-10x) 个（2）一个商品所获利润可以表示为 ；（50+x-40）元（4）共获利润可以表示为 ；(50+x-40)(500-10x)元例2、某饮料经营部每天的固定成本为200元，其销售的饮料每瓶进价为5元。销售单价与日均销售量的关系如下：①若记销售单价比每瓶进价多x元，日均毛利润（毛利润=售价-进价-固定成本）为y元，求y关于x的函数解析式和自变量的取值范围；②若要使日均毛利润达到最大，销售单价应定为多少元（精确到０.１元）？最大日均毛利润为多少元？解（1）由题意，销售单价每增加1元，日均销售量就减少40瓶，当销售单价比进价多x元时，与销售单价6元相比，日均销售量为：480-40（x+5-6）=（520-40x）瓶由520-40x＞0，得x＜13，即0＜x＜13∴所求的函数解析式为y=（520-40x）x-200即，y=-40x2+520x-200 （0＜x＜13）（2）由（1）得，y=-40（x-6.5）2+1490 （0＜x＜13） 当x=6.5时，函数y达到最大值1490，而x=6.5满足取值条件∴当销售 单价定为11.5元时，日均毛利润最大，为1490元。答：略。1、某广告公司设计一幅周长为12m的矩形广告牌，
广告设计费为每平方米1000元，设矩形一边长为
X(m)，面积为S(m2)。 (1)求出S与x之间的函数关系式，并确定自
变量的取值范围。(2)请你设计一个方案，使获得的设计费最多。练一练 2、有一种大棚种植的西红柿，经过实验，其单位面积的产量与这个单位面积种植的株数成构成一种函数关系。每平方米种植4株时，平均单株产量为2kg；以同样的栽培条件，每平方米种植的株数每增加1株，单株产量减少1/4kg。
问每平方米种植多少株时，能获得最大的产量？最大的产量为多少？练一练例3、如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围；
(2)当x取何值时所围成的花圃面积最大，最大值是多少？
(3)若墙的最大可用长度为8米，则求围成花圃的最大面积。解： (1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为（24－4x）米 (3) ∵墙的可用长度为8米∴ S＝x（24－4x）
＝－4x2＋24 x （0则 y=60-x2 -（10-x）（6-x）=-2x2 + 16x（0 的一部分(如图)，若命中篮圈中心，则他与篮底的距离L以及投篮时手离地面的高度分别是多少？做一做1、通过这节课的学习活动你有哪些收获？2、对这节课的学习，你还有什么想法吗？感悟与反思 1、如图所示，已知抛物线y=ax2+bx+c(a≠0)与x轴相交于两点A（x1，0） B（x2，0）（x1 已知有一张边长为10cm的正三角形纸板，若要从中剪一个面积最大的矩形纸板，应怎样剪？最大面积为多少？再见