2.4二次函数的应用（3）

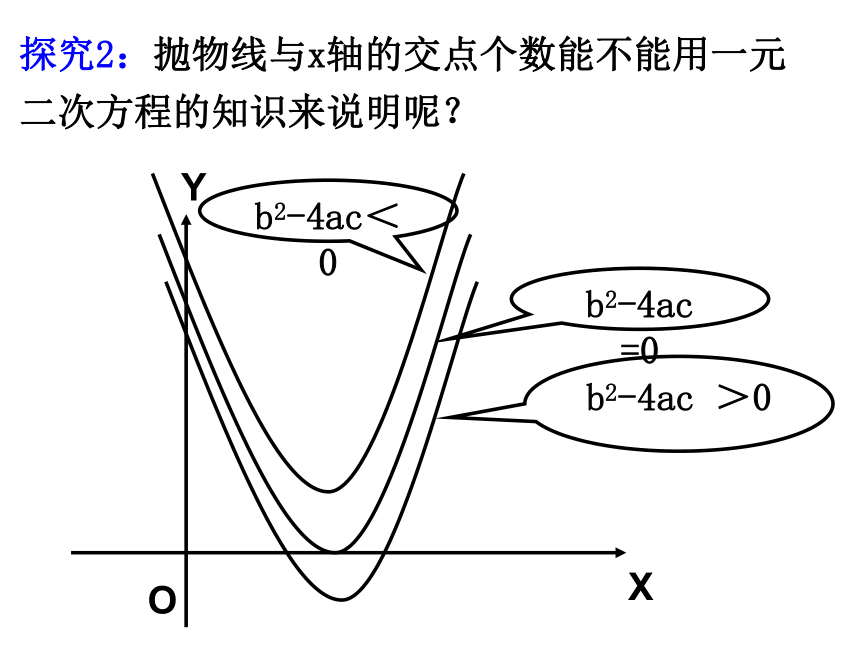
课件26张PPT。2.4 二次函数的应用(3)温故知新由b2-4ac的符号决定b2-4ac﹥0，有两个交点b2-4ac=0，只有一个交点b2-4ac﹤0，没有交点 如何求二次函数图象的顶点坐标，与x轴的交点坐标，与y轴的交点坐标？二次函数的图象与x轴有没有交点，由什么决定?探究1：求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标。解：∵A、B在x轴上，
∴它们的纵坐标为0，
∴令y=0，则x2-3x+2=0
解得：x1=1，x2=2；
∴A（1，0） ， B（2，0） 你发现方程 的解x1、x2与A、B的坐标有什么联系？x2-3x+2=0合作学习结论1：方程x2-3x+2=0的解就是抛物线y=x2-3x +2与x轴的两个交点的横坐标。因此，抛物线与一元二次方程是有密切联系的。即：若一元二次方程ax2+bx+c=0的两个根是x1、x2，则抛物线y=ax2+bx+c与轴的两个交点坐标分别是A（ ）， B（ ）x1，0x2，0x探究2：抛物线与x轴的交点个数能不能用一元二次方程的知识来说明呢？b2-4ac ＞0b2-4ac =0
b2-4ac＜0OXY结论2：抛物线y=ax2+bx+c抛物线y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明： 1、 b2-4ac ＞0 一元二次方程ax2+bx+c=0
有两个不等的实数根与x轴有两个交点——相交。抛物线y=ax2+bx+c 2、 b2-4ac =0 一元二次方程ax2+bx+c=0
有两个相等的实数根与x轴有唯一公共点——相切（顶点）。抛物线y=ax2+bx+c 3、 b2-4ac ＜0 一元二次方程ax2+bx+c=0
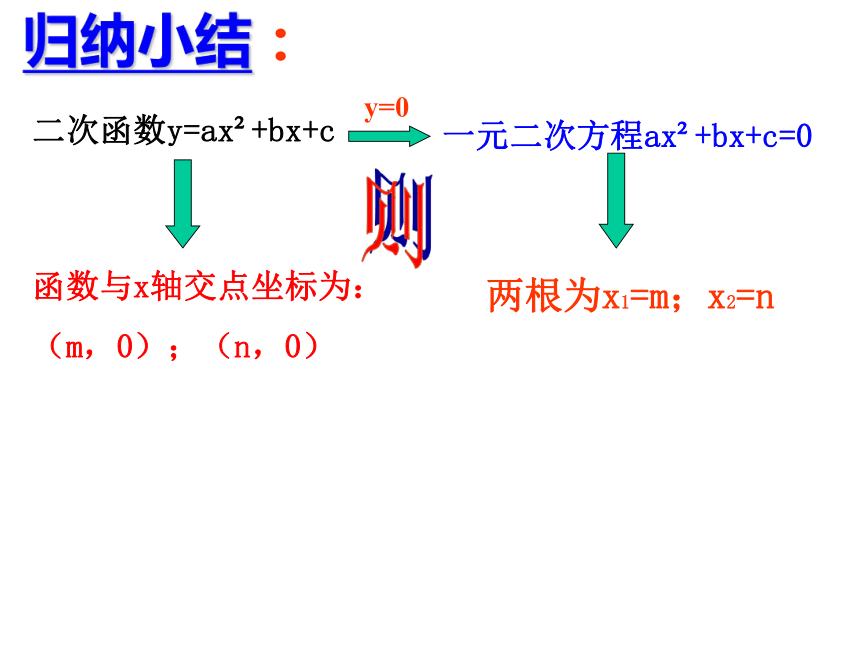
没有实数根与x轴没有公共点——相离。二次函数y=ax2+bx+c 归纳小结：一元二次方程ax2+bx+c=0两根为x1=m；x2=n则函数与x轴交点坐标为：
（m，0）；（n，0）1、已知抛物线y=x2-6x+a的顶点在x轴上，则a= ；若抛物线与x轴有两个交点，则a的范围是 ；若抛物线与坐标轴有两个公共点，则a的范围是 ；3、已知抛物线y=x2+px+q与x轴的两个交点为（-2，0），（3，0），则p= ，q= 。2、已知抛物线y=x2-3x+a+1与x轴最多只有一个交点，则a的范围是 。做一做4、判断下列各抛物线是否与x轴相交，如果相交，求出交点的坐标。
（1）y=6x2-2x+1 （2）y=-15x2+14x+8
（3）y=x2-4x+45、抛物线y=ax2+bx+c（a≠0）的图象全部在轴下方的条件是（ ）
（A）a＜0 b2-4ac≤0 （B）a＜0 b2-4ac＞0
（C）a＞0 b2-4ac＞0 （D）a＜0 b2-4ac＜0D例1： 一个球从地面上竖直向上弹起时的速度为10m/s，经过t（s）时球的高度为h（m）。已知物体竖直上抛运动中，h=v0t－ ? gt2（v0表示物体运动上弹开始时的速度，g表示重力系数，取g=10m/s2）。问球从弹起至回到地面需要多少时间？经多少时间球的高度达到3.75m?地面解：由题意，得h关于t的二次函数
解析式为h=10t-5t2取h=0，得一元二次方程
10t－5t2=0解方程得t1=0，t2=2球从弹起至回到地面需要时间为t2－t1=2（s）取h=3.75，得一元二次方程10t－5t2=3.75解方程得t1=0.5；t2=1.5答：球从弹起至回到地面需要时间为2（s）；
经过0.5s或1.5s球的高度达到3.75m。例1：1、一球从地面抛出的运动路线呈抛物线，如图，当球离抛出地的水平距离为 30m 时，达到最大高10m。
⑴ 求球运动路线的函数解析式和自变量的取值范围；
⑵ 求球被抛出多远；
⑶ 当球的高度为5m时，球离抛出地面的水平距离
是多少m？练一练p50t1练一练2、某拱形门建筑的形状是抛物线，若取拱形门地面上两点的连线为x轴，它可以近似地用函数y=- （x-97）2 +194表示（单位：m），问拱形门大约有多宽？有多高？p51t3 利用二次函数的图象求一元二次方程
X2+X－1= 0 的近似解。例2、做一做 ◆用求根公式求出方程x2+x-1=0的近似解，并由检验例2中所给图象解法的精确度。 在例2中，我们把一元二次方程X2+X－1= 0 的解看做是抛物线y=x2+x-1与x轴交点的横坐标，利用图象求出了方程的近似解。如果把方程x2+x-1 = 0变形成 x2 = -x+1，那么方程的解也可以看成怎样的两个函数的交点的横坐标？用不同图象解法试一试，结果相同吗？在不使用计算机画图象的情况下，你认为哪一种方法较为方便？探究活动：做一做 ◆利用函数图象判断下列方程有没有解，有几个解。若有解，求出它们的解（精确到0.1）。
①X2=2x-1 ②2x2-x+1=0 ③2x2-4x-1=01、已知抛物线y=x2+2x+m+1。
（1）若抛物线与x轴只有一个交点，求m的值。
（2）若抛物线与直线y=x+2m只有一个交点，求m的值。练一练2、已知抛物线y=ax2+bx+c的顶点为（1，-4）与x轴两交点坐标分别为（x1，0），（x2，0），且x12+x22=10，求抛物线的解析式。y=x2-2x-3小结：1、若一元二次方程ax2+bx+c=0的两个根是x1、x2， 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A（x1，0 ）， B（ x2，0 ）3、A、B两点间的距离AB= 。2、一元二次方程ax2+bx+c=0与二次三项式ax2+bx+c及二次函数y=ax2+bx+c这三个“二次”之间互相转化的关系。体现了数形结合的思想。3、已知是x1、x2方程x2-（k-3）x+k+4=0的两个实根，A、B为抛物线y= x2-（k-3）x+k+4与x轴的两个交点，P是y轴上异于原点的点，设∠PAB=α，∠PBA=β，问锐角α、β能否相等？并说明理由.αβ解：已知α、β都是锐角，则A、B两点在原点的两侧，故x1、x2必异号， ∴ x1x2＜0， 即k+4＜0，∴k＜- 4.若α=β,则OA=OB,即-x1=x2,即x1+x2=0∴k-3=0, ∴ k=3,这与k＜-4矛盾∴α≠β拓展提高1、已知命题：若二次函数y=ax2+bx+c（a≠0）的图象与x轴交于（x1，0），（x2，0）两点， 则y=a（x-x1）（x-x2）。判断这个命题的真假，并说明理由。2、已知二次函数y=x2-kx-2+k.
(1)求证:不论k取何值时，这个二次函数
y=x2-kx-2+k与x轴有两个不同的交点。
(2)k为何值时,二次函数y=x2-kx-2+k与x轴两个交点A、B之间的距离最小？
（3）设此抛物线与y轴的交点为C，当k为6时,求S△ABC .拓展提高3、已知抛物线y=x2-（m2+8）x+2（m2+6）.
(1)求证:不任m为何实数,抛物线与x轴都有两个不同的交点,且这两个交点都在x轴的正半轴上.
(2)设抛物线与y轴交于点A,与x轴交于B、C两点（点B在点C的左侧），求点A、B、C的坐标
（用m的代数式表示）。
（3）若△ABC的面积为48平方单位，求m的值。4、已知抛物线y=-x2+2（m+1）x+m+3与x轴有两个交点A、B，其中A在x轴的正半轴，B在x轴的负半轴，（1）若OA=3OB，求m的值。
解：设B点坐标为（-X，0），则A点坐标为（3X，0），
又由根与系数关系可知，
-X+3X＝2（m+1）
-X×3X＝-（m+3）
解方程组得：m=0, 或m＝
因为有两交点，则b2-4ac ＝
把m=0, 或m＝ 代入均可使△＞0成立，
所以m=0, 或m＝ 。4、已知抛物线y=-x2+2（m+1）x+m+3与x轴有两个交点A、B，其中A在x轴的正半轴，B在x轴的负半轴，（1）若OA=3OB，求m的值。
（2）若3（OA-OB）=2OA·OB，求m的值。同学们，再见！