2.7直角三角形的判定

课件24张PPT。判断三角形全等条件三边对应对应相等 SSS
两角及其夹边对应相等 ASA
两角及其中一角的对边对应相等 AAS
两边及其夹角对应相等 SAS
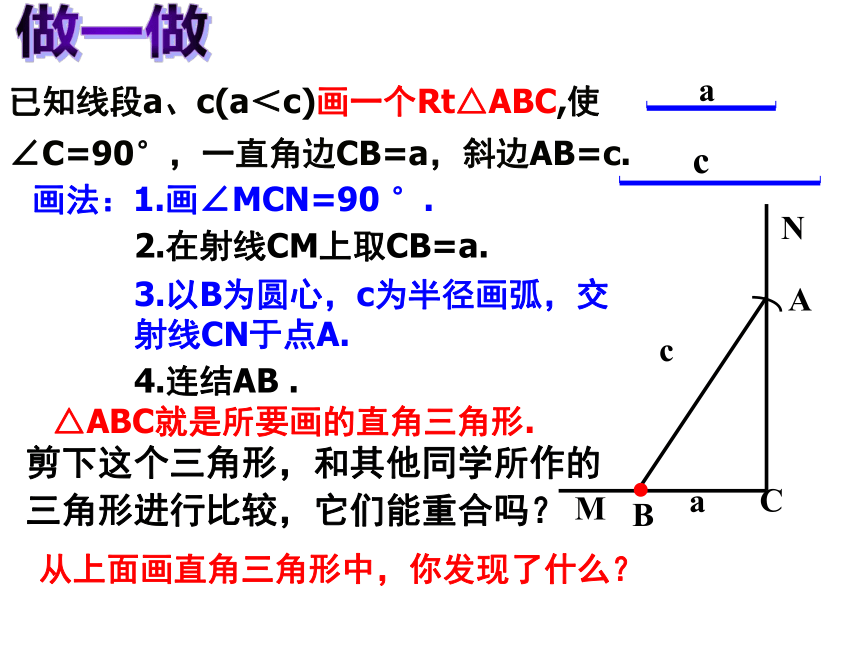
1．三角形全等的判定定理有哪些? 复习旧知2.7 直角三角形全等的判定做一做：如图，具有下列条件的Rt△ABC和Rt△A’B’C’是否全等： 探索新知2．有两条边对应相等的两个三角形全等吗? 已知线段a、c(a＜c)画一个Rt△ABC,使∠C=90°，一直角边CB=a，斜边AB=c.画法：1.画∠MCN=90 °. 3.以B为圆心，c为半径画弧，交射线CN于点A. 4.连结AB . △ABC就是所要画的直角三角形. MCNaBcA2.在射线CM上取CB=a. 做一做从上面画直角三角形中，你发现了什么？ 剪下这个三角形，和其他同学所作的
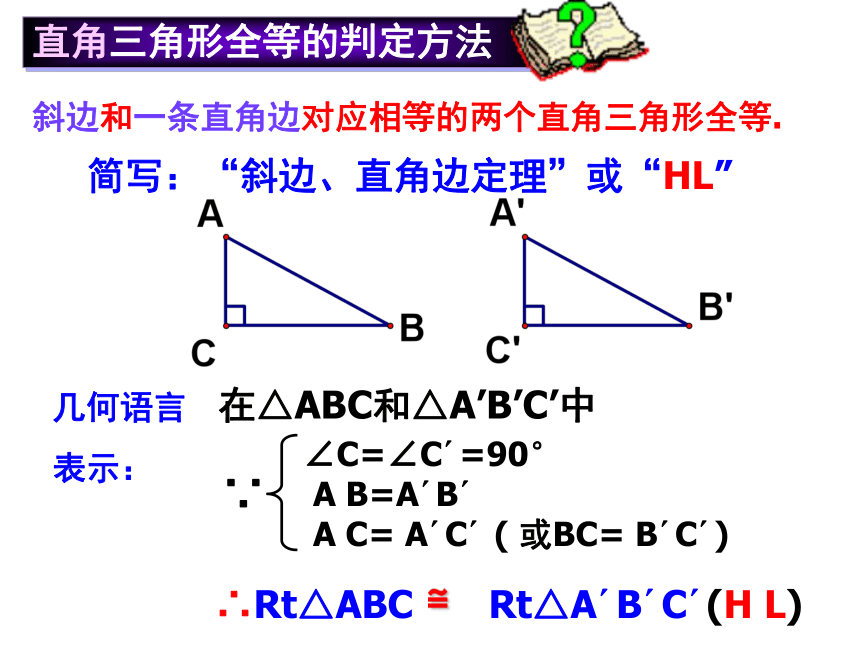
三角形进行比较，它们能重合吗？ 简写：“斜边、直角边定理”或“HL”∠C=∠C′=90°
A B=A′B′
A C= A′C′ ( 或BC= B′C′) ∴Rt△ABC ≌ Rt△A′B′C′(H L) 直角三角形全等的判定方法 ∵ 几何语言
表示： 斜边和一条直角边对应相等的两个直角三角形全等.在△ABC和△A’B’C’中 如图，在△ABC和△A’B’C’中，
∠C= ∠C’=Rt∠，AB=A’B’，AC=A’C’
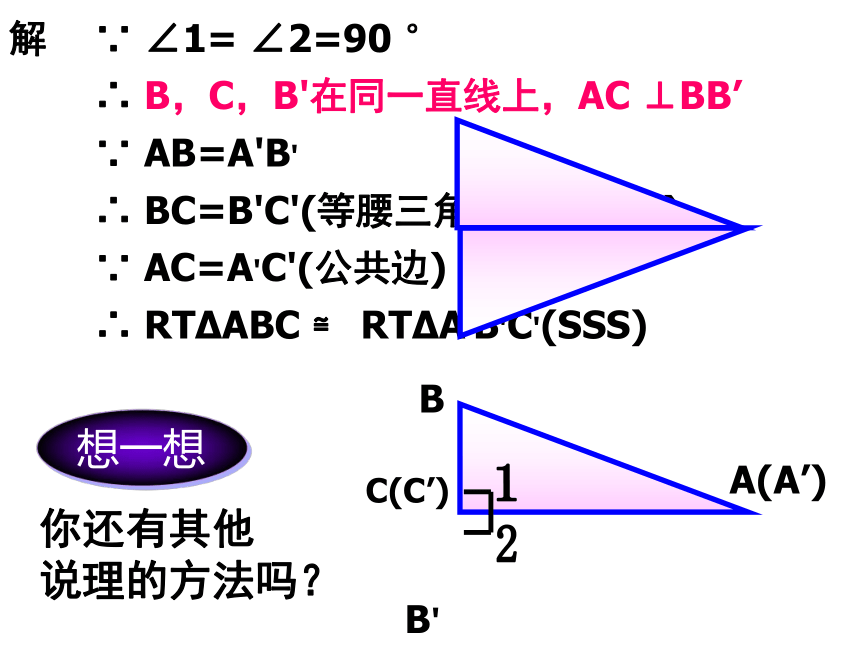
说明△ABC和△A’B’C’ 全等的理由。 验证 斜边、直角边定理 解 ∵ ∠1= ∠2=90 °
∴ B，C，B'在同一直线上，AC ⊥BB’
∵ AB=A'B'
∴ BC=B'C'(等腰三角形三线合一)
∵ AC=A'C'(公共边)
∴ RTΔABC ≌ RTΔA'B'C'(SSS)
12BC(C’)B'A(A’)
想一想你还有其他
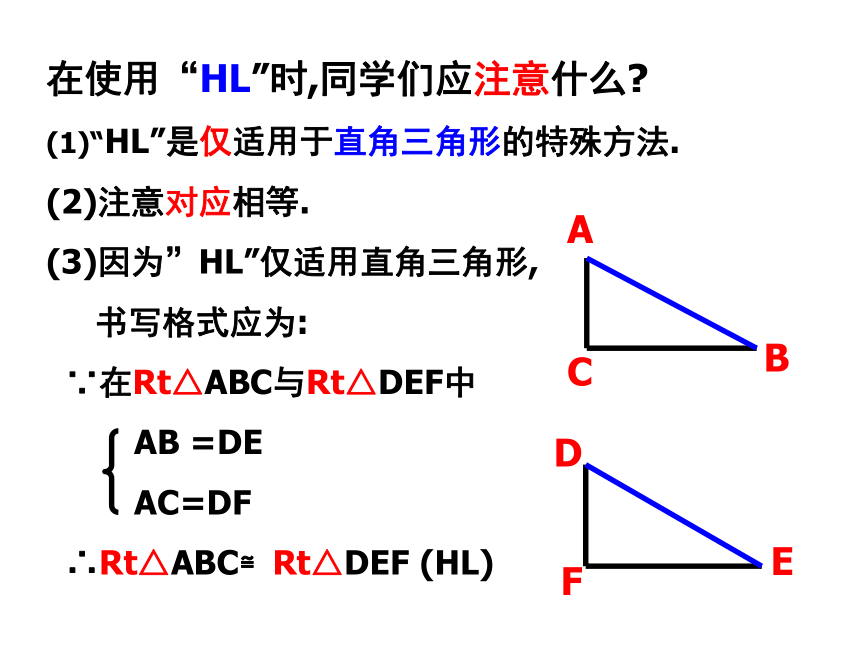
说理的方法吗？ 在使用“HL”时,同学们应注意什么?
“HL”是仅适用于直角三角形的特殊方法.
注意对应相等.
因为”HL”仅适用直角三角形,
书写格式应为:
∵在Rt△ABC与Rt△DEF中
AB =DE
AC=DF
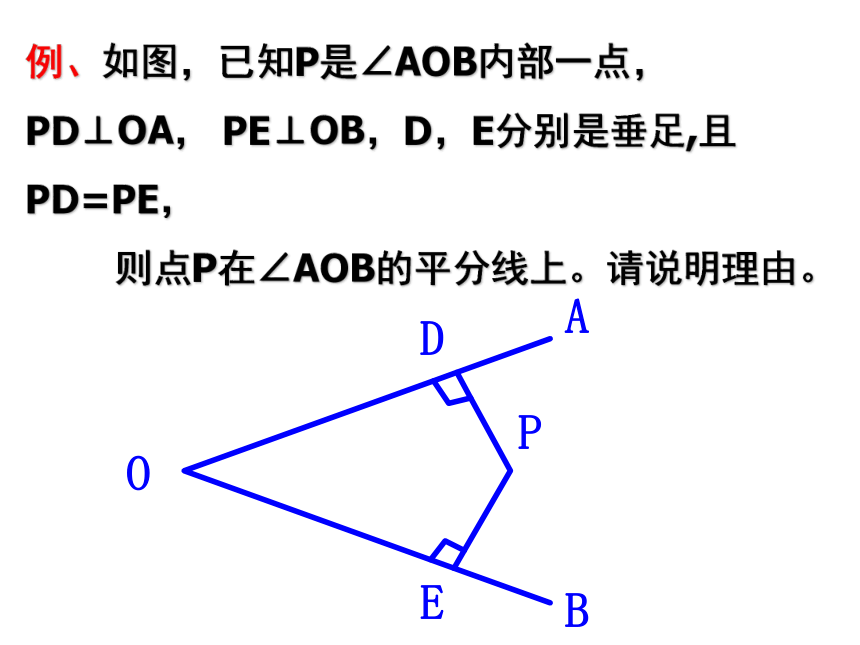
∴Rt△ABC≌Rt△DEF (HL)例、如图，已知P是∠AOB内部一点，PD⊥OA， PE⊥OB，D，E分别是垂足,且PD=PE，
则点P在∠AOB的平分线上。请说明理由。判断直角三角形全等条件三边对应相等 SSS
一锐角和它的邻边对应相等 ASA
一锐角和它的对边对应相等 AAS
两直角边对应相等 SAS
斜边和一条直角边对应相等 HL 直角三角形是特殊的三角形，所以不仅有一般三角形判定全等的方法，还有直角三角形特有的判定方法“HL”.小 结你能够用哪几种方法说明两个直角三角形全等？我们应根据具体问题的实际情况选择判断两个直角三角形全等的方法.1.已知:如图,D是△ABC的BC边上的中点,
DE⊥AC，DF⊥AB,垂足分别为E,F,且DE=DF. 求证: △ABC是等腰三角形.解：∵ DE⊥AB，DF⊥AC(已知)
∴ ∠ BED= ∠ CFD=RT ∠ (垂直意义)
∵ DE=DF(已知)
∵ BD=CD(中点意义)
∴ RT △BDE ≌ RT △CDF(HL)
∴∠B=∠ C(全等三角形对应角相等)
∴AB=AC(在一个三角形中，等角对等边) 课内练习2.如图，已知CE ⊥ AB，DF ⊥ AB，AC=BD，AF=BE，
求证：CE=DF。 AC∥BD吗？为什么？ 课内练习23.已知△ABC ，请找出一点P，使它到三边
的距离都相等
(只要求作出图形，并保留作图痕迹). 到三边的距离相等的点：
三角形的角平分线的交点。 P课内练习3直角三角形全等的判定定理:
SAS, AAS, ASA, SSS, HL
综上所述,直角三角形全等的判定条件可归纳为:
一边及一个锐角对应相等的两个直角三角形全等;
两边对应相等的两个直角三角形全等;
切记!!! 两边及其中一边的对角对应相等的两个三角形不一定全等.小结 拓展1、判断下列说法的正误,并说明理由:两个锐角对应相等的两个直角三角形全等;斜边及一个锐角对应相等的两个直角三角形全等; 两直角边对应相等的两个直角三角形全等;一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等.× √ √ √ 练一练： (1) _______,∠A=∠D ( ASA )
(2) AC=DF,________ (SAS)
(3) AB=DE,BC=EF ( )
(4) AC=DF, ______ (HL)
(5) ∠A=∠D, BC=EF ( )
(6) ________,AC=DF ( AAS ) 把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整. AC=DF BC=EF HL AB=DE AAS ∠B=∠E(2)若∠A=∠D，BC=EF，则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法)(3)若AB=DE，BC=EF，则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法)(4)若AB=DE，AC=DF则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法)2、如图，∠ABD与∠DEF都是直角(1)若∠A=∠D，AB=DE，则△ABC与△DEF (填“全等”或“不全等”)根据 (用简写法)全等 全等 全等 全等 ASA AAS SAS HL 3、如图，AC=AD，∠C=∠D=Rt∠ ，你能说明∠ABC与∠ ABD相等吗？解：BC=BD，理由如下： AB=AB,
AC=AD.∴ Rt△ACB≌Rt△ADB (HL) ∴BC=BD(全等三角形对应边相等) 在Rt△ACB和Rt△ADB中例2 、如图，在△ABC与△A’B’C’中， CD， C’D’分别是高，并且AC＝A’C’，CD＝C’D’，∠ACB＝∠A’C’B’．
求证：△ABC≌△A’B’C’．1、如图，两根长度为12米的绳子，一端系在旗杆上，另一端分别固定在地面两个木桩上，两个木桩离旗杆底部的距离相等吗？请说明你的理由。应用练习： 3、如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，两个滑梯的倾斜角∠ABC和∠DFE大小有什么关系？ 解：(1)∵在R t△ABC和Rt△DEF中 ∴ Rt△ABC≌Rt△DEF (HL)(2) ∵Rt△ABC≌Rt△DEF
∴∠ABC=∠DEF(全等三角形对应角相等) ∴∠ABC+∠DFE=90° 又∵∠DEF+∠DFE=90°
(直角三角形的两个锐角互余) 2、再过点M作OA的垂线,1、如图:在已知∠AOB的两边OA,OB上
分别取点M,N,使OM=ON;3、过点N作OB的垂线,两垂线交于点P,4、那么射线OP就是∠AOB的平分线.P●你能用一个三角板作任意角的角平分线吗？角平分线性质：角的内部，到角两边距离相等的点，在这个角的平分线上。