2.6勾股定理(一)

课件20张PPT。2.6探索勾股定理(1)合作探究例题精练体会分享布置作业合作学习温故而知新我们已掌握直角三角形的哪些性质?1.两个锐角互余.2.斜边上的中线等于斜边的一半.3. 30o的角所对的直角边等于斜边的一半.温故而知新 温故而知新合作学习1.作直角三角形,使其两条直角边长分别为 3cm和4cm; 6cm和8cm; 5cm和12cm
2.分别测量这三个直角三角形斜边的长.
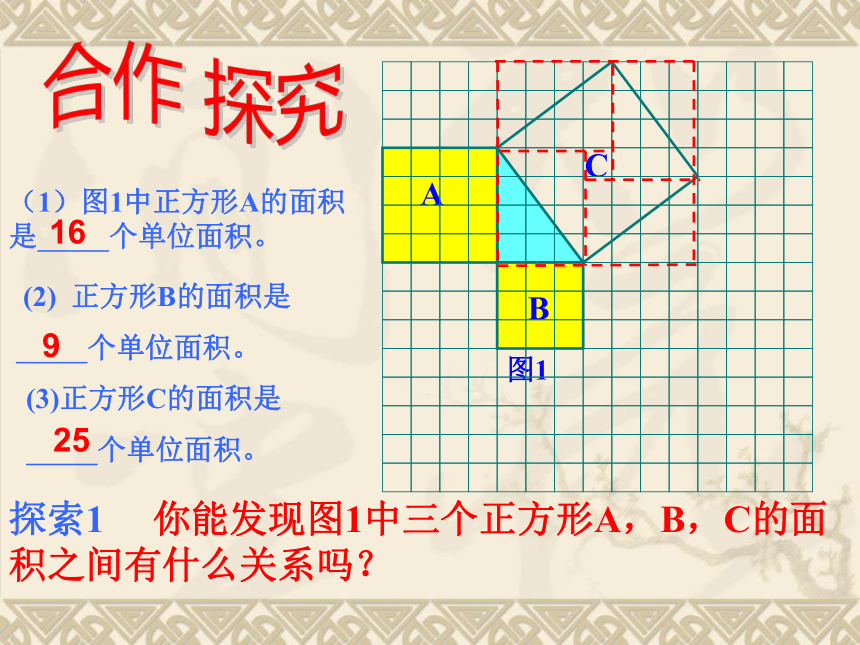
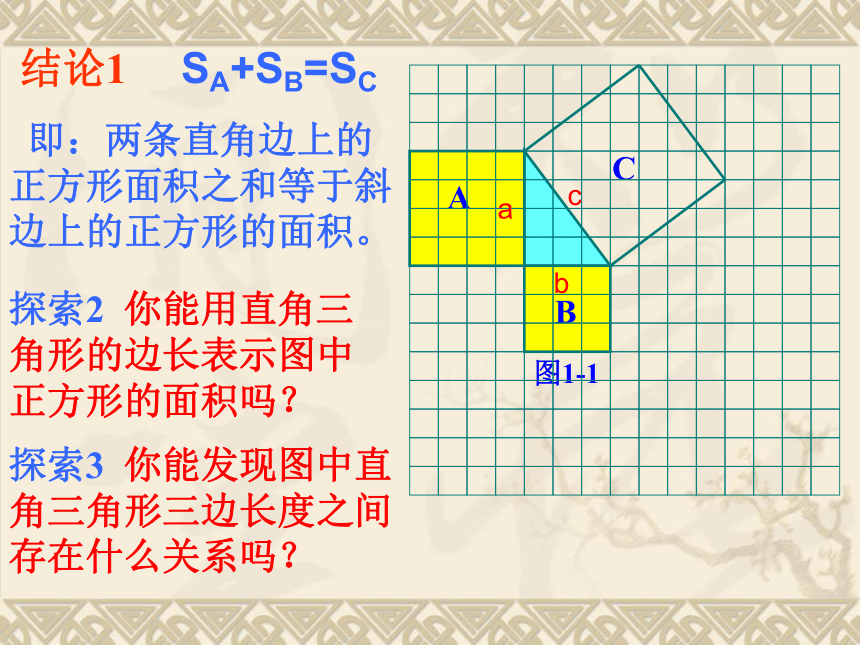
3.根据所测得的结果填写下表:525251010010013169169猜想：如果a、b为直角三角形的两条直角边长， c为斜边长，那么即直角三角形两直角边的平方和等于斜边的平方。 温故而知新（1）图1中正方形A的面积是 个单位面积。 (2) 正方形B的面积是
个单位面积。(3)正方形C的面积是
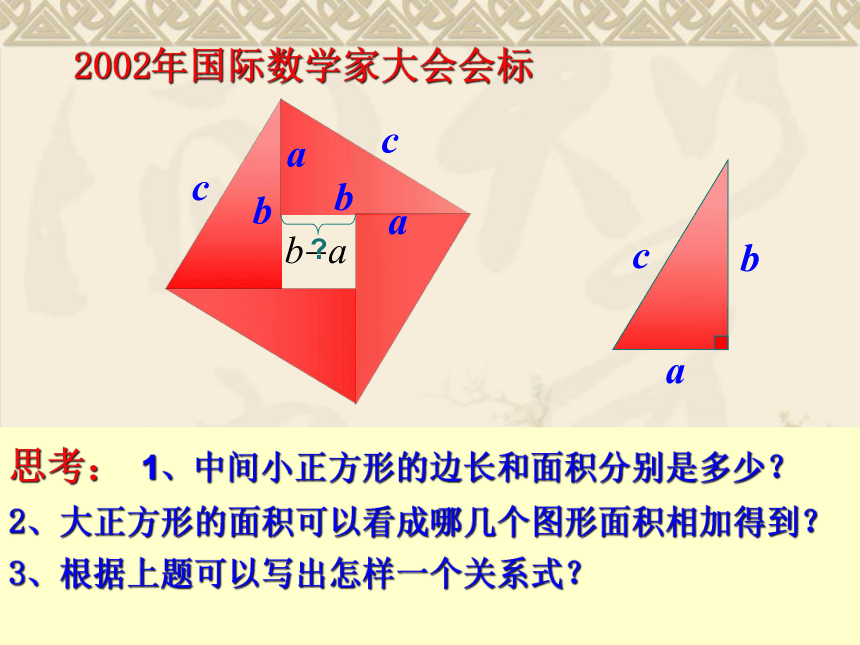
个单位面积。16925合作 探究探索1 你能发现图1中三个正方形A，B，C的面积之间有什么关系吗？ 结论1 SA+SB=SC 探索2 你能用直角三角形的边长表示图中正方形的面积吗？探索3 你能发现图中直角三角形三边长度之间存在什么关系吗？acb 即：两条直角边上的正方形面积之和等于斜边上的正方形的面积。利用拼图来探究勾股定理的正确性：1、准备四个全等的直角三角形（设直角三角形的两条直角边分别为a，b，斜边c）；2、你能用这四个直角三角形拼成一个正方形吗？拼一拼试试看3、你拼的正方形中是否含有以斜边c为边的正方形？4、你能否就你拼出的图说明a2+b2=c2？2002年国际数学家大会会标思考： 1、中间小正方形的边长和面积分别是多少？
2、大正方形的面积可以看成哪几个图形面积相加得到？
3、根据上题可以写出怎样一个关系式？
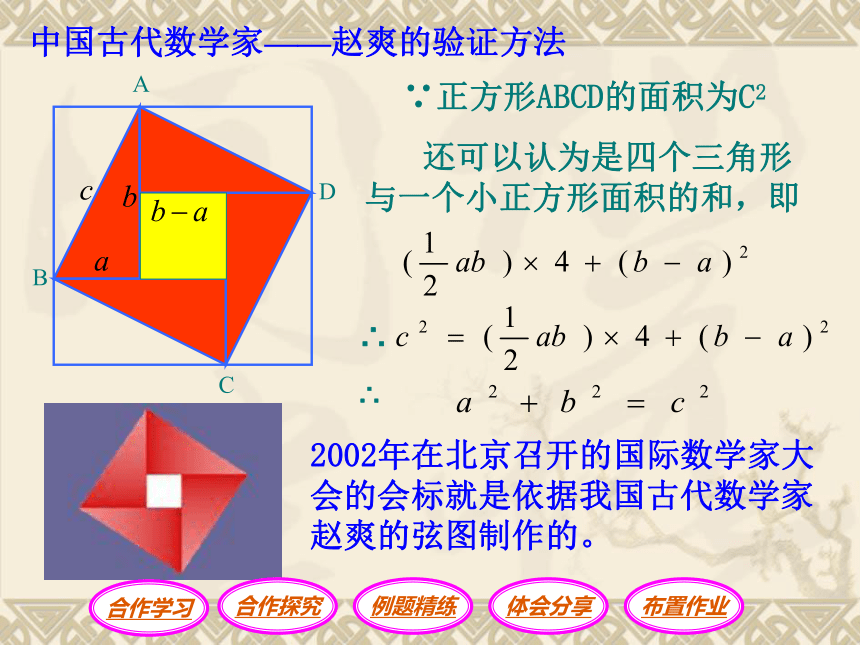
?中国古代数学家——赵爽的验证方法 还可以认为是四个三角形与一个小正方形面积的和，即∴2002年在北京召开的国际数学家大会的会标就是依据我国古代数学家赵爽的弦图制作的。∴ ∵正方形ABCD的面积为C2思维拓展 温故而知新勾股定理 如果直角三角形两直角边分别为a、b, 斜边为c，那么即 直角三角形两直角边的平方和等于斜边的平方。abc勾股弦bac 温故而知新在中国古代，人们把弯曲成直角的手臂的上半部分称为"勾"，下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.读一读 勾股世界
我国是最早了解勾股定理的国家之一。早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角三角形，如果勾等于三，股等于四，那么弦就等于五。即“勾三、股四、弦五”。它被记载于我国古代著名的数学著作《周髀算经》中。在这本书中的另一处，还记载了勾股定理的一般形式。
1945年，人们在研究古巴比伦人遗留下的一块数学泥板时，惊讶地发现上面竟然刻有15组能构成直角三角形三边的数，其年代远在商高之前。
相传二千多年前，希腊的毕达哥拉斯学派首先证明了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯定理。x例1：如图，你能计算出下列直角三角形中未知边的长吗？2 反思：若要你在数轴上准确表示 ，你会参考上面的结果画吗？小结：利用勾股定理可以
解决直角三角形的边长。121x83x5x例题精练解:由勾股定理得x2=12+22=5∵x>0
∴x=(1)直角三角形的两直角边为3和4,则斜边为___(3)直角三角形的两直角边为6和8,则斜边为___(2)直角三角形的两直角边为5和12,则斜边为___比一比谁最快(5)直角三角形的两条边为3和4，则斜边上的高是 。(4)直角三角形的两条边为3和4，则这个直角三角形的周长为 。12或51013 温故而知新例2：一个长方形零件图,根据所给的尺寸(单位mm),求两孔中心A、B之间的距离.C解：过A作铅垂线，过B作水平线,两线交于点C，则∠ACB=90°AC=90-40=50(mm)由勾股定理，得∵AB﹥0， ∴AB=130(mm)答：两孔中心A、B之间的距离为130mm。 构造直角三角形可以解决实际问题。BC=160-40=120(mm)50120 温故而知新 小刚想知道学校旗杆的高度，他发现旗杆上的绳子垂到地面还多1米，当他把绳子的下端拉开5米后，发现下端刚好接触到地面，你能计算旗杆的高度是多少米吗？试 一 试 温故而知新(1)求墙的高度? （精确到0.1米）解：∴AC=∵∠ACB=90°AB=3，BC=1==≈2.8(米)(2)若梯子的顶端下滑50厘米,
底端将向外水平移动多少米?AA′BB′3m1mC∴ AB2=AC2+BC2 有一架3米长的梯子靠在学校围墙上,刚好与墙头对齐,此时梯脚B与墙脚C的距离是1米。探究 温故而知新说说这节课你的收获和体会
让大家与你一起分享体会 . 分享作业1、阅读课本P43
2、完成作业本 温故而知新