相似三角形复习1

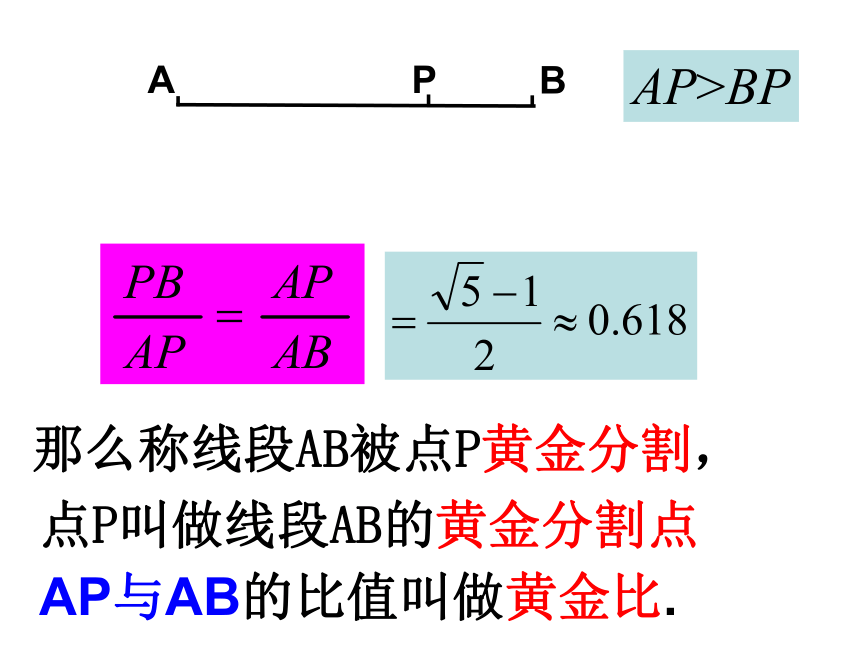
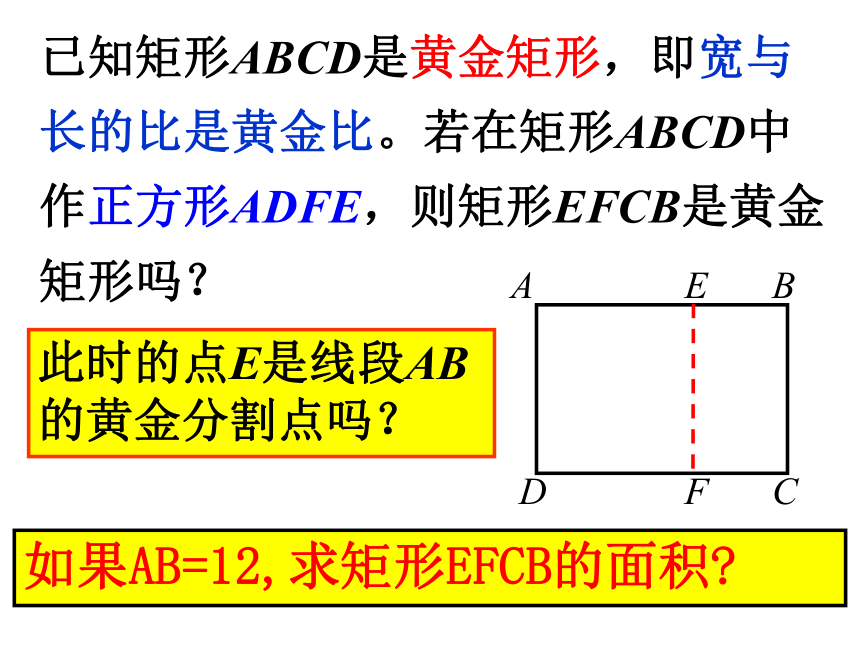
课件18张PPT。相似三角形复习已知四个数a、b、c、d ，如果或 a：b=c：d，我们说a、b、c、d 这四个数成比例2、已知两个实数a,b满足条件线段求a：b的值。那么称线段AB被点P黄金分割，点P叫做线段AB的黄金分割点AP与AB的比值叫做黄金比.AP>BP已知矩形ABCD是黄金矩形，即宽与长的比是黄金比。若在矩形ABCD中
作正方形ADFE，则矩形EFCB是黄金矩形吗？此时的点E是线段AB
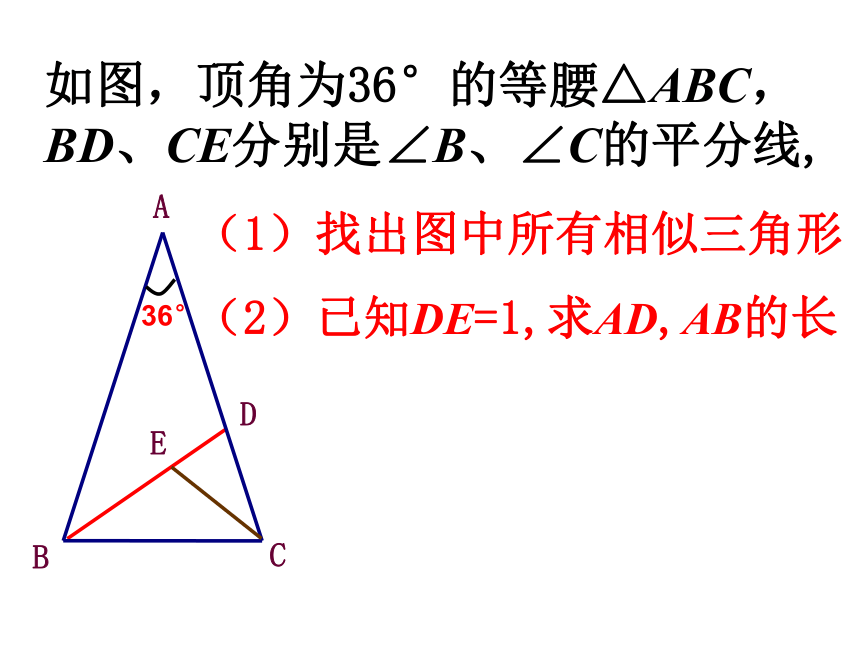
的黄金分割点吗？如果AB=12,求矩形EFCB的面积?相似三角形的判定方法：如图，顶角为36°的等腰△ABC，BD、CE分别是∠B、∠C的平分线,（2）已知DE=1,求AD,AB的长36°（1）找出图中所有相似三角形已知，DE∥BC, ∠1=∠C，找出图中所有相似的三角形找出图中相似三角形;如图，在Rt△ABC中，CD⊥AB，问：
若CD2=AD.BD,求证:∠ACB是Rt∠BC2=BD.ABAC2=AD.AB如图, 已知点P是边长为4的正方形ABCD内的一点，且PB=3，BF⊥BP。试问在射线BF上是否存在一点E，使以点B、E、C为顶点的三角形与△ABP相似?若存在,请求出BE的长;若不存在,请说明理由.FＥＥ相似图形的特例如果两个图形不仅形状相同，而且每组对应点所在的直线都经过同一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心.位似图形是相似图形的特殊情形，其相似比又叫做它们的位似比. 如图P，E，F分别是AC，AB，AD的中点，四边形AEPF与四边形ABCD是位似图形吗？如果是位似图形，说出位似中心和位似比. 位似图形的性质 位似图形上任意一对对应点到位似中心的距离之比等于位似比. 如图，已知△ABC和点O.以O为位似中心，求作△ABC的位似图形，并把△ABC的边长缩小到原来的一半. 例：如图，请以坐标原点O为位似中心，作□ ABCD的位似图形，并把它的边长放大3倍. 1．四边形GCEF与
四边形G′C′E′F′
具有怎样的对称性？
2．怎样运用像与原
像对应点的坐标关系，
画出以原点为位似中心的位似图形？以坐标原点为位似中心的位似变换有以下性质：
若原图形上点的坐标为（x，y），像与原图形的位似比为k，则像上的对应点的坐标为（kx，ky）或（―kx，―ky）. 5、如图，工人师傅为了在废旧三角形铁片上截取一个面积最大的正方形铁片，先用正方形模板在ΔABC内画一个正方形，然后过正方形在三角形内的一个顶点画射线交边AC于点G，再作GF⊥BC，F为垂足，GD∥BC交AB于D， DE⊥BC， E为垂足，则四边形DEFG就是最大的正方形，这里用到了两个正方形位似的问题，它们的位似中心是_______。