二次函数应用3（解析式）

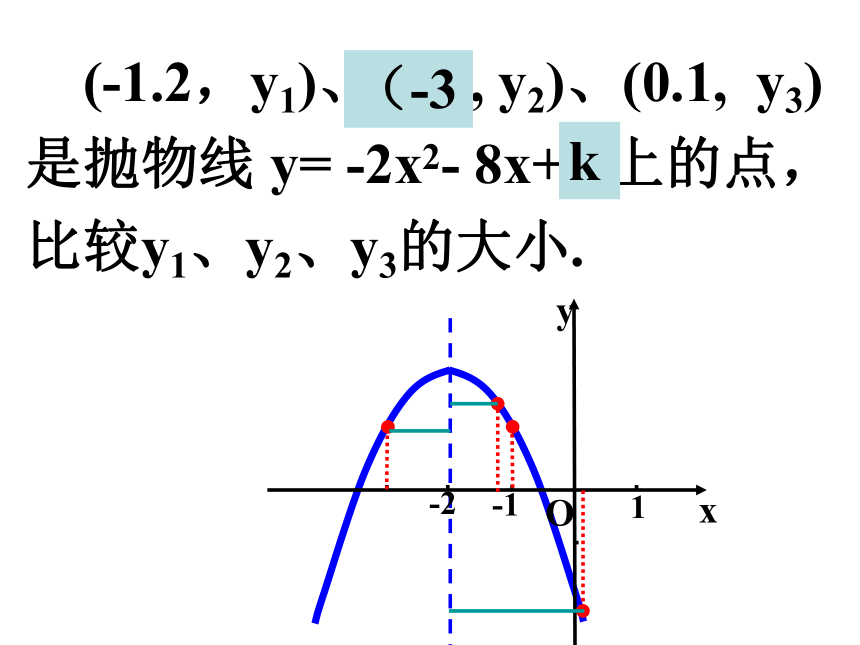
课件31张PPT。 (-1.2，y1)、(-1 , y2)、(0.1, y3)是抛物线 y= -2x2- 8x+ 3上的点， 比较y1、y2、y3的大小.k（-3作出函数 的草图 求二次函数解析式1.已知某抛物线可由
抛物线y=-3x2平移得到，且平移后经过点(0，1), (2，7),试写出该抛物线的解析式。 设y=ax2+bx+c2.已知某抛物线可由
抛物线y=-3x2平移得到，且平移后的抛物线的顶点坐标是(-2,4),试写出该抛物线的解析式。 设y=a(x+m)2+k形状相同1. 二次函数的图象过（-1,4) ,
(2, -5) , 且当x=0时，y=3.
求二次函数的解析式.2.设抛物线 过点(0, 5), 且顶
点坐标为(1,3), 求抛物线的解析式.一般式： y＝ax2＋bx＋c (a≠0)
顶点式： y＝a(x+m)2＋k (a≠0) 请说出你已经学过的二次函数解析式的表达形式：什么情况下用顶点式比较容易?1.已知二次函数的对称轴是直线 x＝1，图象上最低点P的纵坐标为-8，图象经过点(-2，10)2.某二次函数图象是y=ax2(a≠0)
的图象向左平移3个单位，再向
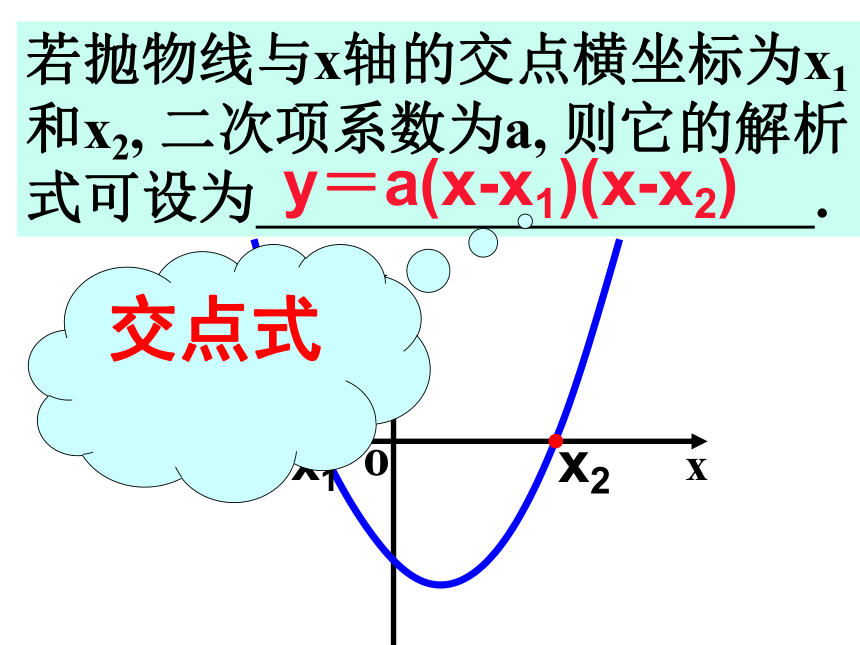
上平移2个单位得到,图象经过点(-2，3)4.当x ≥ -3时，函数值y随x的增大而增大，且当x ≤ -3时，y随x的增大而减小. 3.当x＝-3时, 函数有 最大 值2.最小(-2, 0)和(3, 0)求出下列函数与x轴的交点坐标若抛物线与x轴的交点横坐标为x1和x2, 二次项系数为a, 则它的解析式可设为 .y＝a(x-x1)(x-x2)交点式1、若已知抛物线y=ax2+bx+c与
x轴的交点横坐标为x1=2, x2=3,
且 a=1, 你能写出抛物线的解
析式吗?抛物线与y=- x2的形状、开口方向相同, 且与x轴两交点的横坐标分别为2、6. 求抛物线的解析式. 若抛物线过点(0，6)，（-1，0）（3，0）．求抛物线的解析式． 已知二次函数的图象与x轴的两交点的距离是4，且当x＝1，函数有最小值-4，求这个二次函数的解析式． 问：
1.怎么解？
2.有几种解法？如图，抛物线对称轴是x=1，与x轴交于A、B两点，若B点坐标是（ ，0），则A点的坐标为 。 设计一种方案，使这条抛物线 通过一 次平移后经过原点.两次抛物线经过三个已知点坐
标，可设二次函数的一般式:
y＝ax2＋bx＋c(a≠0) 已知抛物线的顶点坐标(或
对称轴、最值），可设顶点式:
y＝a(x+m)2＋k (a≠0) 抛物线与x轴两交点的坐标(x1,0)(x2,0),可设交点式:
y＝a(x-x1)(x-x2) (a ≠0)已知二次函数的顶点坐标是(2,1),且此函数的图象与y轴的交点坐标为（0，4），求此二次函数的解析式。求此函数图象关于 x轴 对称的
抛物线解析式；y轴原点顶点 有一个二次函数图象,三个学生
分别说出了下列一些特点:
甲: 对称轴是直线x=4
乙: 与x轴交点的横坐标都是整数
丙: 与y轴交点的纵坐标也是整数,
且以抛物线与坐标轴的交点
为顶点的三角形面积为3请你写出满足上述全部特点的
二次函数的解析式y=ax2+bx+c=要点：寻求思路时，要着重观察抛物线的开口方向，对称轴，顶点的位置，抛物线与x轴、y轴的交点的位置，注意运用数形结合的思想。6.若二次函数y=ax2 + 4x+a-1的最小值是2,则a的值是（ ）
A.4 B. -1 C. 3 D.4或-1A7.若把抛物线y=x2+bx+c向左平移2个单位,再向上平移3个单位,得抛物线y = x2 - 2x+1,则（ ）
A.b=2 B.b= - 6 , c= 6
C.b= - 8 D.b= - 8 , c= 18 B
二次函数中的符号问题 根据图象确定a、b、c、b2-4ac
的符号：y=ax2+bx+c 根据图象确定a、b、c、b2-4ac的符号：y=ax2+bx+c 根据图象确定a、b、c、b2-4ac的符号：Oxyy=ax2+bx+c 根据图象确定a、b、c、b2-4ac的符号：Oxyy=ax2+bx+c已知抛物线
的顶点在第二象限，试确定
a , b的符号-112 抛物线y=ax2+bx+c 的图象如图所示，有以下结论的是否正确①a>0
②abc<0
③b2-4ac<0
④4a+2b+c>0
⑤ a-b+c>0
⑥ 2a-3b=0,
⑦c-4b>0 已知二次函数
的图象如图所示，则函数 的图象只可能是（ ） 若一次函数 y= ax + b 的图象经过第二、三、四象限，则二次函数y = ax2 + bx - 3的大致图象是 ( )C
在同一直角坐标系中, 二次
函数y=ax2+bx+c与一次函数
y=ax+c的大致图象可能是ABCD