3.1圆(2)

课件24张PPT。圆教学目标
①学生经历不在同一直线上的三点确定一个圆的探索过程
②了解不在同一直线上的三点确定一个圆，以及过不在同一直线上的三点作圆的方法，了解并辨认三角形的外接圆、三角形的外心等概念
③会画过不在同一条直线上的三点作圆
教学重点、工具
①“不在同一直线上的三个点确定一个圆”来画图
②“不在同一直线上的三个点确定一个圆”来解决实际问题
③尺规
教学难点
对“不在同一直线上的三个点确定一个圆”中的存在性和唯一性的理解
教学方法：类比 启发
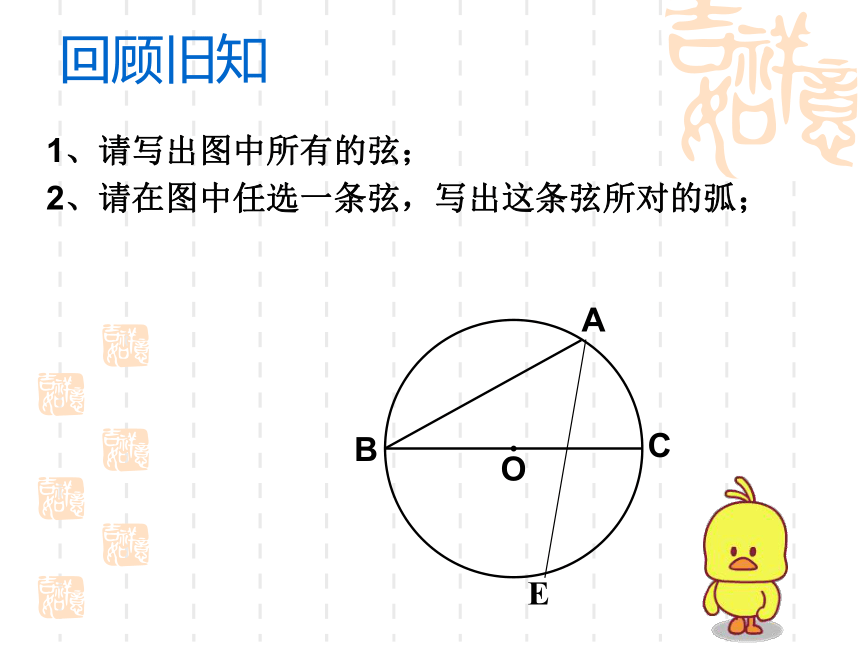
教学辅助：投影片1、请写出图中所有的弦；2、请在图中任选一条弦，写出这条弦所对的弧；回顾旧知 3、判断
（1）圆是一条封闭曲线，它上面的任何一点到某个定点的距离都等于定长。（ ）
（2）圆的任何一条弦的两端点，把圆分成两条 弧，所以一条弦对两条弧。（ ）
（3）到圆心的距离小于半径的点在圆上。（ ）
（4）直径是弦，且圆内最长的弦是直径。（ ）
（5）半圆是弧，弧小于半圆。（ ）
( 6 ) 圆上的任意两点都能将圆分成一条劣弧
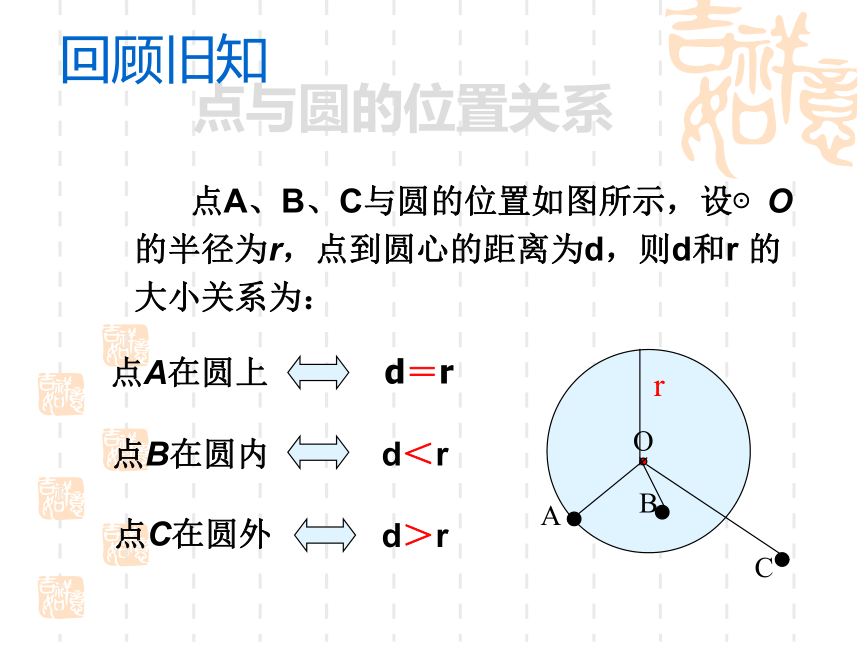
和一条优弧。（ ）√×√×√×回顾旧知 点A、B、C与圆的位置如图所示，设⊙O的半径为r，点到圆心的距离为d，则d和r 的大小关系为：d＝rd＞rd＜r点与圆的位置关系O回顾旧知问题：
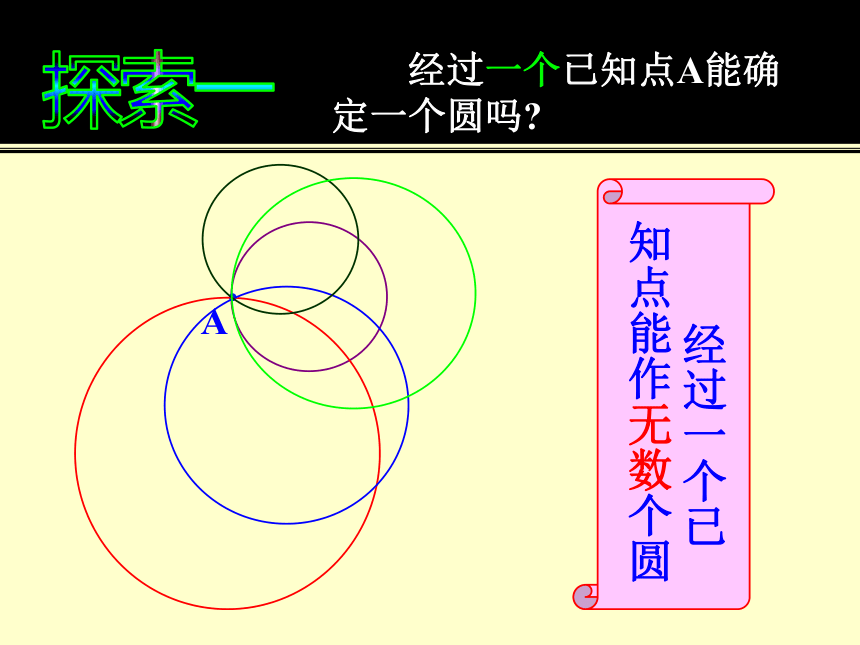
车间工人要将一个如图所示的破损的圆盘复原，你有办法吗？生活生产中的启示1、过一点可以作几条直线？2、过几点可确定一条直线？ 过几点可以确定一个圆呢？知识回顾探索一 经过一个已知点A能确定一个圆吗?A 经过一个已知点能作无数个圆
探索二 经过两个已知点A、B能确定一个圆吗?AB 经过两个已知点A、B能作无数个圆 经过两个已知点A、B所作的圆的圆心在怎样的一条直线上?
探索三 经过三个已知点A，B，C能确定一个圆吗？假设经过A、B、C三点的⊙O存在（1）圆心O到A、B、C三点距离 （填“相等”或”不相等”）。（2）连结AB、AC，过O点 分别作直线MN⊥AB， EF⊥AC，则MN是AB的 ；EF是AC的 。（3）AB、AC的中垂线的交点O到B、C的距离 。NMFE相等垂直平分线垂直平分线相等ABC过如下三点能不能做圆? 为什么?讨论不在同一直线上的三点确定一个圆做一做:平面上有4个点,它们不在一条直线上,但有3个点在同一条直线上.问过其中3个点作圆,可以作出几个圆?画一画已知：不在同一直线上的三点A、B、C
求作： ⊙O使它经过点A、B、C作法：1、连结AB，作线段AB的垂直平分线MN；
2、连接AC，作线段AC的垂直平分线EF，交MN于点O；
3、以O为圆心，OB为半径作圆。
所以⊙O就是所求作的圆。ONMFEABC 现在你知道了怎样要将一个如图所示的破损的圆盘复原了吗？方法:
寻求圆弧所在圆的圆心,
在圆弧上任取三点,作其
连线段的垂直平分线,其
交点即为圆心.练一练 已知△ABC，用直尺和圆规作出过点A、B、C的圆O定义 经过三角形各个顶点的圆 叫做三角形的外接圆，外接圆 的圆心叫做三角形的外心，这个三角形叫做圆的内接三角形。如图：⊙O是△ABC的外接圆， △ABC是⊙O的内接三角形，点O是△ABC的外心外心是△ABC三条边的垂直平分线的交点找一找 如图，请找出图中圆的圆心，并写出你找圆心的方法?ABCO试一试画出过以下三角形的顶点的圆●OCAB┐●O●O思 考1、比较这三个三角形外心的位置，你有何发现？2、图二中，若AB=3，BC=4，则它的外接圆半径是多少？（图一）（图二）（图三）直角三角形的外心是斜边的中点.直角三角形斜边就是外接圆的一条直径.做一做:(1)已知直角三角形的两条直角边长是6cm和8cm,则这个三角形的外接圆的半径是______cm.5圆上(2)如图, ∠ABC=∠ADC=900.若△ABC的外接圆为⊙O,则点D与⊙O的位置是:点在______.练一练1.下列命题不正确的是
A.过一点有无数个圆. B.过两点有无数个圆.
C.弦是圆的一部分. D.过同一直线上三点不能画圆.
2.三角形的外心具有的性质是
A.到三边的距离相等. B.到三个顶点的距离相等.
C.外心在三角形的外. D.外心在三角形内.CB⊙某市要建一个圆形公园，要求公园刚好把动物园A，植物园B和人工湖C包括在内，又要使这个圆形的面积最小，请你给出这个公园的施工图。（A、B、C不在同一直线上）探究活动植物园动物园人工湖图中工具的CD边所在直线恰好垂直平分AB边，怎样用这个工具找出一个圆的圆心。数学乐园谈收获:（1）只有确定了圆心和圆的半径，这个圆的位置和大小才唯一确定。（2）经过一个已知点能作无数个圆！（3）经过两个已知点A、B能作无数个圆！这些圆的圆心在线段AB的垂直平分线上。（4）不在同一直线上的三个点确定一个圆。（5）外接圆，外心的概念。