3.3圆心角(1)
图片预览





文档简介
课件40张PPT。直径CD⊥AB圆的轴对称性
垂径定理及逆定理复习回顾3.3 圆心角(1)义务教育课程标准实验教科
浙江版《数学》九年级上册
茶杯的盖子做成圆
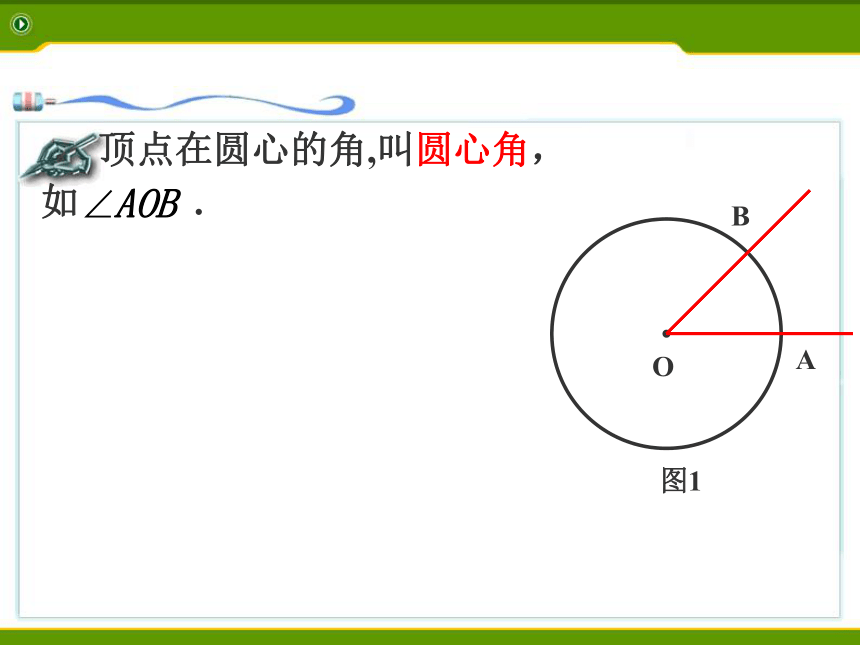
形有什么好处呢? 圆绕圆心旋转任意一个角度,都能够与原来的圆重合。圆的旋转不变性:圆是中心对称图形,圆心是它的对称中心。AB 顶点在圆心的角,叫圆心角,
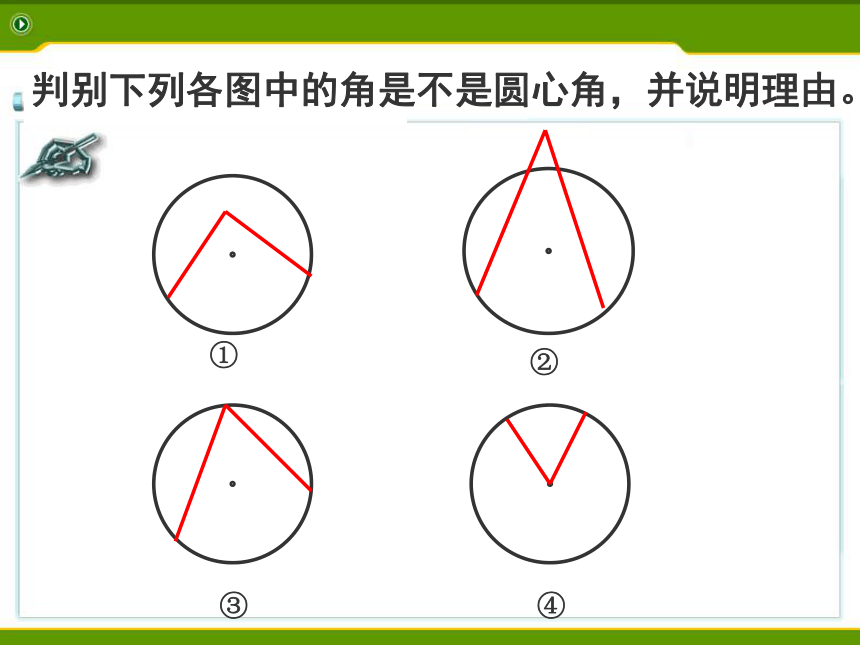
如 . 图1 判别下列各图中的角是不是圆心角,并说明理由。①②③④ 过点O作弦AB的垂线, 垂足
为M,AB 顶点在圆心的角,叫圆心角,
如 , 所对的弦为AB;图1 则垂线段OM的长度,即圆
心到弦的距离,叫弦心距 , 图1
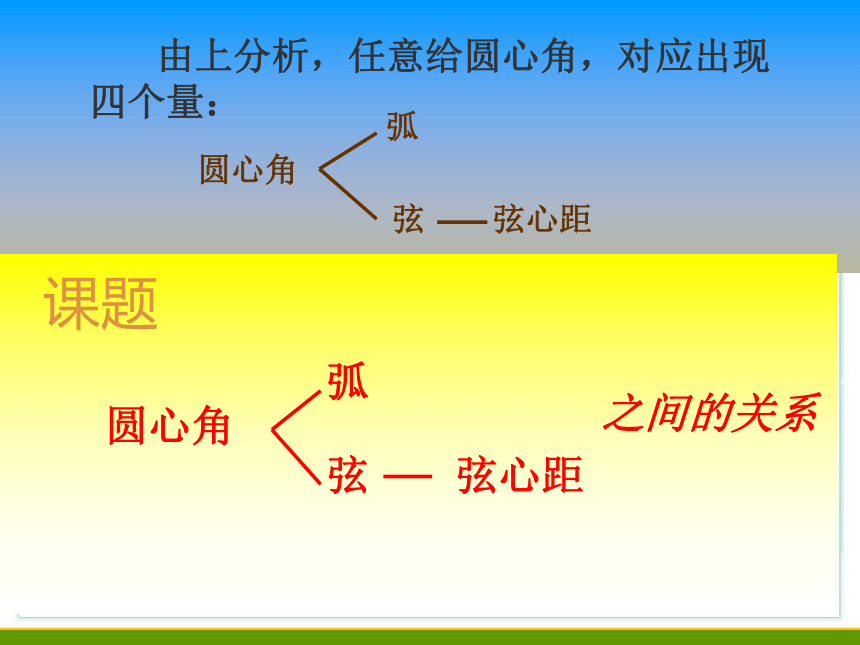
中,OM为AB弦的弦心距。OM是唯一的。 由上分析,任意给圆心角,对应出现
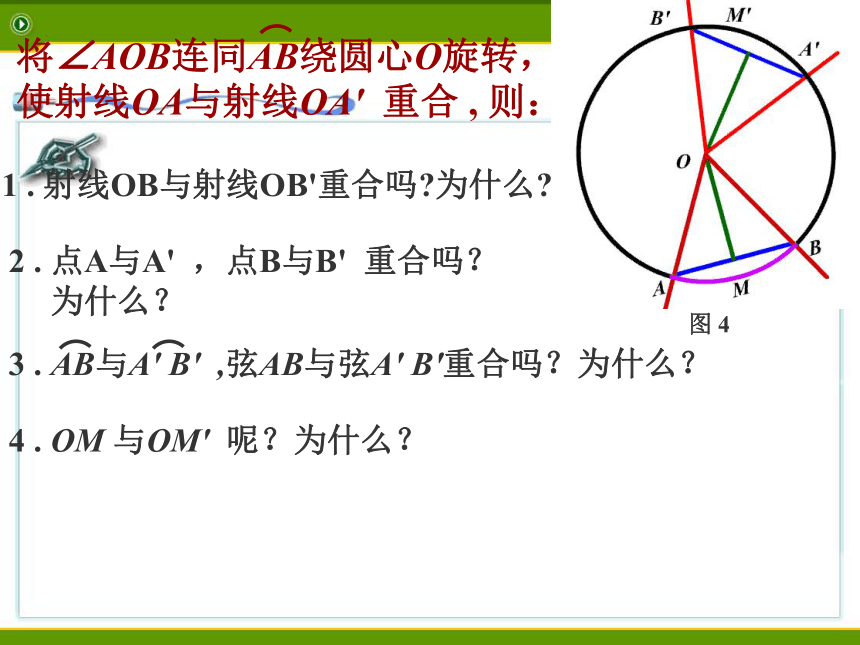
四个量:圆心角弧弦 弦心距1 . 射线OB与射线OB'重合吗?为什么?2 . 点A与A' ,点B与B' 重合吗?
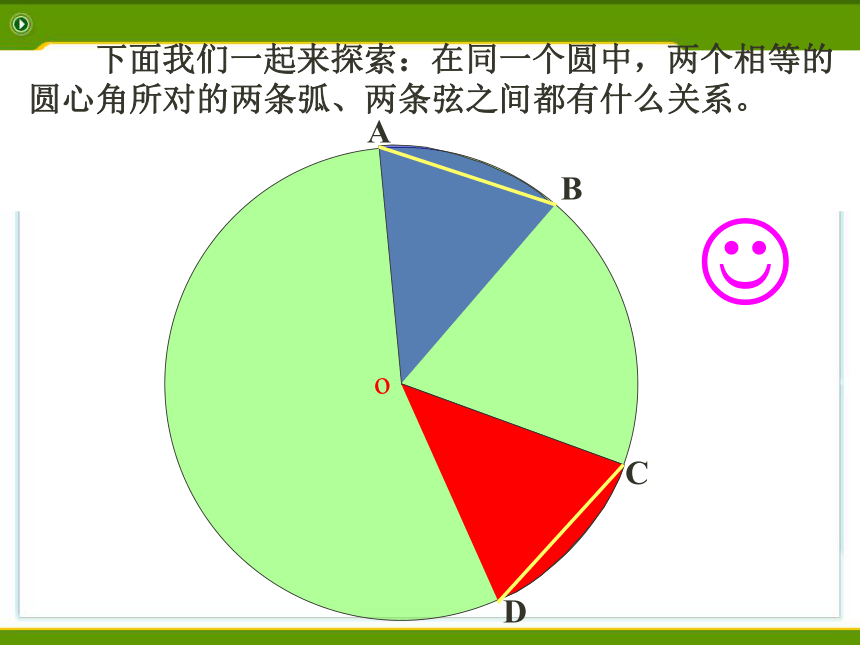
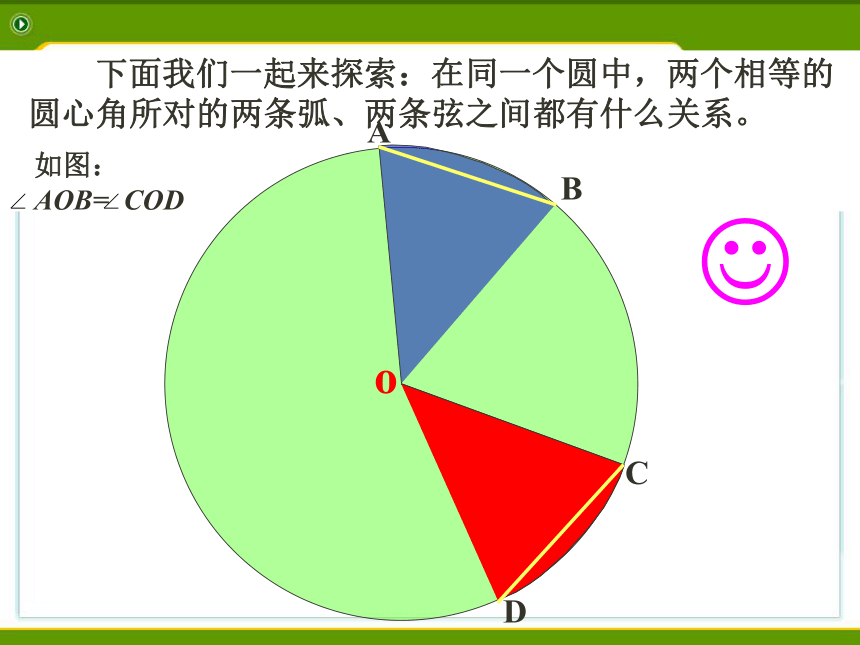
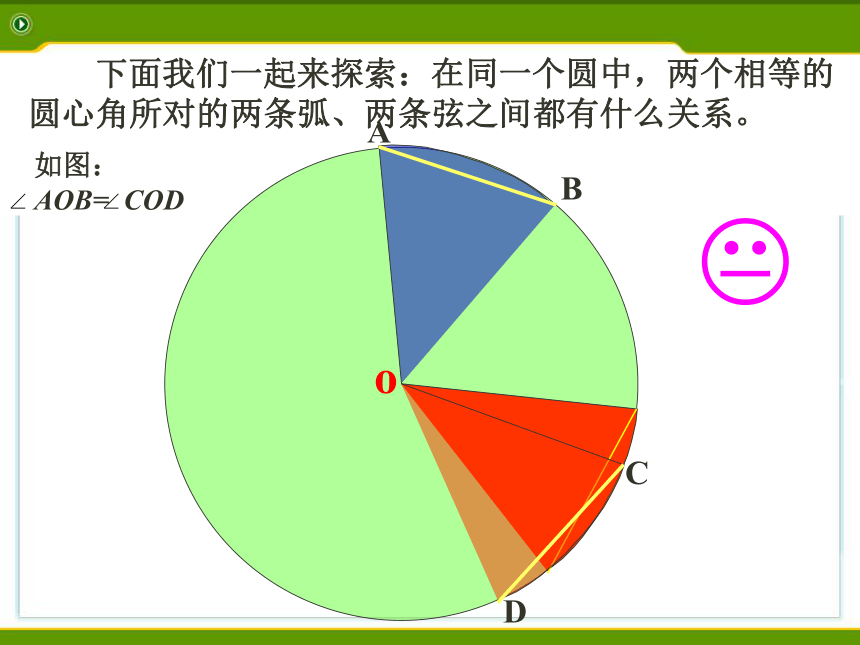
为什么?4 . OM 与OM' 呢?为什么?图 4 CDo?AB 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。CDo?AB 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。圆心角定理: 弦AB和弦CD对应的弦心距什么关系?相等的圆心角所对的弧相等,
所对的弦相等 所对弦的弦心距相等在同圆或等圆中,∵ ∠ AOB= ∠ CODABCDAB=CD吗?弧AB与弧CD呢?O圆心角定理: 相等的圆心角所对的弧相等,
所对的弦相等 所对弦的弦心距相等在同圆中,如图,⊙O 和⊙O' 是等圆,
如果 ∠AOB= ∠ A'O'B'
那么 AB=A'B' 、AB= A'B' 、OM=O'M',
为什么???? 对于等圆的情况 ,因为两个等圆可
叠合成同圆,所以等圆问题可转化为同圆问题,
命题成立。条件结论在同圆或等圆中
如果圆心角相等那么相等圆心角所对的弧相等相等圆心角所对的弦相等相等圆心角所对的弦的
弦心距相等1.相等的圆心角所对的弧相等。( )2.已知:如图, ∠ 1= ∠ 2,求证:AC=BD证明:∵ ∠ 1= ∠ 2练一练(1):O例1:用直尺和圆规把⊙O四等分. O 作法:1、作⊙O的直径AB。
2、过点O作CD⊥AB,交⊙O于
点C和点D。
点A,B,C,D就把⊙O四等分
六例1:用直尺和圆规把⊙O四等分. O 作法:1、作⊙O的直径AB。
2、过点O作CD⊥AB,交⊙O于
点C和点D。
点A,B,C,D就把⊙O四等分
我们把1o的圆心角所对的弧叫做1o的弧.这样,1o的圆心角对着1o的弧,
1o的弧对着1o的圆心角.
n o的圆心角对着no的弧,
n o的弧对着no的圆心角. 性质:弧的度数和它所对圆心角的度数相等.AOB练一练(2):1.如图一,已知∠AOC=135°,
则CB的度数为—— 45°图(一)2.如图,∵∠AOC=∠BOD
∴AC =BD
问:以上说法对不对?为什么?那么,怎样情况下, AC =BD?P70:课内练习33.下列说法正确的是( )
A.相等的圆心角所对的弧相等。
B.相等的圆心角所对的弦相等。
C.度数相等的两条弧相等。
D.相等的圆心角所对的弧的度数相等。
D ABCDO做一做:巩固练习:5.如图: ⊙O的直径AB垂直于弦CD,AB与CD相交于点E,
∠ COD=1000,求BC,AD的度数ABCDOE解:∵OC=OD,OE⊥CD
∴∠1= ∠212∵∠COD=1000∴∠1=∠2=500如图,C是圆0的直径AB上一点,过点C做弦DE,使CD=CO,若 AD的度数为40,求BE的度数。。ABCDOE拓展练习通过本节的学习,你对圆有哪些新的认识?回顾与小结探究活动如何只用圆规把一个圆四等分?
垂径定理及逆定理复习回顾3.3 圆心角(1)义务教育课程标准实验教科
浙江版《数学》九年级上册
茶杯的盖子做成圆
形有什么好处呢? 圆绕圆心旋转任意一个角度,都能够与原来的圆重合。圆的旋转不变性:圆是中心对称图形,圆心是它的对称中心。AB 顶点在圆心的角,叫圆心角,
如 . 图1 判别下列各图中的角是不是圆心角,并说明理由。①②③④ 过点O作弦AB的垂线, 垂足
为M,AB 顶点在圆心的角,叫圆心角,
如 , 所对的弦为AB;图1 则垂线段OM的长度,即圆
心到弦的距离,叫弦心距 , 图1
中,OM为AB弦的弦心距。OM是唯一的。 由上分析,任意给圆心角,对应出现
四个量:圆心角弧弦 弦心距1 . 射线OB与射线OB'重合吗?为什么?2 . 点A与A' ,点B与B' 重合吗?
为什么?4 . OM 与OM' 呢?为什么?图 4 CDo?AB 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。CDo?AB 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。o?ABCD 下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。圆心角定理: 弦AB和弦CD对应的弦心距什么关系?相等的圆心角所对的弧相等,
所对的弦相等 所对弦的弦心距相等在同圆或等圆中,∵ ∠ AOB= ∠ CODABCDAB=CD吗?弧AB与弧CD呢?O圆心角定理: 相等的圆心角所对的弧相等,
所对的弦相等 所对弦的弦心距相等在同圆中,如图,⊙O 和⊙O' 是等圆,
如果 ∠AOB= ∠ A'O'B'
那么 AB=A'B' 、AB= A'B' 、OM=O'M',
为什么???? 对于等圆的情况 ,因为两个等圆可
叠合成同圆,所以等圆问题可转化为同圆问题,
命题成立。条件结论在同圆或等圆中
如果圆心角相等那么相等圆心角所对的弧相等相等圆心角所对的弦相等相等圆心角所对的弦的
弦心距相等1.相等的圆心角所对的弧相等。( )2.已知:如图, ∠ 1= ∠ 2,求证:AC=BD证明:∵ ∠ 1= ∠ 2练一练(1):O例1:用直尺和圆规把⊙O四等分. O 作法:1、作⊙O的直径AB。
2、过点O作CD⊥AB,交⊙O于
点C和点D。
点A,B,C,D就把⊙O四等分
六例1:用直尺和圆规把⊙O四等分. O 作法:1、作⊙O的直径AB。
2、过点O作CD⊥AB,交⊙O于
点C和点D。
点A,B,C,D就把⊙O四等分
我们把1o的圆心角所对的弧叫做1o的弧.这样,1o的圆心角对着1o的弧,
1o的弧对着1o的圆心角.
n o的圆心角对着no的弧,
n o的弧对着no的圆心角. 性质:弧的度数和它所对圆心角的度数相等.AOB练一练(2):1.如图一,已知∠AOC=135°,
则CB的度数为—— 45°图(一)2.如图,∵∠AOC=∠BOD
∴AC =BD
问:以上说法对不对?为什么?那么,怎样情况下, AC =BD?P70:课内练习33.下列说法正确的是( )
A.相等的圆心角所对的弧相等。
B.相等的圆心角所对的弦相等。
C.度数相等的两条弧相等。
D.相等的圆心角所对的弧的度数相等。
D ABCDO做一做:巩固练习:5.如图: ⊙O的直径AB垂直于弦CD,AB与CD相交于点E,
∠ COD=1000,求BC,AD的度数ABCDOE解:∵OC=OD,OE⊥CD
∴∠1= ∠212∵∠COD=1000∴∠1=∠2=500如图,C是圆0的直径AB上一点,过点C做弦DE,使CD=CO,若 AD的度数为40,求BE的度数。。ABCDOE拓展练习通过本节的学习,你对圆有哪些新的认识?回顾与小结探究活动如何只用圆规把一个圆四等分?
同课章节目录
