2.6探索勾股定理

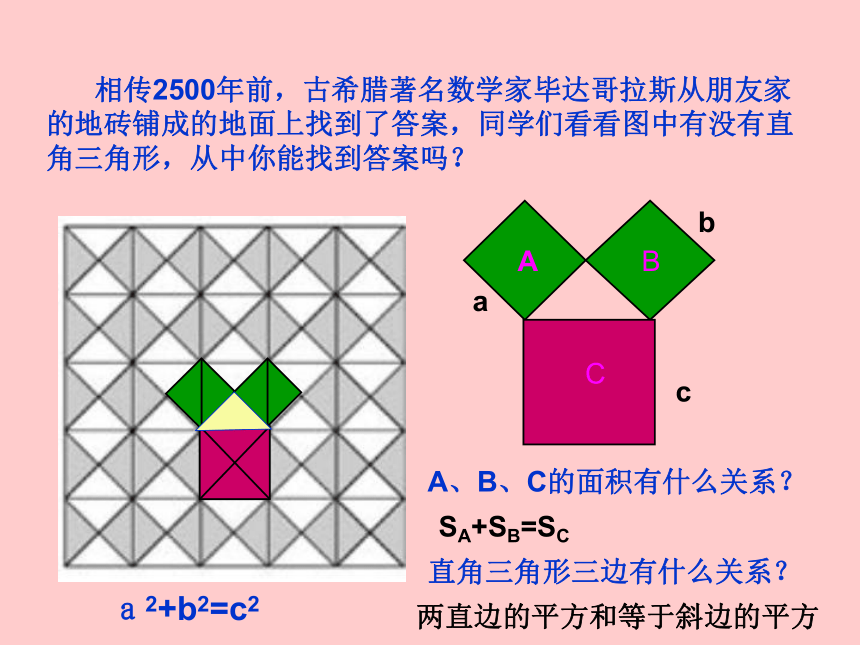
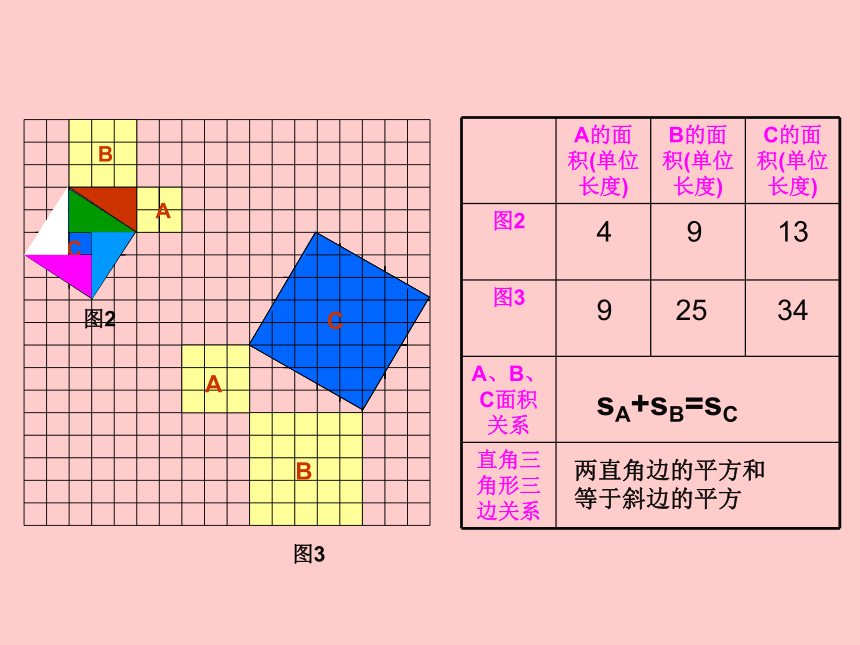
课件15张PPT。18.1 勾股定理abc　　 相传2500年前，古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了答案，同学们看看图中有没有直角三角形，从中你能找到答案吗？A、B、C的面积有什么关系？直角三角形三边有什么关系？SA+SB=SC两直边的平方和等于斜边的平方ａ2+b2=c2abcABC图2图3491392534sA+sB=sC两直角边的平方和
等于斜边的平方命题１：如果直角三角形的两直角边长分别为a、b，斜边长为c，那么a2+b2=c2。abc你能证明这个命题是正确的命题吗？赵爽的证法插入动画演示毕达哥拉斯证法:abcaabbc ?(a + b)(b + a) = ?c2 + 2(?ab)
?a2 + ab + ?b2 = ?c2 + ab
? a2 + b2 = c2aabbcc伽菲尔德经过反复的思考与演算，终于弄清楚了其中的道理，并给出了简洁的证明方法．1876年4月1日，伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。1881年，伽菲尔德就任美国第二十任总统后，人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明，就称这一证法称为“总统”证法。
∟∟∟abcabc2、s大正方形=(a+b)2=a2+2ab+b2
s大正方形=c2+4× ab=c2+2ab
∵s大正方形=s大正方形
∴a2+2ab+b2=c2+2ab
∴a2+b2=c2
3、s大正方形=c2
s大正方形=4× ab+(b-a)2
=2ab+b2-2ab+b2
=a2+b2
∵s大正方形=s大正方形
∴c2=a2+b2 　　定理：经过证明被确认为正确的命题叫做定理。　勾股定理：如果直角三角形的两直角边长分别为ａ、ｂ，斜边为ｃ，那么a2+b2=c2。练习：
1、求下列图中字母所表示的正方形的面积=625=1442、求出下列直角三角形中未知边的长度解：由勾股定理得：x2 =36+64x2 =100x2=62+82∴ x=10∵ x2+52=132∴ x2=132-52x2 =169-25x2 =144∴ x=12∵ x > 0∵ x > 01、放学以后，小红和小颖从学校分手，分别沿着东方向和南方向回家，若小红和小颖行走的速度都是40米/分，小红用15分钟到家，小颖用20分钟到家，小红和小颖家的距离为 （ ）
A、600米 B、800米
C、1000米 D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米，那么斜边上的高是 （ ）
A、6厘米 B、 8厘米
C、 80/13厘米； D、 60/13厘米； CD１、本节课我们经历了怎样的过程？　　经历了从实际问题引入数学问题然后发现定理，再到探
索定理，最后学会验证定理及应用定理解决实际问题的过程。　２、本节课我们学到了什么？　　通过本节课的学习我们不但知道了著名的勾股定理，还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。３、学了本节课后我们有什么感想？　　 很多的数学结论存在于平常的生活中，需要我们用数学
的眼光去观察、思考、发现，这节课我们还受到了数学文化
辉煌历史的教育。