3.4 圆周角
图片预览



文档简介
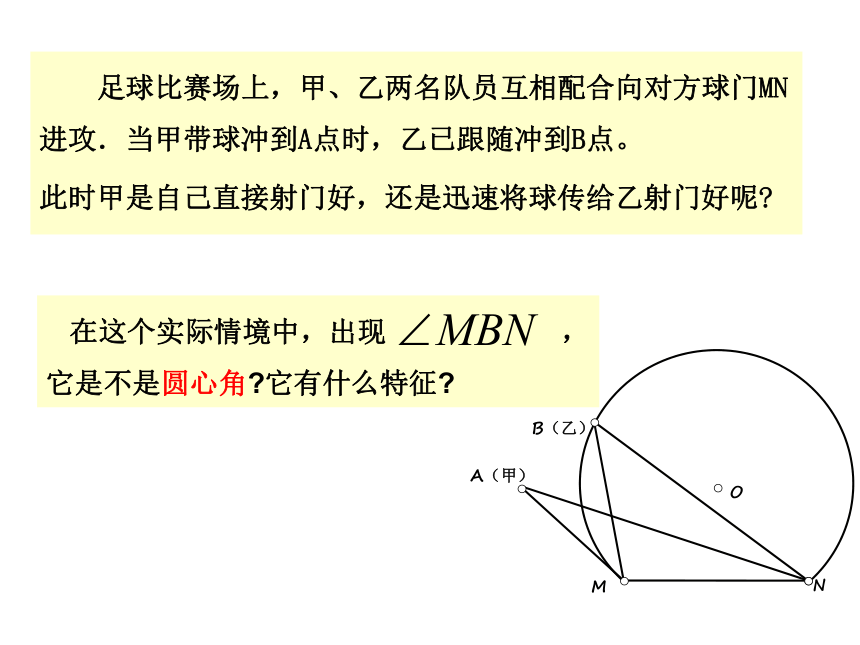
课件32张PPT。老师、同学们上午好! 足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻.当甲带球冲到A点时,乙已跟随冲到B点。
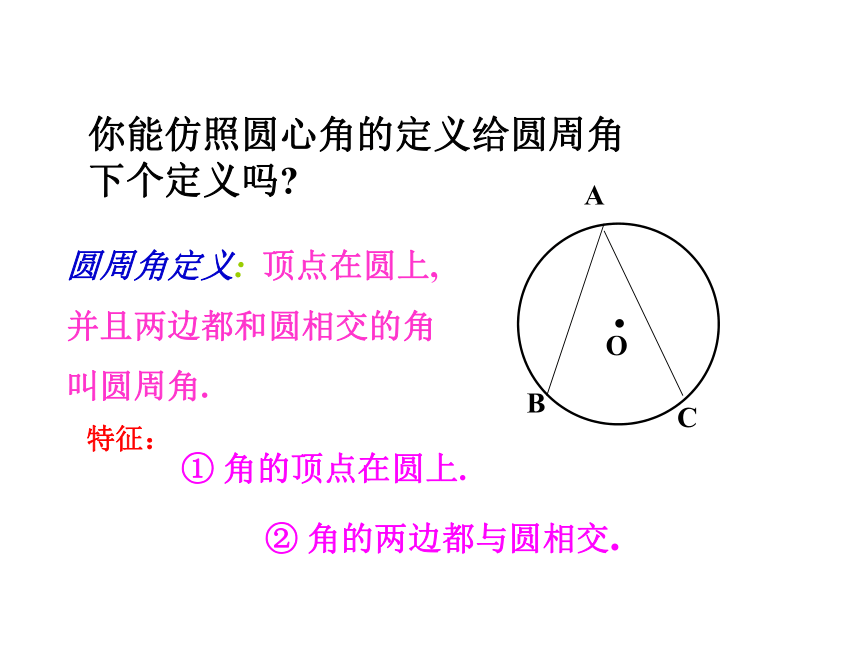
此时甲是自己直接射门好,还是迅速将球传给乙射门好呢? MNA(甲)OB(乙)你能仿照圆心角的定义给圆周角 下个定义吗?特征:① 角的顶点在圆上.② 角的两边都与圆相交.圆周角定义: 顶点在圆上,
并且两边都和圆相交的角
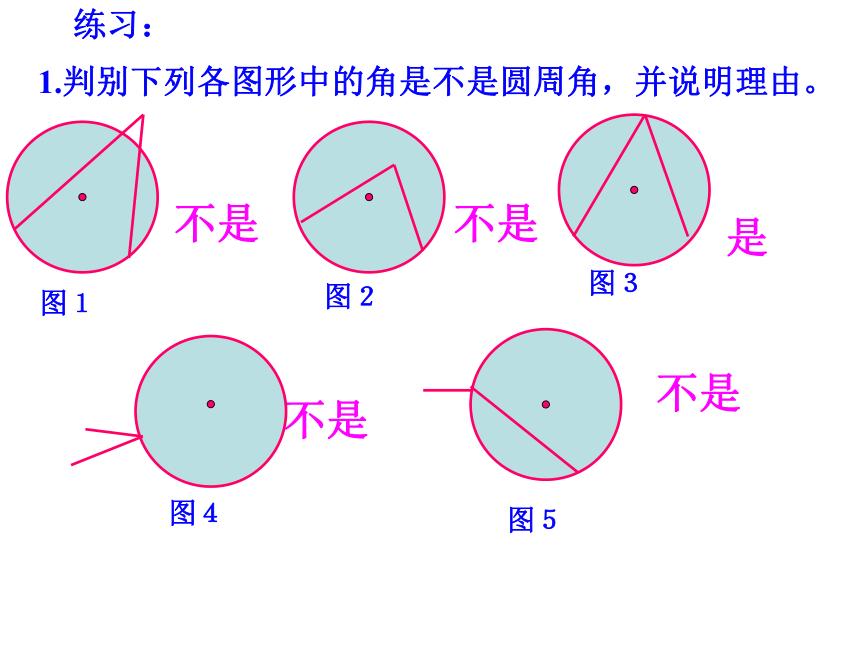
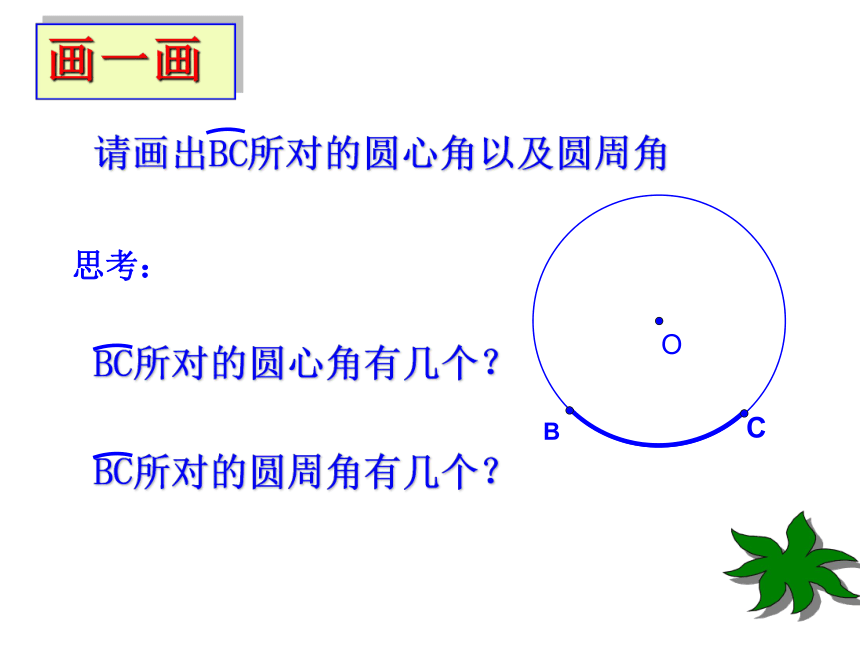
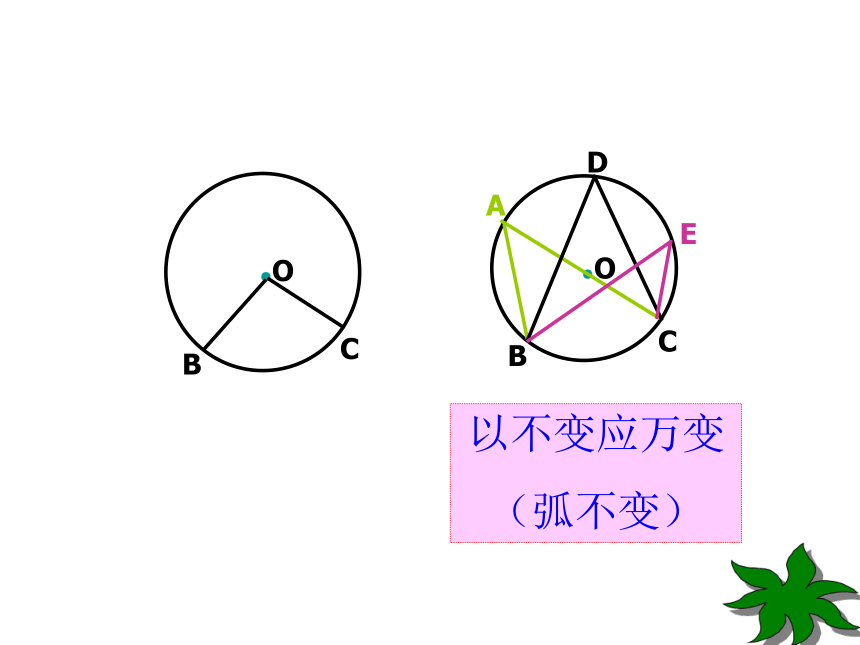
叫圆周角.练习:1.判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是图1图2图3图4图5请画出BC所对的圆心角以及圆周角画一画思考:BC以不变应万变
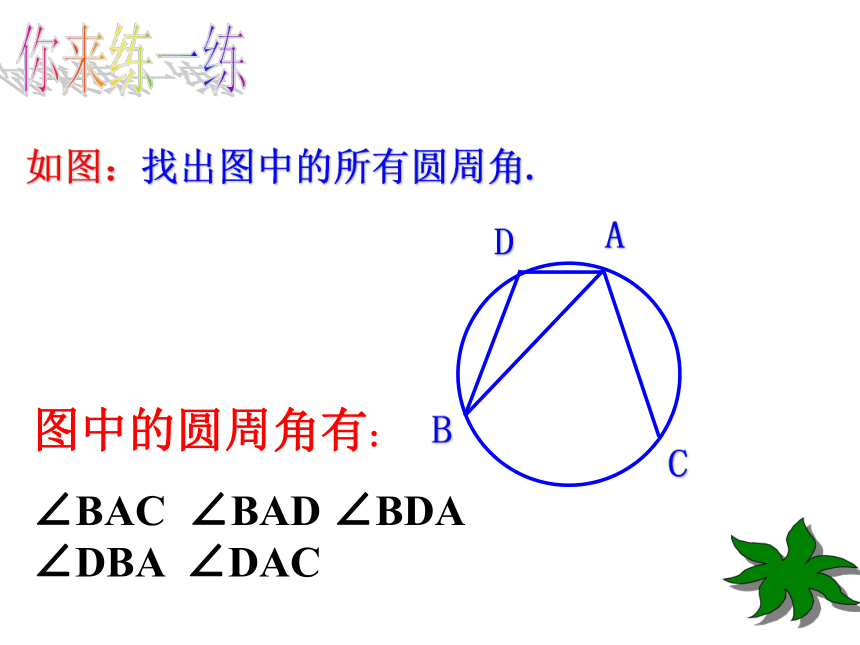
(弧不变)如图:找出图中的所有圆周角.你来练一练图中的圆周角有:
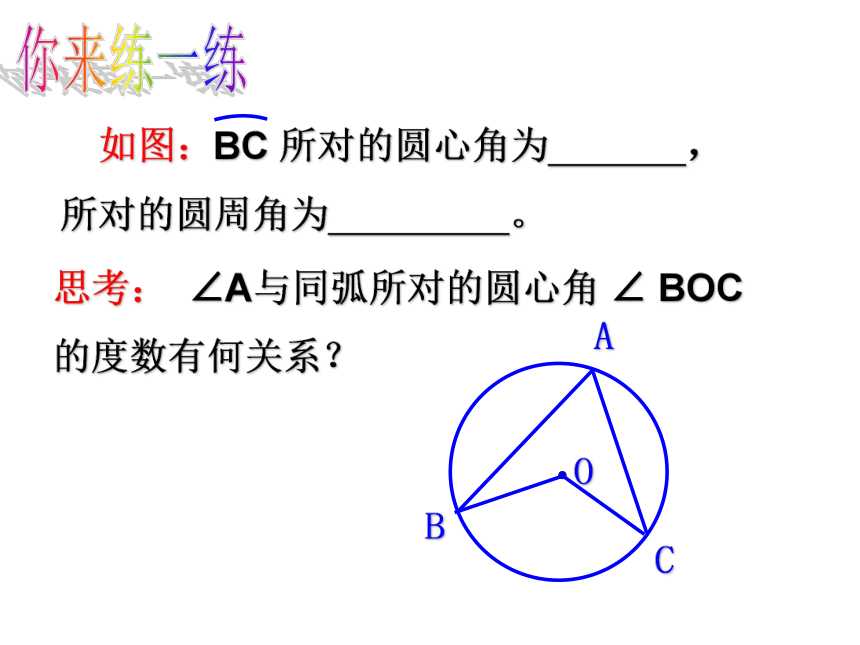
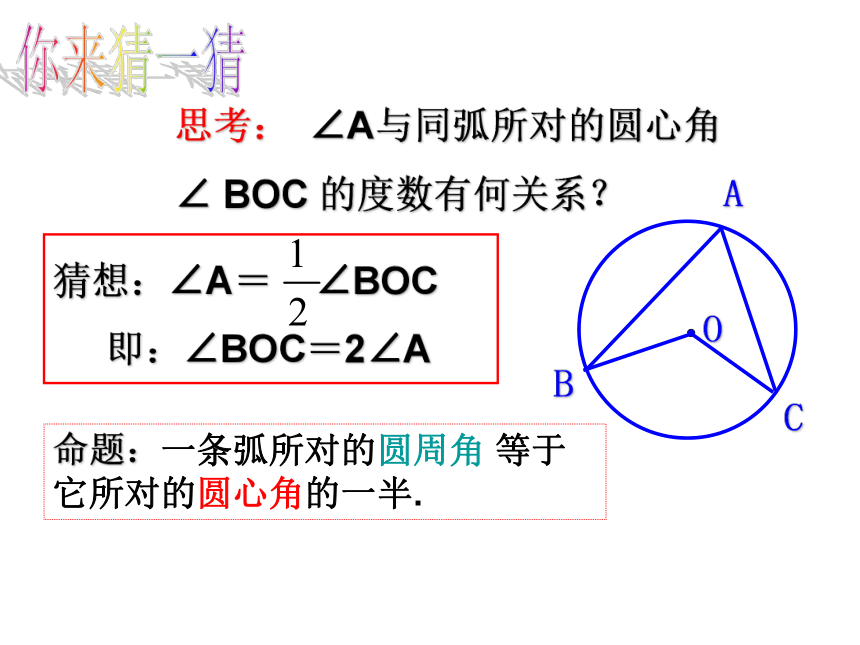
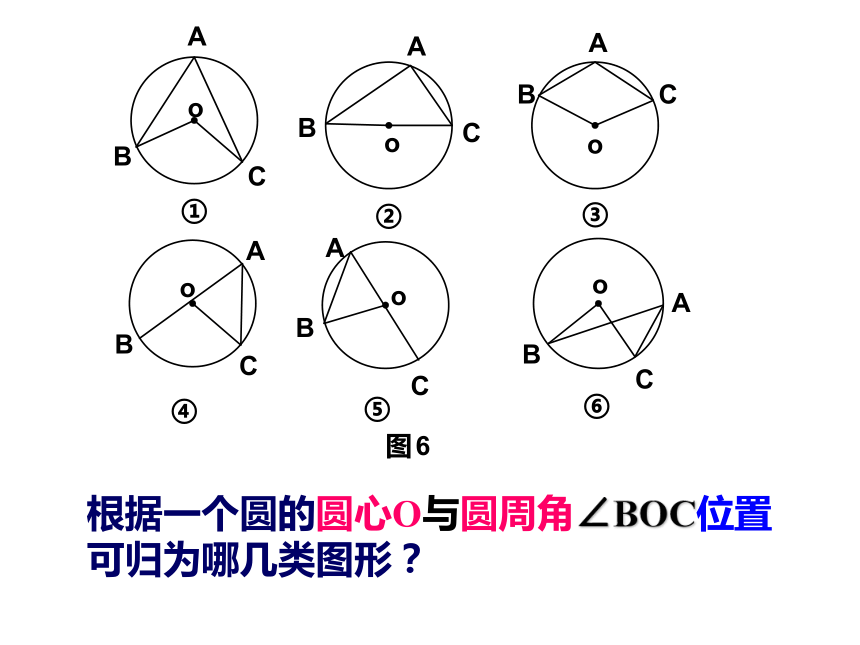
∠BAC ∠BAD ∠BDA ∠DBA ∠DAC 你来练一练思考: ∠A与同弧所对的圆心角 ∠ BOC 的度数有何关系?你来猜一猜思考: ∠A与同弧所对的圆心角 ∠ BOC 的度数有何关系?命题:一条弧所对的圆周角 等于它所对的圆心角的一半.命题证明三部曲:作图——已知条件——证明根据一个圆的圆心O与圆周角∠BOC位置可归为哪几类图形?ABCOABCCOOAB温馨提示:归类...DD 角边上 角内 角外 在这三个图中,哪个图形最特殊?其余两个可以转化成这个图形吗?CABCCOOAB温馨提示:归类 角边上 角内 角外C特殊:圆心O落在圆周角的边上!! BACDO能否也使圆心O落在圆周角的边上? BACDO能否也使圆心O落在圆周角的边上? 圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半。1、100o的弧所对的圆心角等于_____,所对的圆周角等于_____。
2如图,在⊙O中,∠BAC=32o,则∠BOC=________。
3、如图,⊙O中,∠ACB = 130o,则∠AOB=______。
4、下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角。
(B)60o的圆周角所对的弧的度数是30o
(C)一弧所对的圆周角等于它所对的圆心角。
(D)80o的弧所对的圆周角是40o100o50o64o100oD学以致用5.求圆中角X的度数 D B学以致用问题1: 弧所对的圆心角是 度, 所对的圆周角是 度。造句子:
说明一条弧的度数、一条弧所对的圆心角的度数、一条弧所对的圆周角的度数三者之间的数量关系!学以致用一条弧的度数=一条弧所对的圆心角的度数
=一条弧所对的圆周角的度数x2∠C =∠D=∠E七嘴八舌同弧所对的圆周角相等! 问题2、如图2,AB是⊙O的直径,C是⊙O上任一点,你能确定∠BAC的度数吗?∠BAC=90o问题3:如图3,圆周角∠BAC=90o,弦BC经过圆心O吗?为什么?半圆或直径所对的圆周角是直角,
90°的圆周角的所对的弦是直径。推论:试一试只给你一把三角尺,你能找出一个圆(如图)的圆心吗?例1:已知:如图,四边形ABCD的四个顶点在⊙O上,求证:∠B+∠D=1800例题欣赏变式1:已知:如图,四边形ABCD的四个顶点在⊙O上,∠A=100°,点E在BC的延长线上,求∠DCE的度数。 足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻.当甲带球冲到A点时,乙已跟随冲到B点。
此时甲是自己直接射门好,还是迅速将球传给乙射门好呢? MNA(甲)OB(乙)射门优势取决于入射角度,角度越大越好!C回头看看书山有路勤为径,学海无涯苦作舟。本节课你学到了什么? 有何收获? 本节课涉及:
(1)研究方法:特殊 —— 一般 —— 特殊
(2)数学思想:转化、分类讨论。猜想归纳应用1、圆周角的概念。
2、圆周角的定理及推论。
3、应用定理及推论。 本节课你体会到了哪些数学思想与方法? 同学们再见!作业:
1、作业本3.4(1)
2、课时训练—基础题OCBAD例题欣赏变式3:如图,在⊙O中,∠AOC=1200,∠ACB=250,求∠BAC的度数。想一想如图,在△ABC中,以BC边为直径画圆,分别交AB,AC于点D,E,连结BE,CD.已知BE=CD,
求证:△ABC是等腰三角形.
此时甲是自己直接射门好,还是迅速将球传给乙射门好呢? MNA(甲)OB(乙)你能仿照圆心角的定义给圆周角 下个定义吗?特征:① 角的顶点在圆上.② 角的两边都与圆相交.圆周角定义: 顶点在圆上,
并且两边都和圆相交的角
叫圆周角.练习:1.判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是图1图2图3图4图5请画出BC所对的圆心角以及圆周角画一画思考:BC以不变应万变
(弧不变)如图:找出图中的所有圆周角.你来练一练图中的圆周角有:
∠BAC ∠BAD ∠BDA ∠DBA ∠DAC 你来练一练思考: ∠A与同弧所对的圆心角 ∠ BOC 的度数有何关系?你来猜一猜思考: ∠A与同弧所对的圆心角 ∠ BOC 的度数有何关系?命题:一条弧所对的圆周角 等于它所对的圆心角的一半.命题证明三部曲:作图——已知条件——证明根据一个圆的圆心O与圆周角∠BOC位置可归为哪几类图形?ABCOABCCOOAB温馨提示:归类...DD 角边上 角内 角外 在这三个图中,哪个图形最特殊?其余两个可以转化成这个图形吗?CABCCOOAB温馨提示:归类 角边上 角内 角外C特殊:圆心O落在圆周角的边上!! BACDO能否也使圆心O落在圆周角的边上? BACDO能否也使圆心O落在圆周角的边上? 圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半。1、100o的弧所对的圆心角等于_____,所对的圆周角等于_____。
2如图,在⊙O中,∠BAC=32o,则∠BOC=________。
3、如图,⊙O中,∠ACB = 130o,则∠AOB=______。
4、下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角。
(B)60o的圆周角所对的弧的度数是30o
(C)一弧所对的圆周角等于它所对的圆心角。
(D)80o的弧所对的圆周角是40o100o50o64o100oD学以致用5.求圆中角X的度数 D B学以致用问题1: 弧所对的圆心角是 度, 所对的圆周角是 度。造句子:
说明一条弧的度数、一条弧所对的圆心角的度数、一条弧所对的圆周角的度数三者之间的数量关系!学以致用一条弧的度数=一条弧所对的圆心角的度数
=一条弧所对的圆周角的度数x2∠C =∠D=∠E七嘴八舌同弧所对的圆周角相等! 问题2、如图2,AB是⊙O的直径,C是⊙O上任一点,你能确定∠BAC的度数吗?∠BAC=90o问题3:如图3,圆周角∠BAC=90o,弦BC经过圆心O吗?为什么?半圆或直径所对的圆周角是直角,
90°的圆周角的所对的弦是直径。推论:试一试只给你一把三角尺,你能找出一个圆(如图)的圆心吗?例1:已知:如图,四边形ABCD的四个顶点在⊙O上,求证:∠B+∠D=1800例题欣赏变式1:已知:如图,四边形ABCD的四个顶点在⊙O上,∠A=100°,点E在BC的延长线上,求∠DCE的度数。 足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻.当甲带球冲到A点时,乙已跟随冲到B点。
此时甲是自己直接射门好,还是迅速将球传给乙射门好呢? MNA(甲)OB(乙)射门优势取决于入射角度,角度越大越好!C回头看看书山有路勤为径,学海无涯苦作舟。本节课你学到了什么? 有何收获? 本节课涉及:
(1)研究方法:特殊 —— 一般 —— 特殊
(2)数学思想:转化、分类讨论。猜想归纳应用1、圆周角的概念。
2、圆周角的定理及推论。
3、应用定理及推论。 本节课你体会到了哪些数学思想与方法? 同学们再见!作业:
1、作业本3.4(1)
2、课时训练—基础题OCBAD例题欣赏变式3:如图,在⊙O中,∠AOC=1200,∠ACB=250,求∠BAC的度数。想一想如图,在△ABC中,以BC边为直径画圆,分别交AB,AC于点D,E,连结BE,CD.已知BE=CD,
求证:△ABC是等腰三角形.
同课章节目录
