1.4绝对值

课件21张PPT。1.4 绝对值数轴的三要素:原点、单位长度 、正方向复习回顾相反数:如果两个数只有符号不同,就称其中一个数为
另一个数的相反数，也称这两个数互为相反数.在数轴上,表示互为相反数的两个数(零除外)的两个点,位于原点两侧,并且到原点的距离相等.注意：零的相反数是零.2.在数轴上,点C表示有理数+2,到点C距离为3个单位的点表示的有理数有几个?是谁?1.问在A、B之间的整数有几个？负整数有几个?甲、乙两辆车在一条东西走向的街道上行驶,
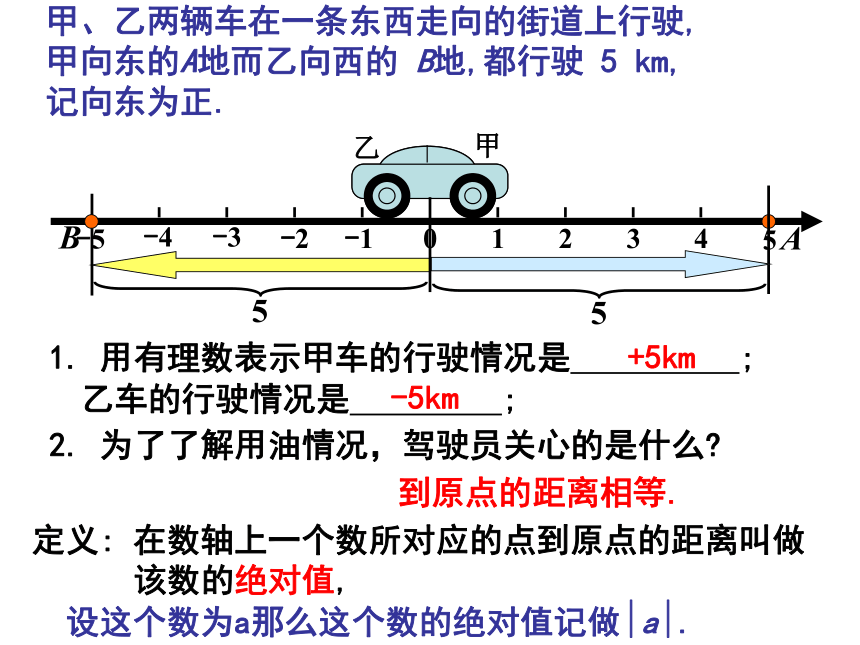
甲向东的A地而乙向西的 B地,都行驶 5 km,
记向东为正. 1. 用有理数表示甲车的行驶情况是 ; 01234-1-2-3-4-55BA2. 为了了解用油情况，驾驶员关心的是什么?+5km乙车的行驶情况是 ;-5km到原点的距离相等.定义: 在数轴上一个数所对应的点到原点的距离叫做
该数的绝对值,
设这个数为a那么这个数的绝对值记做?a?.2.表示2.8的点与原点的距离是　　，
即2.8的绝对值是　　,记作　　； 1.表示+7的点与原点的距离是　　,
即+7的绝值是　　,记作　　；3.表示0的点与原点的距离是　 　，
即0的绝对值是　 　,记作　　；4. 表示-5的点与原点的距离是　　，
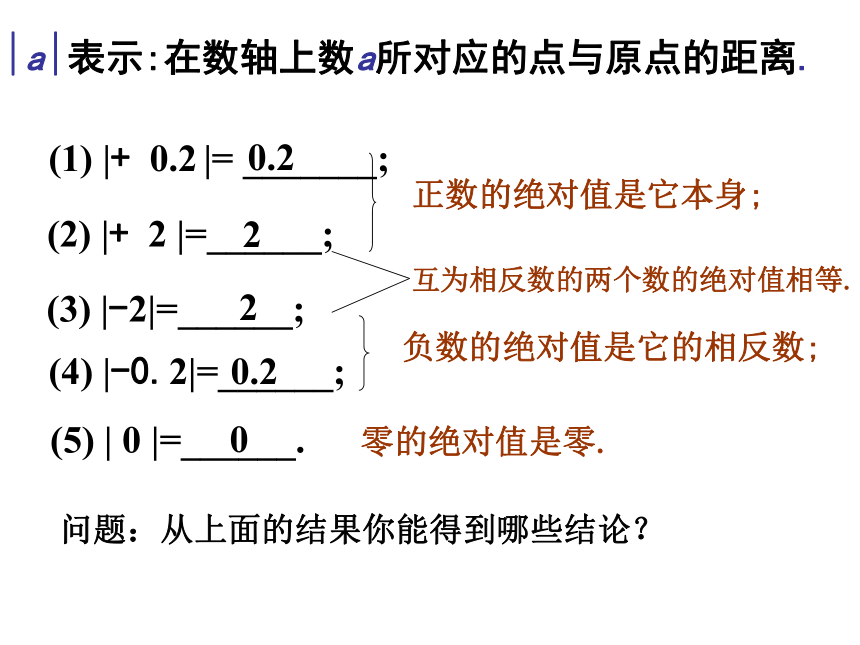
即-5的绝对值是　 　,记作　　； (1) |+ 0.2 |= _______;(2) |+ 2 |=______;(3) |-2|=______;0.22(4) |-0.2|=______;(5) | 0 |=______.020.2正数的绝对值是它本身;负数的绝对值是它的相反数;零的绝对值是零.互为相反数的两个数的绝对值相等.?a?表示:在数轴上数a所对应的点与原点的距离.问题：从上面的结果你能得到哪些结论？ 归纳与总结11:一个正数的绝对值是它本身；
2:一个负数的绝对值是它的相反数;
3:零的绝对值是零。
4互为相反数的两个数的绝对值相等。任何一个有理数的绝对值都是非负数:归纳与总结2：如果给定一个字母a，你能求出 | a | 吗？ (1) 如果a＞0, 那么| a |＝a; (2) 如果a＜0, 那么| a |＝－a; (3) 如果a＝0, 那么| a |＝0.也常常这样写:非负数的绝对值等于它本身.非正数的绝对值等于它的相反数.温馨提示：分类讨论请思考：设x是正有理数，化简|x|-x判断注意: 在考虑绝对值时，0是很容易被忽视的.例1：求下列各数的绝对值:解：计算：解：=4-4.54.59.69.600-8.78.76006000.4或-0.4-0.4或0.44或-4-4或4例2:求绝对值等于4的数.解: 方法一: 数轴法方法二:∵数轴上到原点距离等于4个单位长度的点有两个.如图:点P和点Q到原点的距离为4.∴绝对值等于4的数是＋4和－4.∴绝对值等于4的数是＋4和－4.思考：绝对值小于4的整数有几个？ 绝对值小于4的有理数有几个？0，1，2，3，－1，－2，－3无数个例3: 数轴上到4的距离等于5的数是多少?分析: 数轴是一条直线,要考虑两个方向.∵向正方向有: 4向右数5个单位后点对应的数是9向负方向有: 4向左数5个单位后点对应的数是－1解: ∴数轴上到4距离等于5的点对应的数有 9和－1.4+5=9,4－5=－1数轴上到-3的距离等于3的数是多少?由绝对值的定义:那么对任意的有理数a，b，| a | +| b | 呢?| a | +| b | ≥0对任意的有理数a, 总有| a |≥0.例4:对任意的有理数a，b，有| a | +| b |=0，求a,b的值?∵| a | ≥0, | b | ≥ 0∴由已知| a | +| b |=0可得: | a |=0,| b |=0∴ a=0, b=0解:| a - 2 | +| b + 3 |=0呢?a = 2 , b = －3?a?表示在数轴上, 数a所对应的点与原点的距离.已知a,b是有理数,且满足|a - 1|+ |b + 2|＝0,
试求a与b的值.a=1,b=-2已知a=-5,|a|=|b|，则b的值为＿＿+5或-5例5:已知|x|=3，|y|=2，求x+y的值。（1）已知|x|=3，|y|=2，x，y为异号
求x+y的值。（2）已知|x|=3，|y|=2，x，y为同号
求x+y的值。已知|a|=a，则a的值为＿＿已知|b|=-b，则b的值为＿＿已知|a|=a， |b|=-b，且|b|-a=0，试写出
符合条件的a，b检查了5个排球的重量（单位：克），其中超过标
标准重量的数量记为正数，不足的数量记为负数，
结果如下：其中哪个球的重量最接近标准？怎样用绝对值
解释排球的重量接近标准重量的程度？+根据绝对值的意义可知，数据的绝对值越小，说明排球重量越接近排球标准重量，与排球标准重量的偏差越小。所以选偏差的绝对值最小的根据绝对值的意义可知，绝对值越小越接近排球标准重量ABDCE|a| 和|a-b|的几何意义|a|=3 和|a-b|=3的几何意义|a|=3 和|a-1|=3求a的值1.有理数的绝对值的意义.
代数意义:一个正数的绝对值是它本身；
零的绝对值是零；
一个负数的绝对值是它的相反数.
几何意义:到原点的距离2.绝对值的性质：
3.绝对值与相反数的关系：
｜a｜≥０（非负性）互为相反数的两个数的绝对值相等；
绝对值相等，符号相反的两个数互为相反数；
若|a|=|b|，则a=b或者a=-b4.绝对值等于本身的数：
5.绝对值为非零数，则0和正数（非负数）原数有2个，且互为相反数(2)绝对值小于 10 的整数有（ ）个。(3)绝对值不大于 7 的负整数是（ ）。(1)绝对值等于4的数是( )+4, -4 19-1,-2,-3,-4,-5,-6,-7+1,-1,+2,-2（5） m 是有理数时,下列说法中正确的是
(A) -m 是负数 (B) |m|是正数
(C) |-m|是非负数 (D) -|m|是负数（6）若 |a| > a , 则 a 是
(A) 正数 (B) 负数
(C) 非正数 (D) 非负数（7）一个数的相反数的绝对值是正数,这个数一定是
(A) 非正数 (B) 非负数
(C) 非零数 (D)不能确定小结通过这节课，你学到了什么？（1）绝对值的概念（2） 绝对值?a?的几何意义：
在数轴上数a所对应的点与原点的距离.（3）相反数与倒数