二次函数复习
图片预览








文档简介
课件33张PPT。二次函数
复习一、概念形如y=ax2+bx+c (a,b,c是常数,a≠0) 的函数叫做二次函数其中二次项为ax2,一次项为bx,常数项c二次项的系数为a,一次项的系数为b,常数项c 1、下列函数中,哪些是二次函数?
(1)y=3x-1 (2)y=3x2
(3)y=3x3+2x2 (4)y=2x2-2x+1
(5)y=x -2 +x (6)y=x2-x(1+x)2、当m取何值时,函数是y= (m+2)x
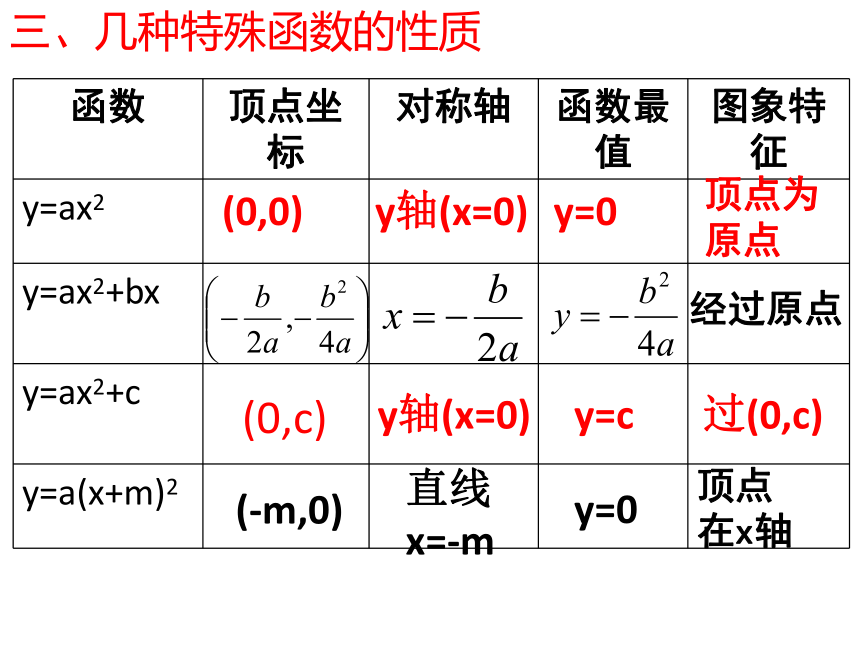
分别 是一次函数? 反比例函数? 二、二次函数的三种形式:一般式:y=ax2+bx+c顶点式:y=a(x+m)2+k交点式:y=a(x-x1)(x-x2)y=ax2+bx+cy=a(x+m)2+ky=a(x-x1)(x-x2)(-m,k)直线x=-my=k1、y=x22、y=(x-1)23、y=(x-1)2+34、y=-2(x+1)2-35、y=2x2+36、y=3x2-6x-5求下列函数的顶点坐标7、y=-2x2-4x+5(0,0)(1,0)(1,3)(-1,-3)(0,3)(2,-8)(-2,7)三、几种特殊函数的性质(0,0)y轴(x=0)y=0顶点为
原点经过原点(0,c)y轴(x=0)y=c过(0,c)(-m,0)直线
x=-my=0顶点
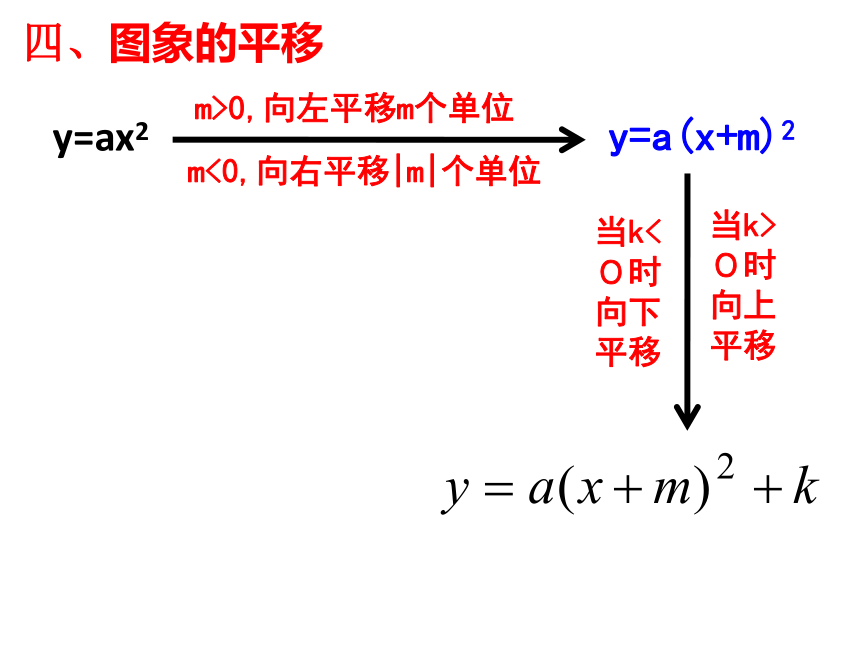
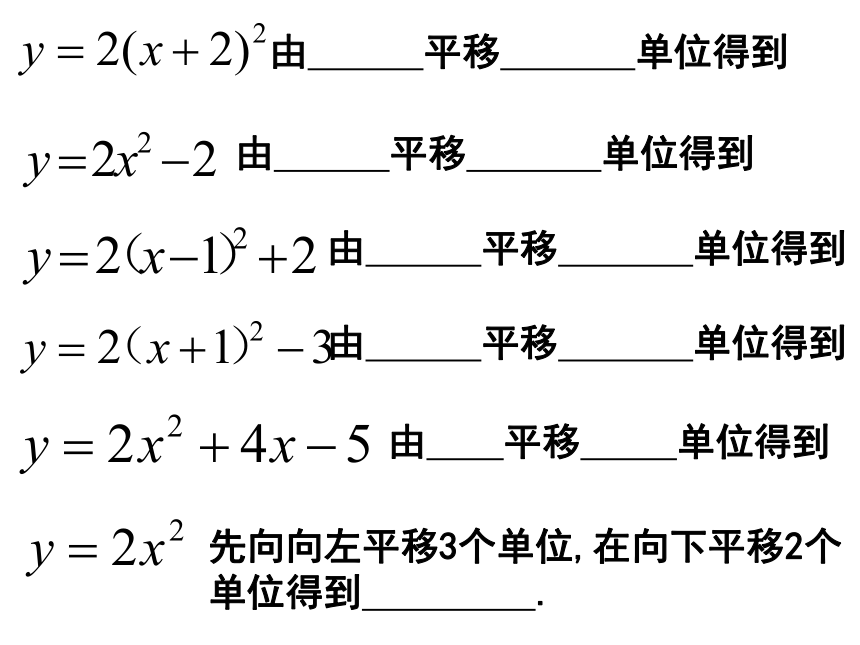
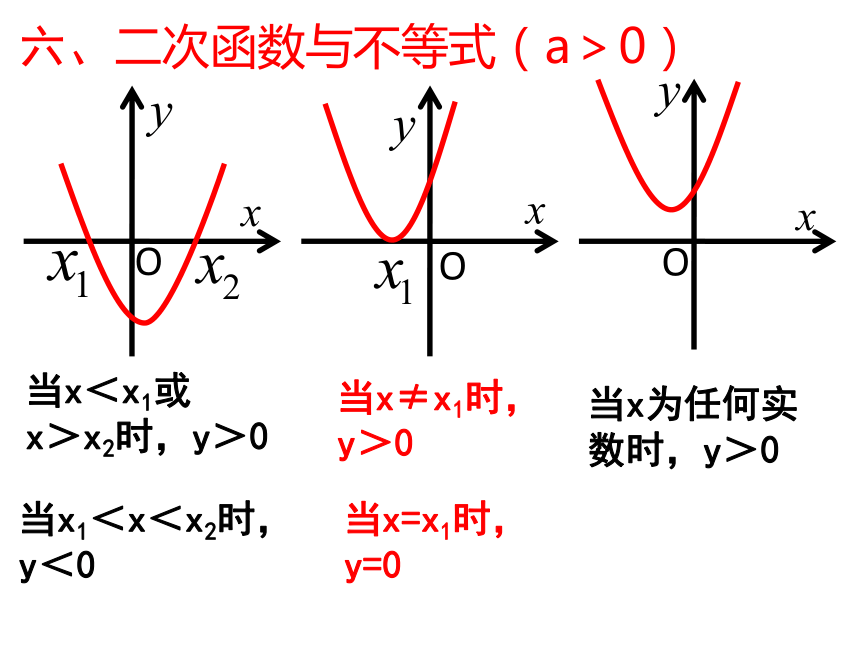
在x轴四、图象的平移y=ax2m<0,向右平移|m|个单位y=a(x+m)2m>0,向左平移m个单位当k>0时向上平移当k<0时向下平移y=ax2先向左(或右)平移|m|个单位再向上(或下)平移|k|个单位口诀:左正右负,上正下负y=ax2当K>0时向上平移k个单位当k<0时向下平移|k|个单位y=ax2+c五、求一次函数与二次函数的交点:y=kx+b与y=ax2+bx+c的交点:ax2+bx+c=kx+b2、可以根据y1=y2组成一个一元二次方程:六、二次函数与不等式(a>0)当x<x1或
x>x2时,y>0当x1<x<x2时,
y<0当x≠x1时,
y>0当x=x1时,y=0当x为任何实数时,y>01、已知二次函数y=-x2-4x+5,求当x为何值时,y>0,y=0,y<02、解不等式:(1) x2-4x-5>0
(2)-x2-4x+5>0 七、二次函数与一元二次方程的关系△>0,方程有两个实数根△=0,方程有两个相等实数根△<0,方程没有实数根填空:
(1)抛物线y=x2-3x+2与y轴的交点坐标是______,与x轴的交点坐标是_________;
(2)抛物线y=-2x2+5x-3与y轴的交点坐标是_______,与x轴的交点坐标是_____ __ _. (0,2)(1,0)和(2,0)(0,-3)(1,0)和(1.5,0) 根据下列表格的对应值:
判断方程ax2+bx+c=0(a≠0,a、b、c为常数)一个解的范围是 ( )
A、3<x<3.23 B、3.23<x<3.24
C、3.24<x<3.25 D、3.25<x<3.26C八、判别a、b、c、b2-4ac,2a+b,a+b+c的符号(1)a的符号:由抛物线的开口方向确定开口向上a>0开口向下a<0(2)b的符号:由对称轴的位置确定对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0(3)C的符号:由抛物线与y轴的交点位置确定.交点在x轴上方交点在x轴下方经过坐标原点c>0c<0c=0(4)b2-4ac的符号:由抛物线与x轴的交点个数确定与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<0练一练:已知y=ax2+bx+c的图象如图所示,
a___0, b____0, c_____0, abc____0
b___2a, 2a-b_____0, 2a+b_______0
b2-4ac_____0
a+b+c_____0, a-b+c____0
4a-2b+c_____0<<<<>>><>>>如图,直线y=2x+4与x轴、y轴分别交于A,B两点,把△OAB绕点O旋转900得到△OCD
(1)求经过A,B,D三点的抛物线的解析式;
(2)在所求的抛物线上是
否存在点P,使直线CP把
△OCD分成面积相等的两
部分?如果存在,求出点
P的坐标,如果不存在,
请说明理由。ABCDOxy例题解析一、填空题:1、若抛物线y=ax2+2x+c的顶点坐标是(2,3),则a= ,c= 。-0.512、抛物线y=2x2-4x-1是由抛物线y=2x2-bx+c向左平移1个单位,再向下平移2个单位得到的,则b= ,c= 。873、若二次函数y=(m-8)x2+2x+m2-64的图象过原点,则m= 。-84、已知抛物线y=2x2+bx+8的顶点在x轴上,则b= 。±85、如果点P(1,a)和点Q(-1,b)在抛物线y=-x2+1上,那么线段PQ的长为 。26、直线y=-2x-3与抛物线y=x2+(3m+1)x+2m的对称轴交于点(-2,1),则m= 。17、抛物线y=-(x-m)(x-3-k)+m与抛物线y=(x-3)2+4关于原点对称,则m+k= 。-98、若y=ax2+bx+c(a ? 0)与轴交于点A(2,0), B(4,0),则对称轴是_______直线x=39、把抛物线y=-3x2绕着它的顶点旋转1800后所得的图象解析式是 。y=3x210、已知二次函数y=a(x-h)2+k的图象过原点,最小值是-8,且形状与抛物线y=0.5x2-3x-5的形状相同,其解析式为 。y=0.5(x+4)2-8或y=0.5(x-4)2-811、函数y=ax2-ax+3x+1的图象与x轴有且只有一个交点,那么a的值和交点坐标分别为 , 。9或1二、选择题1、若y=ax2+bx+c(a ? 0)与X轴交于点A(2,m), B(6,m),则对称轴是_______
A 直线x=3 B 直线x=4
C 直线x= -3 D 直线x=2BB三、求二次函数的解析式1、已知一个二次函数的图象经过点
(0,0),(1,﹣3),(2,﹣8)。2、已知二次函数的图象的顶点坐标为
(-2,-3),且图象过点(-3,-2)。3、已知二次函数的图象的对称轴是直线x=3,
并且经过点(6,0),和(2,12)4、二次函数的图象过(4,-3),(2,1),
(-1,-8)三点。5、图象过(2,0),(-5,0),(1,4)
三点。 7、已知二次函数y=ax2+bx+c的最大值是2,
图象顶点在直线y=x+1上,并且图象经过
点(3,-6)6、设抛物线 过点(0, 5), 且顶点坐标为(1,3),
求抛物线的解析式.9、已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的
形状相同,顶点在直线x=1上,且顶点到x轴的距离
为5,请写出满足此条件的抛物线的解析式.解:?抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状
相同? a=1或-1
又?顶点在直线x=1上,且顶点到x轴的距离为5,
? 顶点为(1,5)或(1,-5)
所以其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5
四、综合题1、已知抛物线y=x2-2x-8, (1)求证:该抛物线与x轴一定有两个交点; (2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积。 2、已知抛物线y=ax2+bx+c与x轴正、负半轴分别交于A、B两点,与y轴负半轴交于点C。若OA=4,OB=1,∠ACB=90°,求抛物线解析式。3、某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?4、已知:如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点c(0,4),与x轴交于点A,B,点A的坐标为(4,0)
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q做QE∥AC,交BC于点E,连接CQ,当△COE的面积最大时,求点Q的坐标;
(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点的坐标为(2,0)问:是否存在这样的直线l,使得△ODF是等腰三角形?,若存在,请求出点P的坐标,若不存在,请说明理由。ABCEQOxy5、如图,在平面直角坐标系中,O为原点,点AC的坐标分别为(2,0)(1, ),将△OAC绕中点旋转1800,点O落在点B的位置,抛物线y=ax2-2 经过点A,点D是该抛物线的顶点。
(1)求a的值,点B的坐标;
(2)若点P是线段OA上的一点,且∠APO=∠OAB,求点P的坐标;
()3若点P是x轴上的一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点在y轴上,写出点P的坐标。ABCxyOD6、如图,抛物线y=x2-2x-3与x轴交于A、B两点(A点在B点的左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2。
(1)求A、B两点的坐标及直线AC的函数解析式;
(2)P是线段AC上的一个动点,过点P作y轴的平行线交抛物线与E点,求线段PE的长的最大值。
(3)点G是抛物线上的动点,在x轴上是否存在F,使以A、C、F、G四点为顶点的四边形是平行四边形?若存在,求出所有满足条件的点F的坐标,若不存在,请说明理由。ABCOxyP再见
复习一、概念形如y=ax2+bx+c (a,b,c是常数,a≠0) 的函数叫做二次函数其中二次项为ax2,一次项为bx,常数项c二次项的系数为a,一次项的系数为b,常数项c 1、下列函数中,哪些是二次函数?
(1)y=3x-1 (2)y=3x2
(3)y=3x3+2x2 (4)y=2x2-2x+1
(5)y=x -2 +x (6)y=x2-x(1+x)2、当m取何值时,函数是y= (m+2)x
分别 是一次函数? 反比例函数? 二、二次函数的三种形式:一般式:y=ax2+bx+c顶点式:y=a(x+m)2+k交点式:y=a(x-x1)(x-x2)y=ax2+bx+cy=a(x+m)2+ky=a(x-x1)(x-x2)(-m,k)直线x=-my=k1、y=x22、y=(x-1)23、y=(x-1)2+34、y=-2(x+1)2-35、y=2x2+36、y=3x2-6x-5求下列函数的顶点坐标7、y=-2x2-4x+5(0,0)(1,0)(1,3)(-1,-3)(0,3)(2,-8)(-2,7)三、几种特殊函数的性质(0,0)y轴(x=0)y=0顶点为
原点经过原点(0,c)y轴(x=0)y=c过(0,c)(-m,0)直线
x=-my=0顶点
在x轴四、图象的平移y=ax2m<0,向右平移|m|个单位y=a(x+m)2m>0,向左平移m个单位当k>0时向上平移当k<0时向下平移y=ax2先向左(或右)平移|m|个单位再向上(或下)平移|k|个单位口诀:左正右负,上正下负y=ax2当K>0时向上平移k个单位当k<0时向下平移|k|个单位y=ax2+c五、求一次函数与二次函数的交点:y=kx+b与y=ax2+bx+c的交点:ax2+bx+c=kx+b2、可以根据y1=y2组成一个一元二次方程:六、二次函数与不等式(a>0)当x<x1或
x>x2时,y>0当x1<x<x2时,
y<0当x≠x1时,
y>0当x=x1时,y=0当x为任何实数时,y>01、已知二次函数y=-x2-4x+5,求当x为何值时,y>0,y=0,y<02、解不等式:(1) x2-4x-5>0
(2)-x2-4x+5>0 七、二次函数与一元二次方程的关系△>0,方程有两个实数根△=0,方程有两个相等实数根△<0,方程没有实数根填空:
(1)抛物线y=x2-3x+2与y轴的交点坐标是______,与x轴的交点坐标是_________;
(2)抛物线y=-2x2+5x-3与y轴的交点坐标是_______,与x轴的交点坐标是_____ __ _. (0,2)(1,0)和(2,0)(0,-3)(1,0)和(1.5,0) 根据下列表格的对应值:
判断方程ax2+bx+c=0(a≠0,a、b、c为常数)一个解的范围是 ( )
A、3<x<3.23 B、3.23<x<3.24
C、3.24<x<3.25 D、3.25<x<3.26C八、判别a、b、c、b2-4ac,2a+b,a+b+c的符号(1)a的符号:由抛物线的开口方向确定开口向上a>0开口向下a<0(2)b的符号:由对称轴的位置确定对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0(3)C的符号:由抛物线与y轴的交点位置确定.交点在x轴上方交点在x轴下方经过坐标原点c>0c<0c=0(4)b2-4ac的符号:由抛物线与x轴的交点个数确定与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<0练一练:已知y=ax2+bx+c的图象如图所示,
a___0, b____0, c_____0, abc____0
b___2a, 2a-b_____0, 2a+b_______0
b2-4ac_____0
a+b+c_____0, a-b+c____0
4a-2b+c_____0<<<<>>><>>>如图,直线y=2x+4与x轴、y轴分别交于A,B两点,把△OAB绕点O旋转900得到△OCD
(1)求经过A,B,D三点的抛物线的解析式;
(2)在所求的抛物线上是
否存在点P,使直线CP把
△OCD分成面积相等的两
部分?如果存在,求出点
P的坐标,如果不存在,
请说明理由。ABCDOxy例题解析一、填空题:1、若抛物线y=ax2+2x+c的顶点坐标是(2,3),则a= ,c= 。-0.512、抛物线y=2x2-4x-1是由抛物线y=2x2-bx+c向左平移1个单位,再向下平移2个单位得到的,则b= ,c= 。873、若二次函数y=(m-8)x2+2x+m2-64的图象过原点,则m= 。-84、已知抛物线y=2x2+bx+8的顶点在x轴上,则b= 。±85、如果点P(1,a)和点Q(-1,b)在抛物线y=-x2+1上,那么线段PQ的长为 。26、直线y=-2x-3与抛物线y=x2+(3m+1)x+2m的对称轴交于点(-2,1),则m= 。17、抛物线y=-(x-m)(x-3-k)+m与抛物线y=(x-3)2+4关于原点对称,则m+k= 。-98、若y=ax2+bx+c(a ? 0)与轴交于点A(2,0), B(4,0),则对称轴是_______直线x=39、把抛物线y=-3x2绕着它的顶点旋转1800后所得的图象解析式是 。y=3x210、已知二次函数y=a(x-h)2+k的图象过原点,最小值是-8,且形状与抛物线y=0.5x2-3x-5的形状相同,其解析式为 。y=0.5(x+4)2-8或y=0.5(x-4)2-811、函数y=ax2-ax+3x+1的图象与x轴有且只有一个交点,那么a的值和交点坐标分别为 , 。9或1二、选择题1、若y=ax2+bx+c(a ? 0)与X轴交于点A(2,m), B(6,m),则对称轴是_______
A 直线x=3 B 直线x=4
C 直线x= -3 D 直线x=2BB三、求二次函数的解析式1、已知一个二次函数的图象经过点
(0,0),(1,﹣3),(2,﹣8)。2、已知二次函数的图象的顶点坐标为
(-2,-3),且图象过点(-3,-2)。3、已知二次函数的图象的对称轴是直线x=3,
并且经过点(6,0),和(2,12)4、二次函数的图象过(4,-3),(2,1),
(-1,-8)三点。5、图象过(2,0),(-5,0),(1,4)
三点。 7、已知二次函数y=ax2+bx+c的最大值是2,
图象顶点在直线y=x+1上,并且图象经过
点(3,-6)6、设抛物线 过点(0, 5), 且顶点坐标为(1,3),
求抛物线的解析式.9、已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的
形状相同,顶点在直线x=1上,且顶点到x轴的距离
为5,请写出满足此条件的抛物线的解析式.解:?抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状
相同? a=1或-1
又?顶点在直线x=1上,且顶点到x轴的距离为5,
? 顶点为(1,5)或(1,-5)
所以其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5
四、综合题1、已知抛物线y=x2-2x-8, (1)求证:该抛物线与x轴一定有两个交点; (2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积。 2、已知抛物线y=ax2+bx+c与x轴正、负半轴分别交于A、B两点,与y轴负半轴交于点C。若OA=4,OB=1,∠ACB=90°,求抛物线解析式。3、某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价一元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?4、已知:如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点c(0,4),与x轴交于点A,B,点A的坐标为(4,0)
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q做QE∥AC,交BC于点E,连接CQ,当△COE的面积最大时,求点Q的坐标;
(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点的坐标为(2,0)问:是否存在这样的直线l,使得△ODF是等腰三角形?,若存在,请求出点P的坐标,若不存在,请说明理由。ABCEQOxy5、如图,在平面直角坐标系中,O为原点,点AC的坐标分别为(2,0)(1, ),将△OAC绕中点旋转1800,点O落在点B的位置,抛物线y=ax2-2 经过点A,点D是该抛物线的顶点。
(1)求a的值,点B的坐标;
(2)若点P是线段OA上的一点,且∠APO=∠OAB,求点P的坐标;
()3若点P是x轴上的一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点在y轴上,写出点P的坐标。ABCxyOD6、如图,抛物线y=x2-2x-3与x轴交于A、B两点(A点在B点的左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2。
(1)求A、B两点的坐标及直线AC的函数解析式;
(2)P是线段AC上的一个动点,过点P作y轴的平行线交抛物线与E点,求线段PE的长的最大值。
(3)点G是抛物线上的动点,在x轴上是否存在F,使以A、C、F、G四点为顶点的四边形是平行四边形?若存在,求出所有满足条件的点F的坐标,若不存在,请说明理由。ABCOxyP再见
同课章节目录
