2.4二次函数的应用

课件12张PPT。2.4 二次函数的应用⑴浙教版九年级上册第二章二次函数1.已知抛物线y=x2-2x-3与x轴交于
A,B两点,与y轴交于C点.
(1)求A,B,C三点的坐标. (2)求S△ABC的值．
(3)当x取何值时,y>0?何值时y<0.
(4)求函数y＝x2-2x－3的最值。回顾:抛物线在什么位置取最值？1。无取值范围限制的，在顶点处取最值。
2。有取值范围的在端点和顶点处取最值。2、图中所示的二次函数图像的解析式为： y=2x2+8x+13
=2（x+2）2+5
⑴若－3≤x≤0，该函数的最大值、最小值分别　为（ ）、（ ）。⑵又若-4≤x≤-3，该函数的最大值、最小值分别为（ ）、（ ）。求函数的最值问题，应注意对称轴是否在自变量的取值范围内。131313(-4,13)(-2,5)57给你长6m的铝合金条，设问：
①你能用它制成一矩形窗框吗？
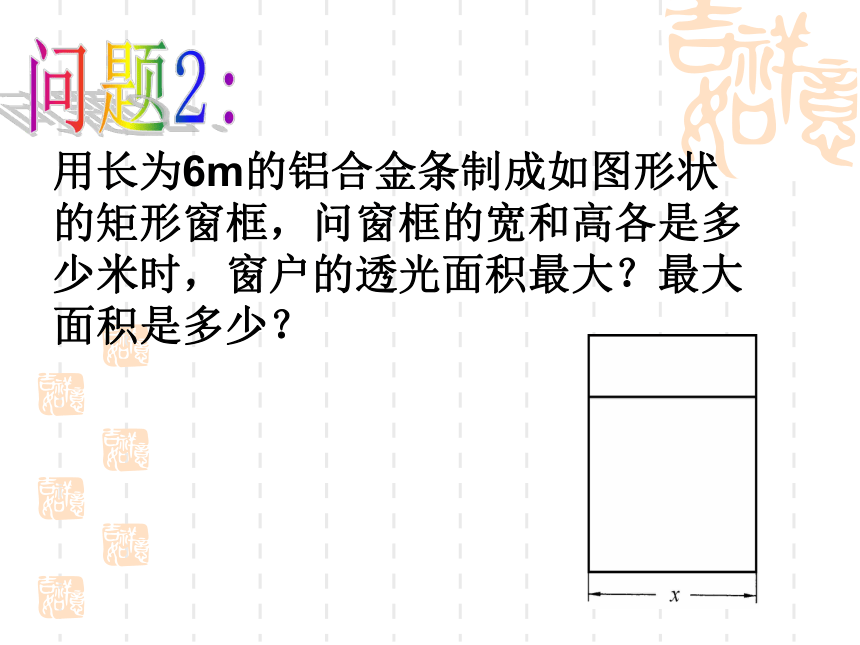
②怎样设计，窗框的透光面积最大？问题1:x3-xy=x(3-x)=-x2 +3x(0＜x＜3)解:设宽为x米,窗框的透光面积ym2根据题意得,当x = 时,y有最大值是用长为6m的铝合金条制成如图形状的矩形窗框，问窗框的宽和高各是多少米时，窗户的透光面积最大？最大面积是多少？问题2:步骤：
数学建模第二步建立函数的解析式；
第三步确定自变量的取值范围；
第四步根据顶点坐标公式或配方法
求出最大值或最小值（在自变量的
取值范围内）第一步设自变量；在用长为6米的铝合金条制成如图所示的窗框（把矩形的窗框改为上部分是由4个全等扇形组成的半圆，下部分是矩形），那么如何设计使窗框的透光面积最大？（结果精确到0.01米）问题3:在矩形荒地ABCD中，AB=10，BC=6,今在四边上分别选取E、F、G、H四点，且AE=AH=CF=CG=x，建一个花园，如何设计，可使花园面积最大？106解：设花园的面积为y
则 y=60-x2 –(10-x)(6-x)=-2x2 + 16x（0点P从点A开始沿AB边向点B以2厘米／秒的速度移动，
点Q从点B开始沿BC边向点C以1厘米／秒的速度
移动，如果P,Q分别从A,B同时出发，
几秒后ΔPBQ的面积最大？
最大面积是多少？小试牛刀解：根据题意，设经过x秒后ΔPBQ的面积y最大AP=2x cm PB=（8-2x ） cm QB=x cm则 y=1/2 x（8-2x）=-x2 +4x=-（x2 -4x +4 -4）= -（x - 2）2 + 4所以，当P、Q同时运动2秒后ΔPBQ的面积y最大
最大面积是 4 cm2（0