3.2实数

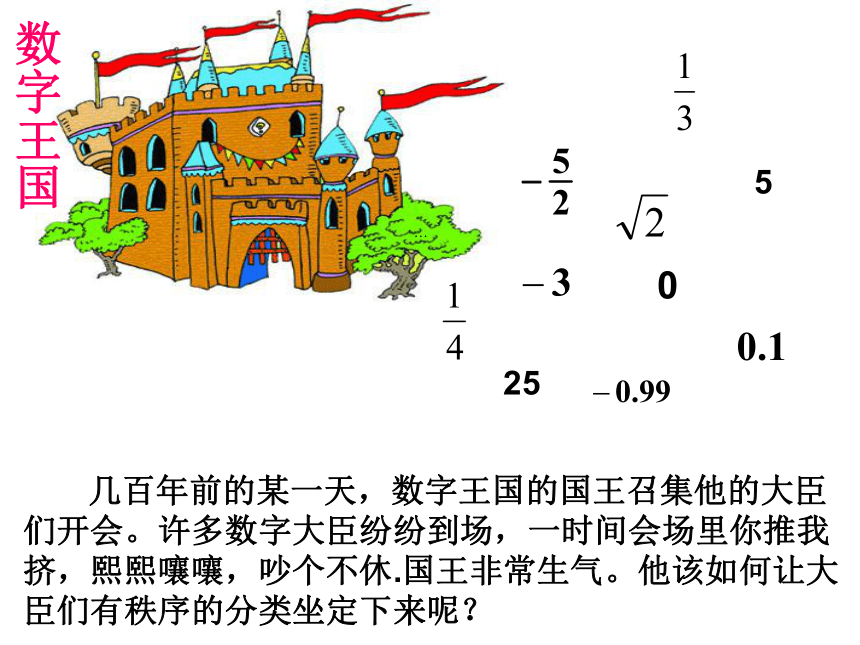
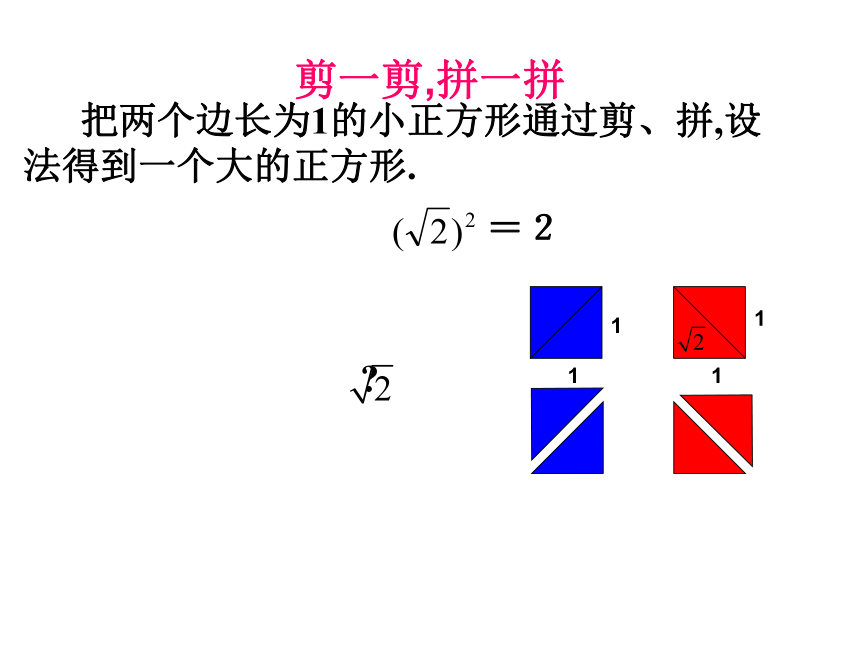
课件16张PPT。实数数字王国 几百年前的某一天，数字王国的国王召集他的大臣们开会。许多数字大臣纷纷到场，一时间会场里你推我挤，熙熙嚷嚷，吵个不休.国王非常生气。他该如何让大臣们有秩序的分类坐定下来呢？ 剪一剪,拼一拼 把两个边长为1的小正方形通过剪、拼,设法得到一个大的正方形.?＝２1111探究活动： 3.形如
的数字你能举出些类似的无理数吗？1.01001000100001…
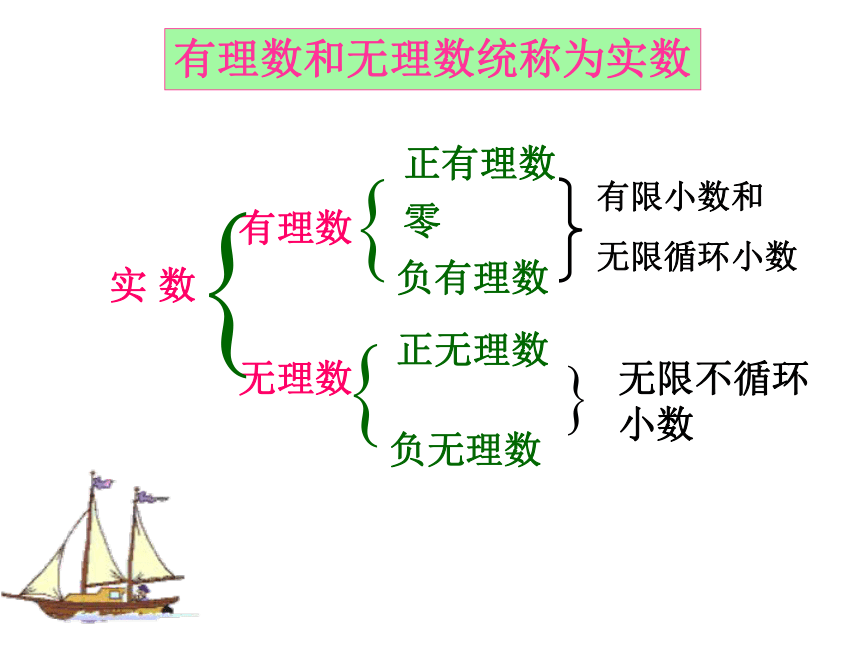
（两个1之间依次多一个0）正有理数负有理数零负无理数正无理数有理数无理数实 数无限不循环小数有限小数和
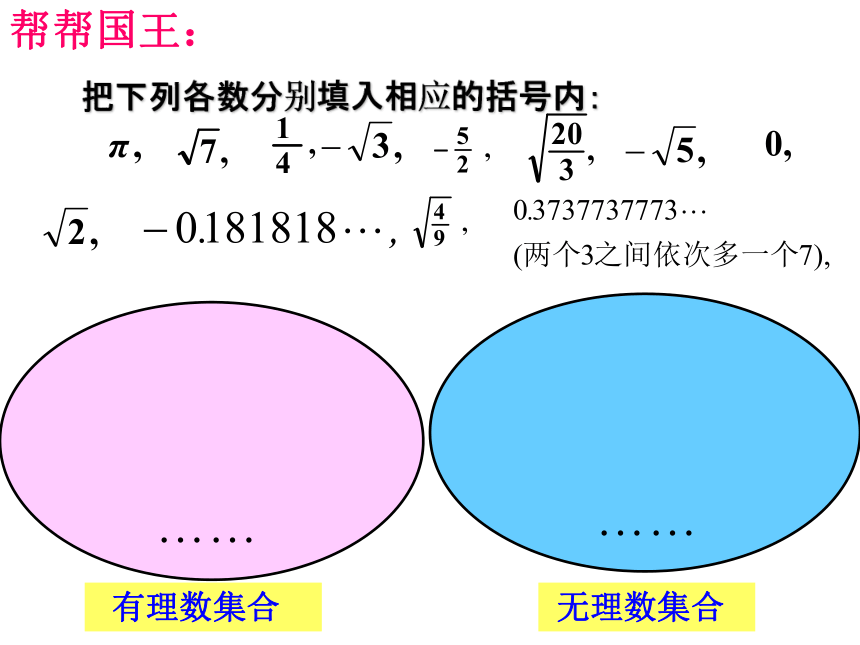
无限循环小数有理数和无理数统称为实数 把下列各数分别填入相应的括号内： 有理数集合 无理数集合帮帮国王：π 我们坐在哪里啊国王出招：-1.41.5重要提示与 是互为相反数由图可得： ＜1.4＜ ＜1.5＜∏＜3.3 你能将 1.5 , , , 3.3 , π , -1.4 按从小到大的顺序排列吗？ 在数轴上表示的两个实数，右边的数总比左边的数大。重要提示一一对应每一个实数都可以用数轴上的一个点来表示。实数 a实数数轴上的点 反过来，数轴上的每一个点都表示一个实数。重要提示国王出题：判断下列说法是否正确，并举例说明理由.
①两个无理数的和一定是无理数；
②两个无理数的积一定是无理数；
感悟反思通过这节课的学习活动你有哪些收获？
1、无理数和实数的概念；2、实数的分类；3、实数和数轴上的点是一一对应的；4、相反数、绝对值、数的大小比较法则同样适用于实数；“海神错判” 约公元600年，毕达哥拉斯学派认为宇宙万物的总规律是服从整数化，认为世界上一切现象，都能归结为整数或整数之比。正当毕氏学派津津乐道地高唱“万物皆数”时，该学派的一位成员希伯索斯利用推理的方法发现，边长为1的正方形的对角线长既不是整数，也不是整数的比（分数）所能表示的.这个发现被人们看成是“荒谬”和违反常识的事。对于只有整数和整数比概念的他们来说，这意味着边长为1的正方形的对角线长竟然不能用任何“数”来表示！这在数学史上称为第一次数学危机。最后希伯索斯的发现没有被毕达哥拉斯学派的信徒所接受，相传就因为这一发现，毕达哥拉斯学派把希伯索斯投入大海中处死。 布置作业1、必做题：课本第67页A组、B组题。
2、选做题：课本第67页C组题。
3、 作业题:p14