2。2二次函数的图象（2）

(共18张PPT)
课程标准浙教版实验教科书
九年级 上 册
二次函数的图象⑵
2.2
知识回顾:
二次函数y=ax 的图象及其特点
顶点坐标：（0，0） 对称轴： y轴
图象具有以下特点：
一般地，二次函数y=ax （ a≠0 ）的图象是一条抛物线；
当a>0 时，抛物线开口向上，顶点是抛物线上的最低点；
抛物线在x轴的上方（除顶点外）。
当a<0 时，抛物线开口向下，顶点是抛物线上的最高点。
抛物线在x轴的下方（除顶点外）
课前热身：
1、对于任意实数x，二次函数 的值总是非负数，则a得取值范围是（ ）
A.a≥－1 B. a≤－1 C. a > －1 D.a<－1
2、已知抛物线 与 关于x轴对称，则a = .
3、若抛物线 的开口向下，则m= .
3、若抛物线 的开口向下，则m= .
4、若抛物线 经过点A（m,n），则它也经过点（ ）
A.（－m，n） B.（m，－n） C.（ n ，m） D.（－n，m ）
5、已知（a，8）在抛物线 上，则a的值为 （ ）
A. 2 B. －2 C.±2 D.
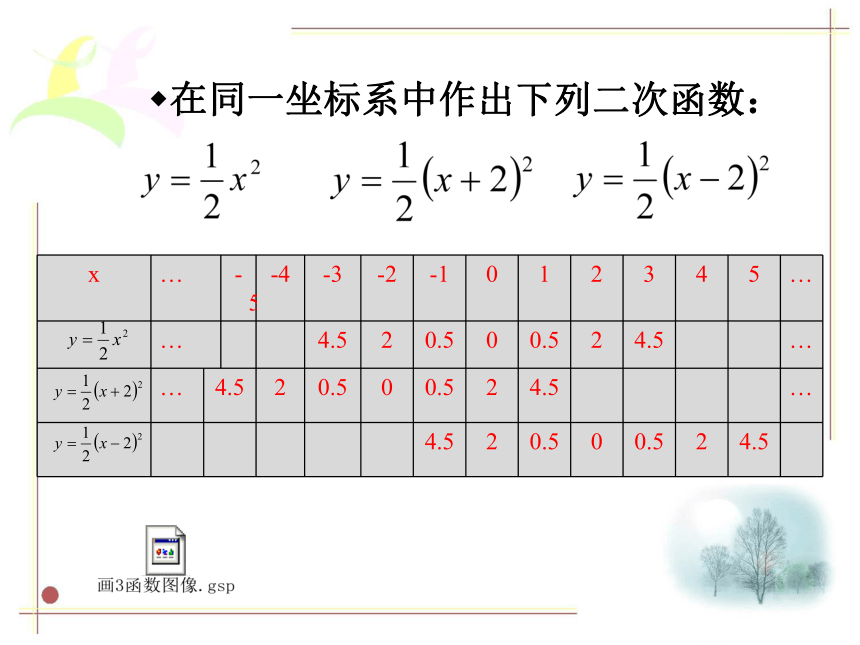
在同一坐标系中作出下列二次函数：
x … -5 -4 -3 -2 -1 0 1 2 3 4 5 …
… 4.5 2 0.5 0 0.5 2 4.5 …
… 4.5 2 0.5 0 0.5 2 4.5 …
4.5 2 0.5 0 0.5 2 4.5
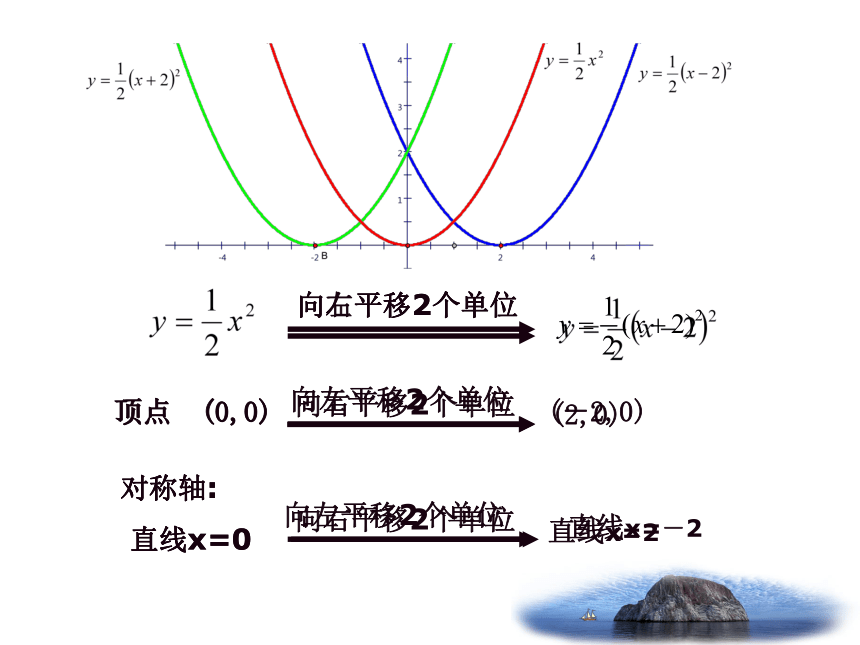
向右平移2个单位
顶点 (0,0)
(2,0)
对称轴:
直线x=0
直线x=2
向右平移2个单位
向右平移2个单位
向左平移2个单位
顶点 (0,0)
(－2,0)
对称轴:
直线x=0
直线x=－2
向左平移2个单位
向左平移2个单位
例1
对于二次函数
请回答下列问题：
1、把函数 的图象作怎样的平移
变换，就能得到函数 的图象。
2、说出函数 的图象的顶点坐标
和对称轴。
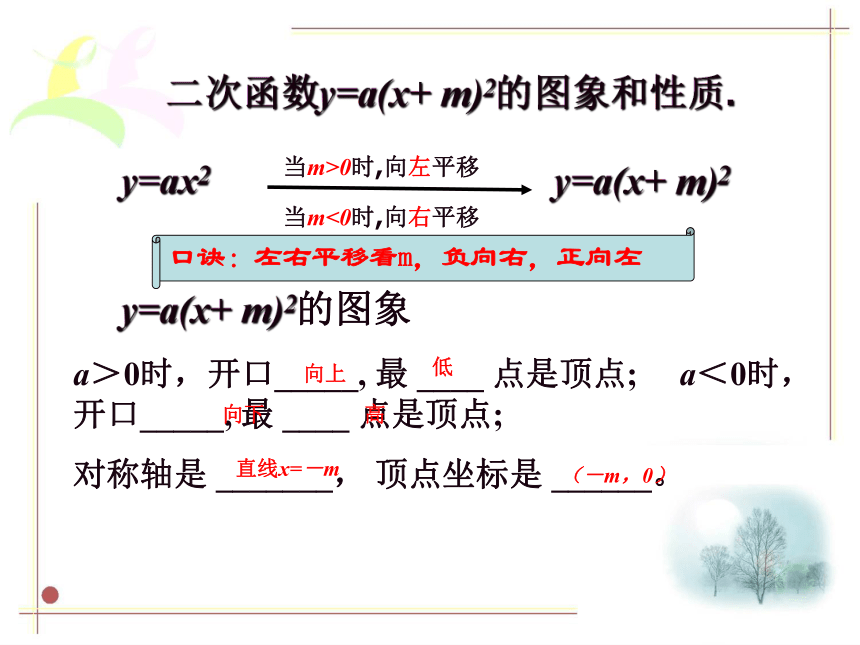
二次函数y=a(x+ m)2的图象和性质.
当m>0时,向左平移
当m<0时,向右平移
a＞0时，开口_____, 最 ____ 点是顶点; a＜0时，开口_____, 最 ____ 点是顶点;
对称轴是 _______， 顶点坐标是 ______。
y=ax2
y=a(x+ m)2的图象
y=a(x+ m)2
口诀：左右平移看m，负向右，正向左
直线x=－m
（－m，0）
向上
向下
低
高
做一做:
抛物线 开口方向 对称轴 顶点坐标
y =2(x+3)2
y = -3(x-1)2
y = -4(x-3)2
向上
直线x=－3
( －3 , 0 )
直线x=1
直线x=3
向下
向下
( 1 , 0 )
( 3, 0)
填空：
1、由抛物线y=2x 向 平移 个单位可得到y= 2(x +1)2
2、函数y= －5(x －4)2 的图象。可以由抛物线
向 平移 ________个单位而得到的。
用描点法在同一直角坐标系中画出下列函数的图象：
x … -5 -4 -3 -2 -1 0 1 …
… 4.5 2 0.5 0 0.5 2 4.5 …
… 7.5 5 3.5 3 3.5 5 7.5 …
二次函数y=a(x+ m)2+k的图象和性质.
当k>0时,向上平移
当k<0时,向下平移
a＞0时，开口_____, 最 ____ 点是顶点; a＜0时，开口_____, 最 ____ 点是顶点;
对称轴是 _______， 顶点坐标是 ______。
y=a(x+m)2
y=a(x+ m)2+k的图象
y=a(x+ m)2+k
口诀：上下平移有k，正向上，负向下
向上
低
向下
高
直线X=－m
(－m，k）
由函数 图象经过怎样平移得到函数
的图像
合作学习
讨论归纳:
y=a(x+m)2+k的图象：
对称轴是 _________，顶点坐标是 _______。
直线x=－m
(－m, k)
当k>0时,向上平移
当k<0时,向下平移
y=a(x+m)2
y=a(x+ m)2+k
当m>0时,向左平移
当m<0时,向右平移
y=ax2
y=a(x+ m)2
口诀：左右平移看m，负向右，正向左
上下平移有k，正向上，负向下
一般地，平移二次函数y=ax2的图象就可得到二次函数y=a(x+m)2+k的图象。因此，二次函数y=a(x+m)2+k它的形状、对称轴、顶点坐标和开口方向与a、m、k的值有关。
当堂检测：
1、二次函数 的对称轴 ，开口方向 ，顶点坐标 .
2、函数 向下 移动2个单位的抛物线是
，再向右平移一个单位的抛物线是 。
3、一个二次函数的顶点坐标是（2，1），它的形状及开口与抛物线 相同，这个二次函数的解析式是 .
4、将二次函数 的图象通过平移得到函数 的图象，则平移的方法的是 .
3