2.5 有理数的乘方（1）

课件17张PPT。2.5 有理数的乘方小故事： 传说在古代，有一位大臣为国王发明了一种象棋国王大喜，要对大臣进行奖赏，就问大臣有什么要求，大臣说；在象棋棋盘上放一些米，第1格放1粒米，第2格放2粒米，第3格
放4粒米，第4格放8粒米，
……，一直放到64格。国
王爽快地答应了。请问：
国王总共要放多少粒米？
他的王国一年生产的大米
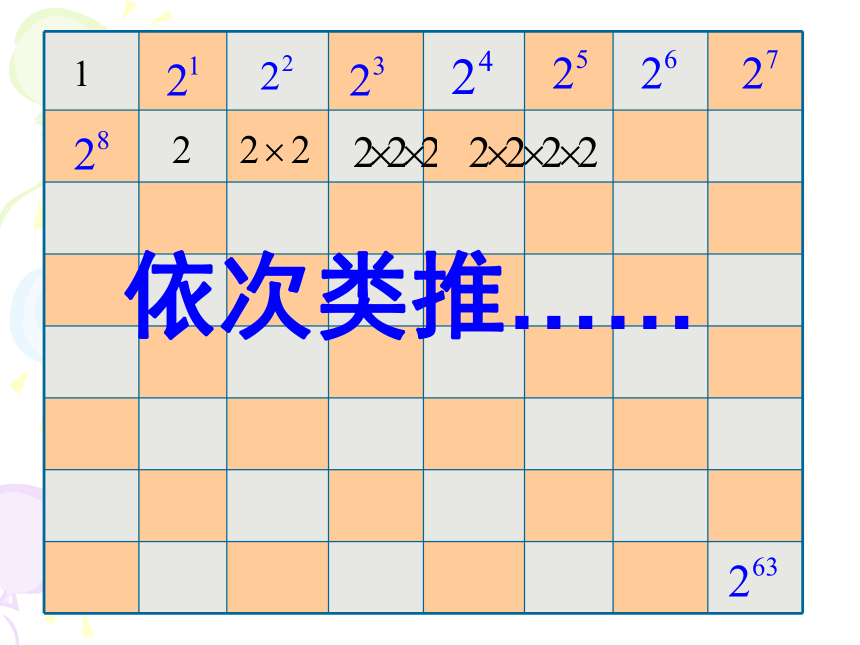
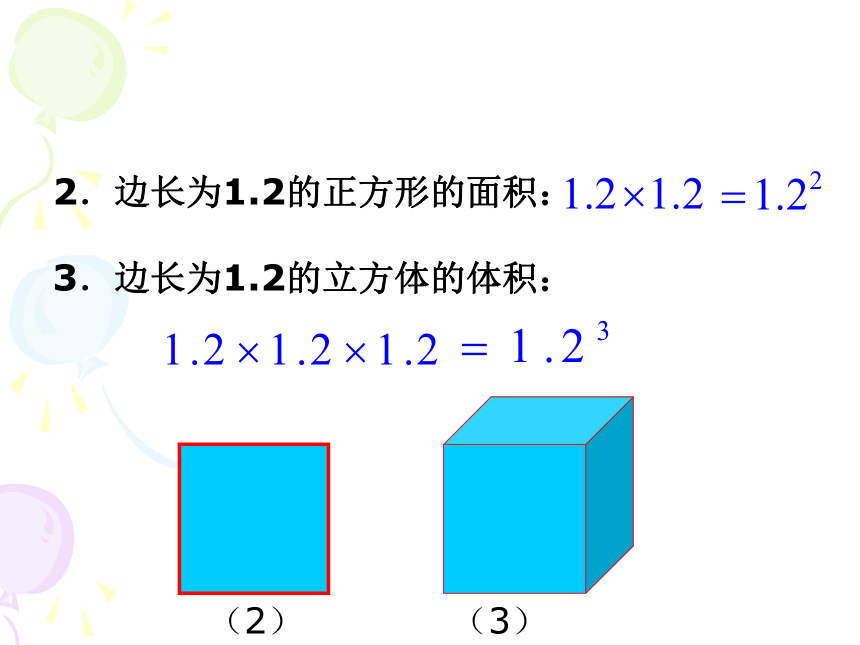
够吗？依次类推……2．边长为1.2的正方形的面积：　　　　
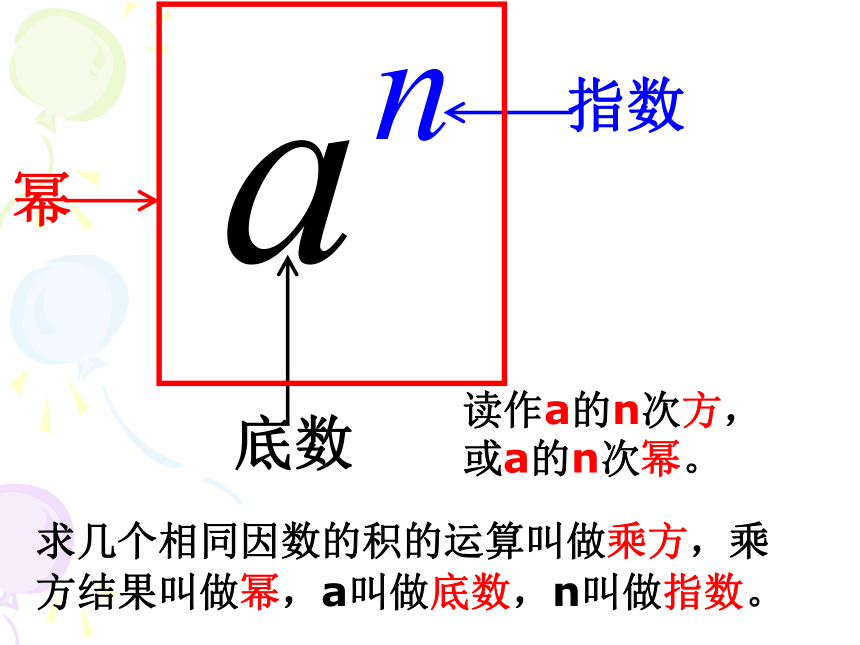
3．边长为1.2的立方体的体积：　　　　　　（2）（3）练习 B底数指数幂读作a的n次方，或a的n次幂。求几个相同因数的积的运算叫做乘方，乘方结果叫做幂，a叫做底数，n叫做指数。练习：
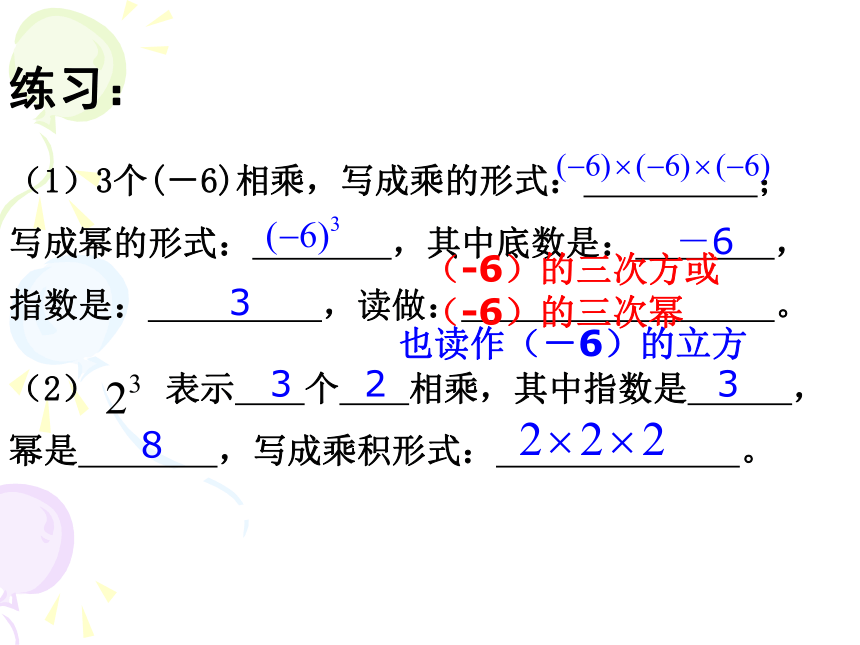
（1）3个(－6)相乘，写成乘的形式：　　　　　；　　写成幂的形式：　　　　，其中底数是：　　　　，　指数是：　　　　　，读做：　　　　　　　　　。
（2）　　表示　　个　　相乘，其中指数是　　　，　幂是　　　　，写成乘积形式：　　　　　　　。－63也读作（－6）的立方3238（-6）的三次方或（-6）的三次幂例1　计算：
练习　1.计算：
2.计算（口答）
2483216＋4－2－32＋16－8幂的符号规律：
1．正数的任何次幂都是正数。
2．负数的偶次幂是正数，负数的奇次幂是负数。3、计算并找规律：
（1）102，103，104，105
（2）（-10）2，（-10）3，
（-10）4，（-10）5
（3）0.12，0.13，0.14，0.15
（4）（-0.1）2，（-0.1）3，
（-0.1）4，（-0.1）5上述计算结果，有什么规律？ 乘除和乘方混合运算顺序：　　　　　　　　　　　　　　　　　　　　　　　　先算乘方，后算乘除；如果遇到括号，就先进行括号里的运算。例2　计算：
练习　计算：
小结：
1．乘方：求相同因数的积的运算。
　　运算时，先定符号，再算绝对值。
2．幂的底数是分数或负数时，底数应添　　　　　　上括号。
3．注意：
拓展练习：1、计算（-2）2006－220054、若有理数a满足（2002-a）2008=1，则a 的值是什么？7、观察下列各式：
22-12=（2+1）（2-1）
32-22=（3+2）（3-2）
42-32=（4+3）（4-3）
试计算：19512-19502+19532-19522+……20072-200626、77+77+77+77+77+77+778、计算：
（1）3+32+33+34+……+32004