2.2等腰三角形的性质

课件29张PPT。
2.2 等腰三角形的性质引入新课：什么叫等腰三角形？等腰三角形是什么对称
图形？它的对称轴是什么？复习提问：两边相等的三角形
叫做等腰三角形；等腰三角形是轴对称图形；轴对称是等腰三角形的
顶角平分线所在的直线。底边返回菜单复习提问：将一把三角尺和一个重锤如图放置，就能检查
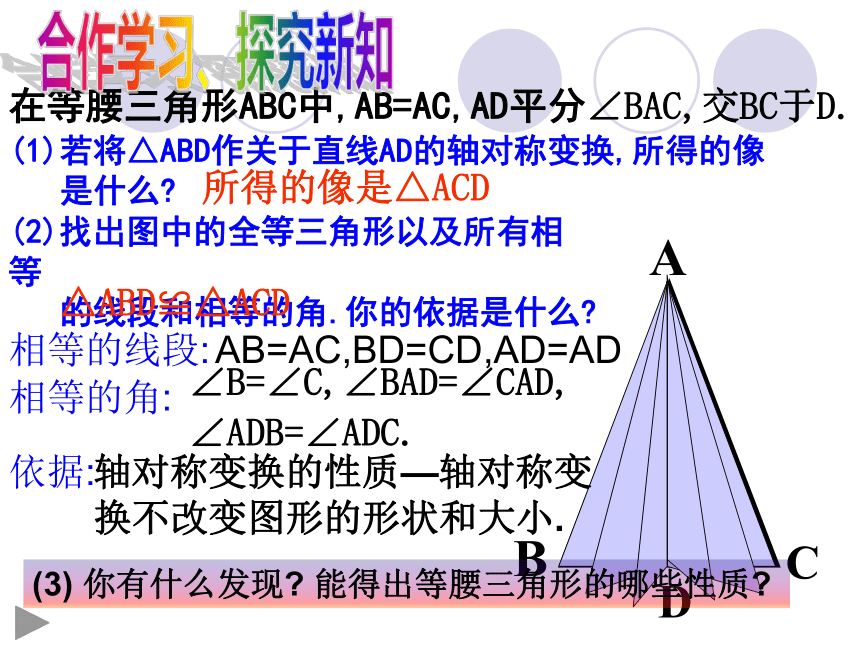
一根横梁是否水平，你知道为什么吗？返回菜单在等腰三角形ABC中,AB=AC,AD平分∠BAC,交BC于D.(1)若将△ABD作关于直线AD的轴对称变换,所得的像
是什么?(2)找出图中的全等三角形以及所有相等
的线段和相等的角.你的依据是什么?所得的像是△ACD△ABD≌△ACD相等的线段:AB=AC,BD=CD,AD=AD相等的角:∠B=∠C,∠BAD=∠CAD,
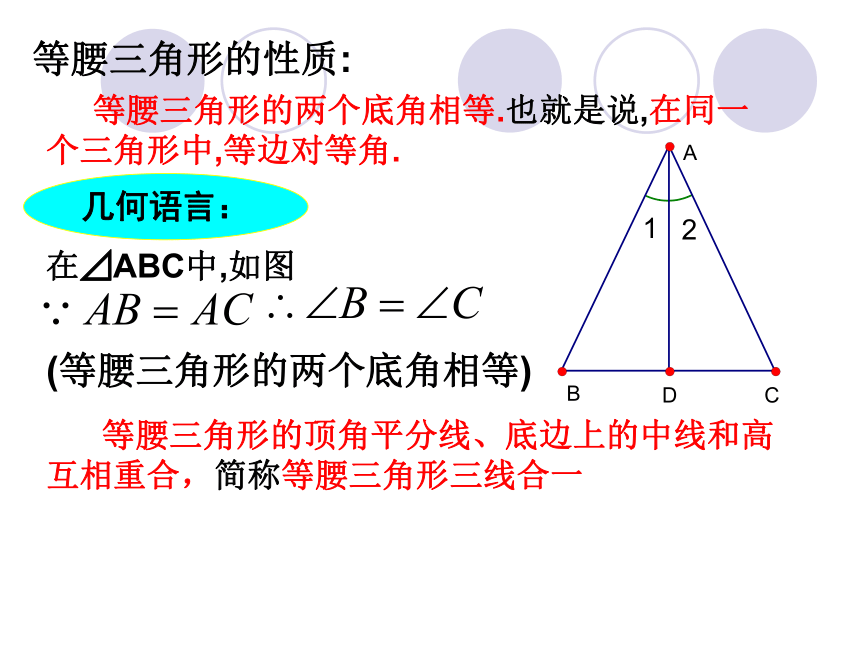
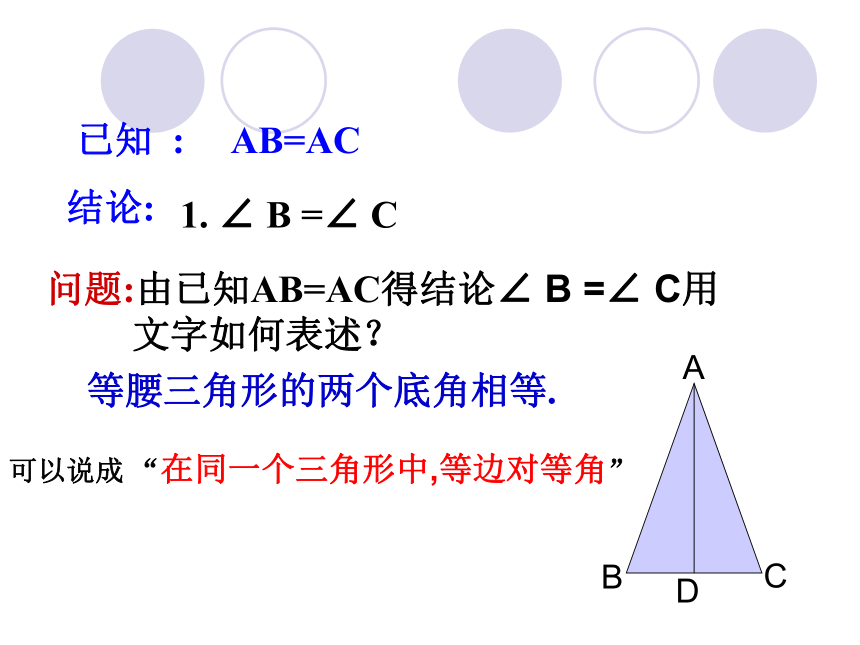
∠ADB=∠ADC.依据:轴对称变换的性质—轴对称变换不改变图形的形状和大小.(3) 你有什么发现? 能得出等腰三角形的哪些性质?合作学习、探究新知等腰三角形的性质: 等腰三角形的两个底角相等.也就是说,在同一个三角形中,等边对等角.在⊿ABC中,如图 等腰三角形的顶角平分线、底边上的中线和高互相重合，简称等腰三角形三线合一几何语言：(等腰三角形的两个底角相等) 1. ∠ B =∠ C 问题:由已知AB=AC得结论∠ B =∠ C用
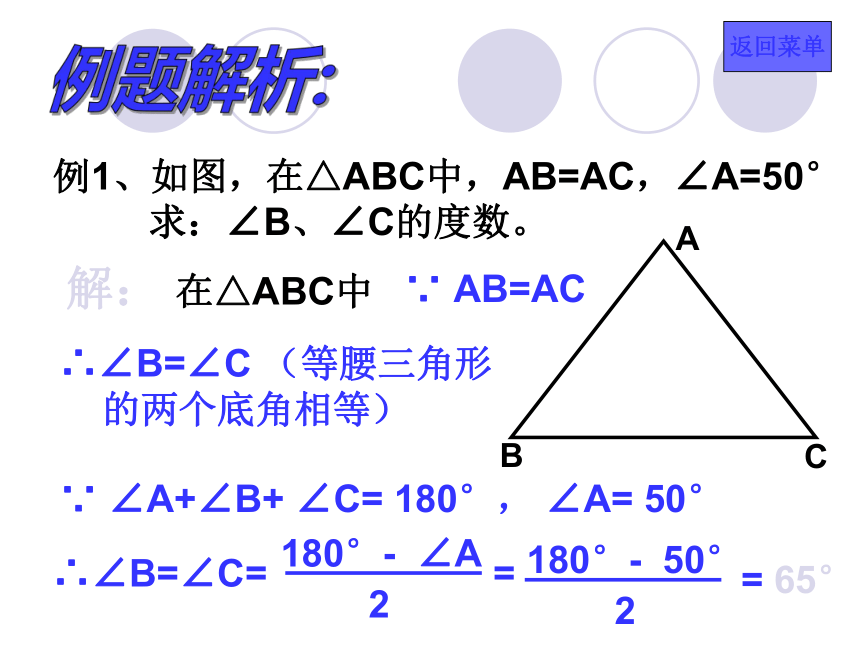
文字如何表述？等腰三角形的两个底角相等.已知 : AB=AC可以说成 “在同一个三角形中,等边对等角” 结论:例题解析:例1、如图，在△ABC中，AB=AC，∠A=50°
求：∠B、∠C的度数。解： 在△ABC中∵ AB=AC∴∠B=∠C （等腰三角形
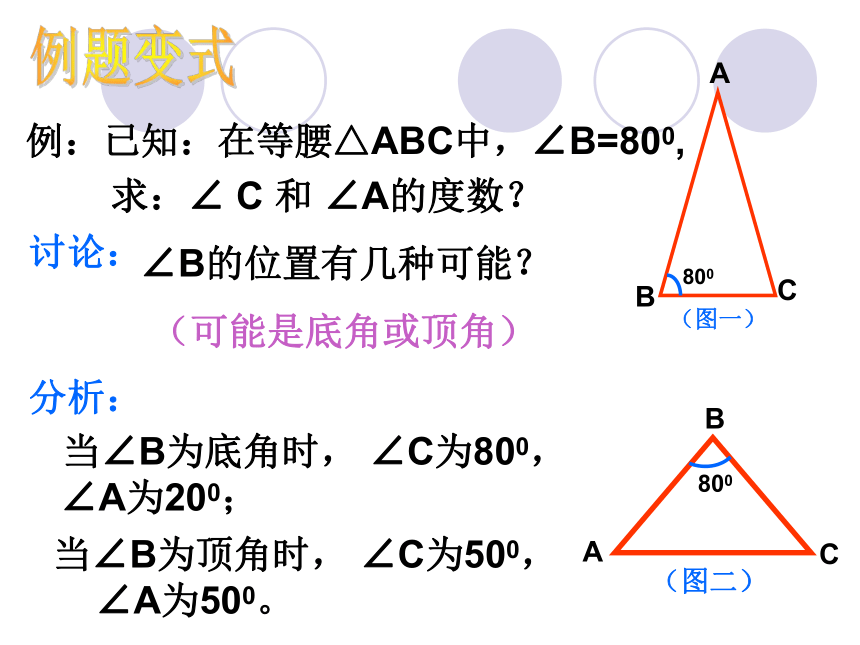
的两个底角相等）∵ ∠A+∠B+ ∠C= 180°， ∠A= 50°∴∠B=∠C== 65°返回菜单例：已知：在等腰△ABC中，∠B=800,
求：∠ C 和 ∠A的度数？例题变式（图一）讨论：∠B的位置有几种可能？
（可能是底角或顶角）分析：当∠B为底角时， ∠C为800，
∠A为200；当∠B为顶角时， ∠C为500，
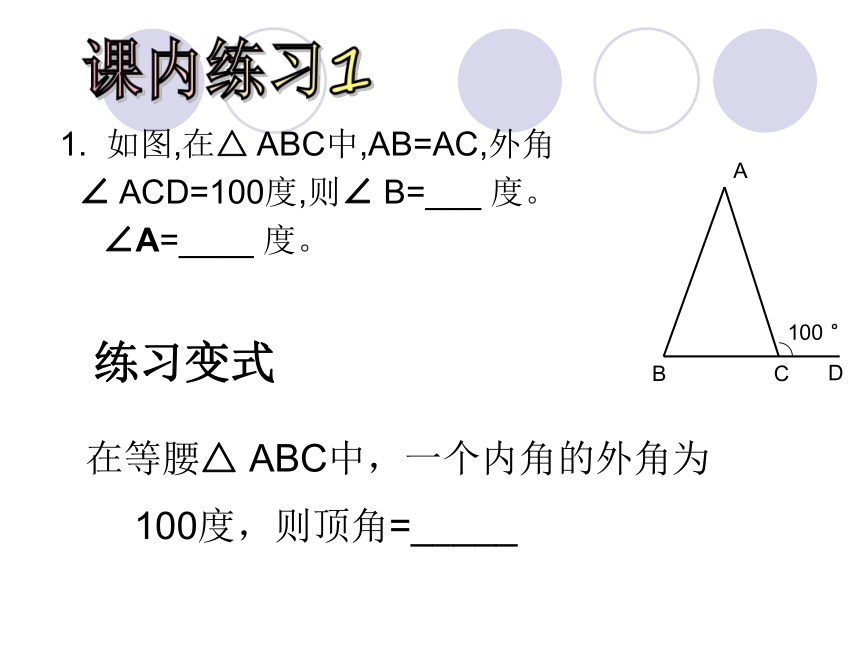
∠A为500。1. 如图,在△ ABC中,AB=AC,外角
∠ ACD=100度,则∠ B=___ 度。
　 ∠A=____ 度。
课内练习1练习变式 在等腰△ ABC中，一个内角的外角为100度，则顶角=_____重点提示等腰三角形中的内角，若没指出是底
角还是顶角应分两种情况讨论，注意
运用三角形内角之和等于180 °∵AB=AC，∠1=∠2
∴________________AD⊥BC或BD=CD∵AB=AC，AD⊥BC
∴________________∠1=∠2 或BD=CD∵AB=AC，
∴∠1=∠2 或 AD⊥BC 等腰三角形“三线合一”的性质
几何语言：__________BD=CD┓顶角平分线底边上的高底边上的中线返 回等腰三角形的性质等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合.
简称“等腰三角形三线合一”已知： AB=AC ∠1=∠2 (AD是顶角平分线).
结论：1. BD = CD, 即AD 为底边上的中线2. AD⊥BC ,即AD为底边上的高如果已知AB=AC,AD⊥BC(AD是底边上的高).那么有什么结论?如果已知AB=AC,BD=CD (AD是底边上的中线).那么有什么结论?BD=CD(AD是底边上的中线),
∠BAD=∠CAD(AD是顶角平分线).AD⊥BC(AD是底边上的高),
∠BAD=∠CAD(AD是顶角平分线)回顾问题：你能解决前面提出的问题吗？能，当重锤经过三角尺斜边的中点时，重锤
线与斜边上的高线叠合，即斜边与重锤线垂
直，所以斜边与横梁是水平的。例2 已知线段a, h(如图),用直尺和圆规作等腰三角形ABC,使底边BC=a, BC边上的高为h.作法2.如图,在等腰三角形ABC中,AB=AC,
　D为BC的中点,则点D到AB,AC的
　距离相等.请说明理由.　 课内练习228页 书上作业题第4题课堂小结等腰三角形概念性质等边对等角三线合一有两边相等的三角形腰、底、顶角、底角文字叙述几何语言等腰三角形的两底角相等（简称等边对等角）∵AB=AC
∴∠B=∠C等腰三角形顶角的平分线平分底边并且垂直于底边（简称三线合一）∵AB=AC，∠1=∠2 ∴AD⊥BC，BD=CD1、作业本2.2
2、课课练A2.2作业：3、 预习2.3, 下节课带直尺、圆规等⒈等腰三角形一个底角为70°,它的顶角为______.⒉等腰三角形一个角为70°,它的另外两个角为
__________________.⒊等腰三角形一个角为110°,它的另外两个角为___________.① 顶角+2×底角=180°② 顶角=180°－2×底角③ 底角=（180°－顶角）÷2④0°＜顶角＜180°
⑤0°＜底角＜90°结论:在等腰三角形中,40 °35 °，35 °70°,40° 或 55°,55° 巩固练习4.判断下列语句是否正确。（1）等腰三角形的角平分线、中线和高互相重合。（ ）
（2）有一个角是60°的等腰三角形，其它两个
内角也为60°. （ ）
（3）等腰三角形的底角都是锐角. （ ）
（4）钝角三角形不可能是等腰三角形 . （ ）××作业巩固练习拓展提高2.如图：在三角形ABC中，AB=AC ， D在 AC上，且BD=BC=AD，求△ABC各内角的度数？讨论：2、∠A与哪些角相等？1、∠C与哪些角相等？（∠3、 ∠ABC ）123（ ∠1、 ∠2 ）3、 ∠C与∠A是什么关系？（ ∠C=2 ∠A ）解：∵BD=AD, ∴ ∠1= ∠A∵ ∠3= ∠1+ ∠A, ∴ ∠3=2 ∠A∵ BD=BC, ∴ ∠3= ∠C, ∴ ∠C=2 ∠A∵ AB=AC, ∴ ∠ABC= ∠C=2 ∠A∵ ∠A+ ∠ABC+ ∠C=1800, ∴ 5 ∠A=1800,
∴ ∠A=360, ∴ ∠ABC= ∠C=2 ∠A=720拓展提高再见下课，再见！