《二次函数的图象与性质》说课课件
图片预览






文档简介
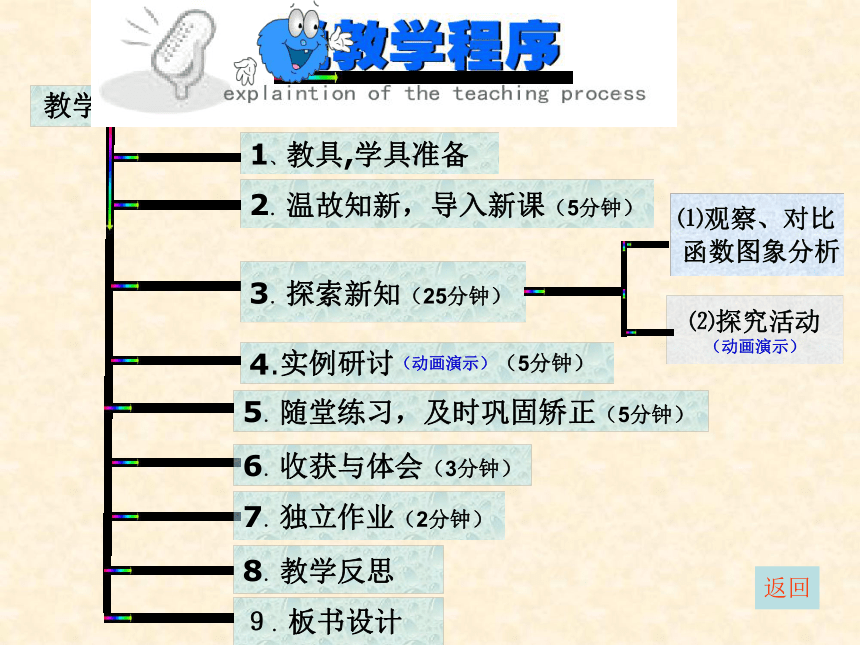
课件21张PPT。返回教学流程图6.收获与体会(3分钟) 5.随堂练习,及时巩固矫正(5分钟) 2.温故知新,导入新课(5分钟)4.实例研讨(动画演示)(5分钟) 1、教具,学具准备 7.独立作业(2分钟) 8.教学反思 ⑵探究活动
(动画演示)⑴观察、对比
函数图象分析 3.探索新知(25分钟) 9.板书设计 表格归纳动画
演示返回1、教具,学具准备
教具:多媒体演示课件.
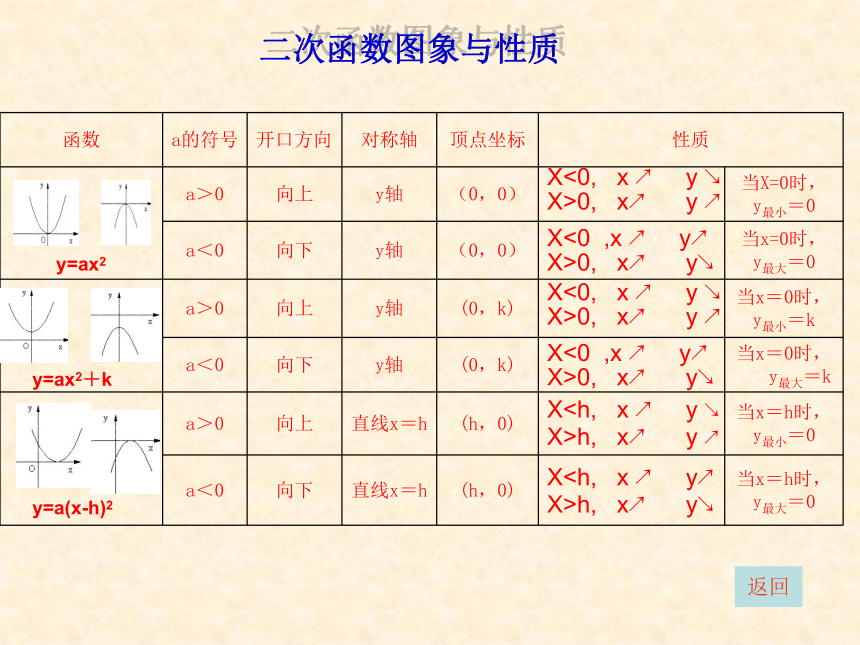
学具:方格纸。 返回y=a(x-h)2y=ax2+ky=ax2二次函数图象与性质XX>h, x↗ y↘XX>h, x↗ y ↗X<0, x ↗ y ↘
X>0, x↗ y ↗X<0, x ↗ y ↘
X>0, x↗ y ↗X<0 ,x ↗ y↗
X>0, x↗ y↘X<0 ,x ↗ y↗
X>0, x↗ y↘返回(3)探究活动问题2: 问题3: 问题4: 几何画板(3)探究活动问题1: 问题2: 问题3: 问题4: 几何画板(3)探究活动问题1: 问题2: 问题3: 问题4: 几何画板(0,0)(2,0)y轴(直线x=0)直线x=2在x轴(直线y=0)的上方
(除顶点外)向上当x=0 时,最小值为0。当x=2 时,最小值为0。(2,1)直线x=2在x轴(直线y=0)的上方
(除(2,0)点外)在x轴(直线y=1)的上方
(除(2,1)点外)向上向上当x=2 时,最小值为1 。右21上X<0 ,x ↗ y ↘
X>0, x↗ y ↗ ↘X<1, x ↗ y ↘
X>1, x↗ y ↗ X<1, x ↗ y ↘
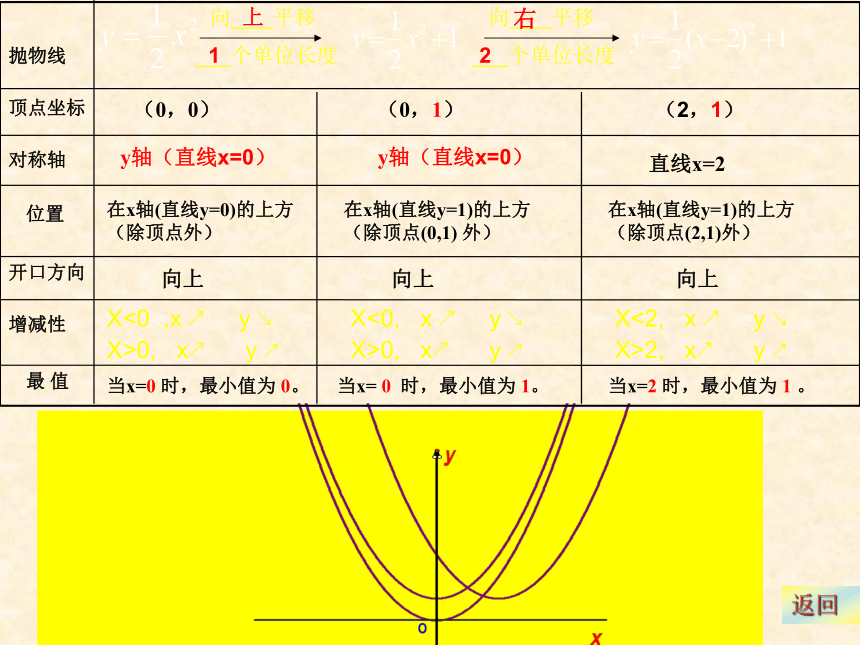
X>1, x↗ y ↗(0,0)(0,1)y轴(直线x=0)y轴(直线x=0)在x轴(直线y=0)的上方
(除顶点外)向上当x=0 时,最小值为 0。当x= 0 时,最小值为 1。(2,1)直线x=2在x轴(直线y=1)的上方
(除顶点(0,1) 外)在x轴(直线y=1)的上方
(除顶点(2,1)外)向上向上当x=2 时,最小值为 1 。上12右X<0 ,x ↗ y ↘
X>0, x↗ y ↗X<0, x ↗ y ↘
X>0, x↗ y ↗X<2, x ↗ y ↘
X>2, x↗ y ↗返回当x=2 时,最大值为 1 。(0,0)(2,0)y轴(直线x=0)直线x=2在x轴(直线y=0)的下方
(除顶点外)向下当x=0 时,最大值为 0。当x=2 时,最大值为 0。(2,1)直线x=2在x轴(直线y=0)的下方
(除顶点(2,0) 外) 直线y=1的下方
(除顶点(2,1) 外)向下向下右21上X<0 ,x ↗ y↗
X>0, x↗ y↘X<2, x ↗ y↗
X>2, x↗ y↘X<2, x ↗ y↗
X>2, x↗ y↘当x=2时,最大值为1 。(0,0)(0,1)y轴(直线x=0)y轴(直线x=0)在x轴(直线y=0)的下方
(除顶点外)向下当x=0时,最大值为0。当x=0时,最大值为1。(2,1)直线x=2在直线y=1的下方
(除顶点(0,1) 外)在直线y=1的下方
(除顶点(2,1) 外)向下向下上12右X<0 ,x ↗ y↗
X>0, x↗ y↘X<0, x ↗ y↗
X>0, x↗ y↘X<2, x ↗ y↗
X>2, x↗ y↘返回设计目的:为了加深对新知识的理解和应用,我通过板书示范,让学生注意解题的规范性。返回5.随堂练习,及时巩固矫正 ⑴题组一:
课后P13练习第1、2、3题;
⑵题组二:
课后P13练习第4题。设计目的:为了及时巩固,根据学生认知规律,设计成两组有梯度的课堂
练习题,并针对学生的解答,
正确地进行评价,出现
问题及时矫正。返回①本课学习了什么形式的二次函数?
②画二次函数图象时,列表应注意什么?
③它与前面所学的二次函数有何关系?
④它的图象的开口方向、顶点坐标、对
称轴、性质分别是什么?设计目的:我利用师生互动的方式,
帮助学生全面的理解、掌握所学知识,
进一步落实教学目标。返回设计目的:为了关注学生的个体差异,我设置必做题和提高题,使每一个学生都有成功的体验,得到相应的提高与发展,体现了“人人学有价值的数学,人人都能获得必需的数学” 的新课改理念这一宗旨.返回①学生的课堂作图作品不理想,有必要老师自己黑板画一副;
②画二次函数图象时,列表取值时学生不会选或随便选,此时应建议根据二次函数图象的对称性选用计算简单的数据,随后体验;
③为提高师生互动时,调节好少部分学生反映过于活跃。
④学生难于适应由生动、具体、形象向抽象概括的思维转变。返回设计目的:我通过反思在教学活动中的事件,理性检查与总结,进一步提高教学效果和教学水平,推动新课程改革。
屏幕3、例题 :
(解题过程略)。返回E-mail: chengzuluan@163.com祝:
老师们工作顺利!
身体健康!谢谢大家 最后我用美国著名教育家布鲁纳的一句话结束我今天的说课:“探索是数学教学的生命线”.祝:
老师们工作顺利!
身体健康!
(动画演示)⑴观察、对比
函数图象分析 3.探索新知(25分钟) 9.板书设计 表格归纳动画
演示返回1、教具,学具准备
教具:多媒体演示课件.
学具:方格纸。 返回y=a(x-h)2y=ax2+ky=ax2二次函数图象与性质X
X>0, x↗ y ↗X<0, x ↗ y ↘
X>0, x↗ y ↗X<0 ,x ↗ y↗
X>0, x↗ y↘X<0 ,x ↗ y↗
X>0, x↗ y↘返回(3)探究活动问题2: 问题3: 问题4: 几何画板(3)探究活动问题1: 问题2: 问题3: 问题4: 几何画板(3)探究活动问题1: 问题2: 问题3: 问题4: 几何画板(0,0)(2,0)y轴(直线x=0)直线x=2在x轴(直线y=0)的上方
(除顶点外)向上当x=0 时,最小值为0。当x=2 时,最小值为0。(2,1)直线x=2在x轴(直线y=0)的上方
(除(2,0)点外)在x轴(直线y=1)的上方
(除(2,1)点外)向上向上当x=2 时,最小值为1 。右21上X<0 ,x ↗ y ↘
X>0, x↗ y ↗ ↘X<1, x ↗ y ↘
X>1, x↗ y ↗ X<1, x ↗ y ↘
X>1, x↗ y ↗(0,0)(0,1)y轴(直线x=0)y轴(直线x=0)在x轴(直线y=0)的上方
(除顶点外)向上当x=0 时,最小值为 0。当x= 0 时,最小值为 1。(2,1)直线x=2在x轴(直线y=1)的上方
(除顶点(0,1) 外)在x轴(直线y=1)的上方
(除顶点(2,1)外)向上向上当x=2 时,最小值为 1 。上12右X<0 ,x ↗ y ↘
X>0, x↗ y ↗X<0, x ↗ y ↘
X>0, x↗ y ↗X<2, x ↗ y ↘
X>2, x↗ y ↗返回当x=2 时,最大值为 1 。(0,0)(2,0)y轴(直线x=0)直线x=2在x轴(直线y=0)的下方
(除顶点外)向下当x=0 时,最大值为 0。当x=2 时,最大值为 0。(2,1)直线x=2在x轴(直线y=0)的下方
(除顶点(2,0) 外) 直线y=1的下方
(除顶点(2,1) 外)向下向下右21上X<0 ,x ↗ y↗
X>0, x↗ y↘X<2, x ↗ y↗
X>2, x↗ y↘X<2, x ↗ y↗
X>2, x↗ y↘当x=2时,最大值为1 。(0,0)(0,1)y轴(直线x=0)y轴(直线x=0)在x轴(直线y=0)的下方
(除顶点外)向下当x=0时,最大值为0。当x=0时,最大值为1。(2,1)直线x=2在直线y=1的下方
(除顶点(0,1) 外)在直线y=1的下方
(除顶点(2,1) 外)向下向下上12右X<0 ,x ↗ y↗
X>0, x↗ y↘X<0, x ↗ y↗
X>0, x↗ y↘X<2, x ↗ y↗
X>2, x↗ y↘返回设计目的:为了加深对新知识的理解和应用,我通过板书示范,让学生注意解题的规范性。返回5.随堂练习,及时巩固矫正 ⑴题组一:
课后P13练习第1、2、3题;
⑵题组二:
课后P13练习第4题。设计目的:为了及时巩固,根据学生认知规律,设计成两组有梯度的课堂
练习题,并针对学生的解答,
正确地进行评价,出现
问题及时矫正。返回①本课学习了什么形式的二次函数?
②画二次函数图象时,列表应注意什么?
③它与前面所学的二次函数有何关系?
④它的图象的开口方向、顶点坐标、对
称轴、性质分别是什么?设计目的:我利用师生互动的方式,
帮助学生全面的理解、掌握所学知识,
进一步落实教学目标。返回设计目的:为了关注学生的个体差异,我设置必做题和提高题,使每一个学生都有成功的体验,得到相应的提高与发展,体现了“人人学有价值的数学,人人都能获得必需的数学” 的新课改理念这一宗旨.返回①学生的课堂作图作品不理想,有必要老师自己黑板画一副;
②画二次函数图象时,列表取值时学生不会选或随便选,此时应建议根据二次函数图象的对称性选用计算简单的数据,随后体验;
③为提高师生互动时,调节好少部分学生反映过于活跃。
④学生难于适应由生动、具体、形象向抽象概括的思维转变。返回设计目的:我通过反思在教学活动中的事件,理性检查与总结,进一步提高教学效果和教学水平,推动新课程改革。
屏幕3、例题 :
(解题过程略)。返回E-mail: chengzuluan@163.com祝:
老师们工作顺利!
身体健康!谢谢大家 最后我用美国著名教育家布鲁纳的一句话结束我今天的说课:“探索是数学教学的生命线”.祝:
老师们工作顺利!
身体健康!
