三角形的中位线

课件16张PPT。1、理解三角形中位线的概念，掌握三角形中位线定理，会用定理进行论证和计算。
2、培养学生的观察能力，形象思维和逻辑思维能力。
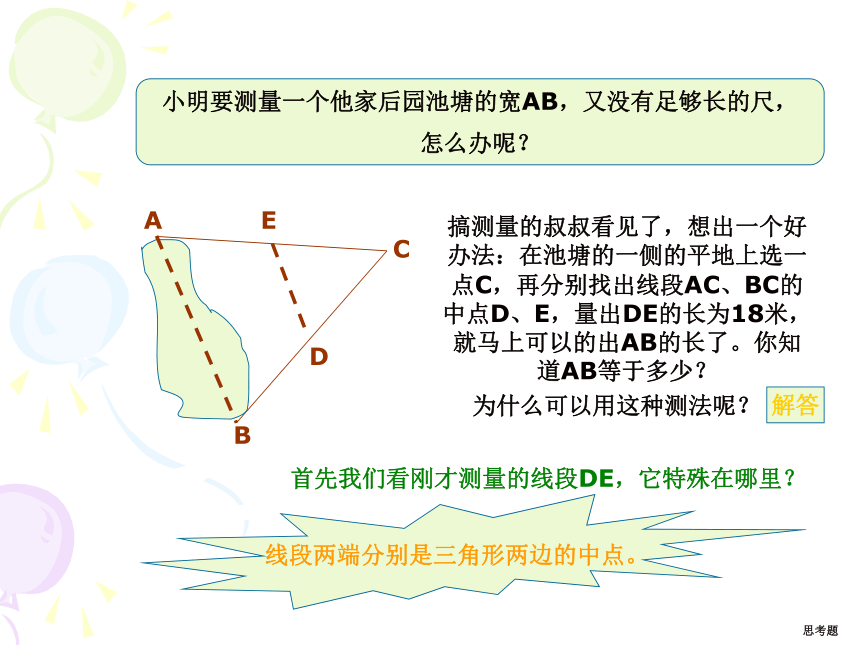
3、激发学习兴趣，培养创新精神。教学目的：小明要测量一个他家后园池塘的宽AB，又没有足够长的尺，
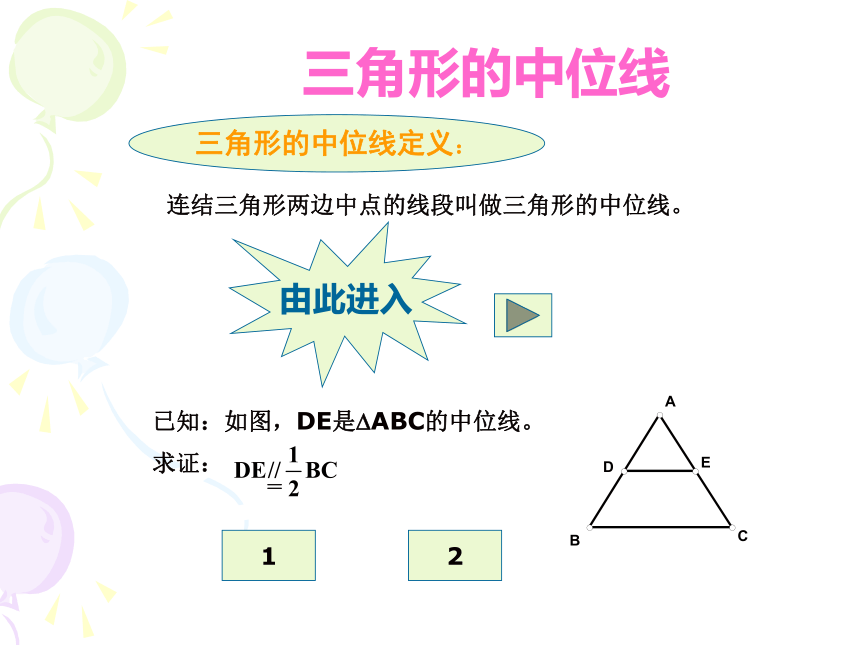
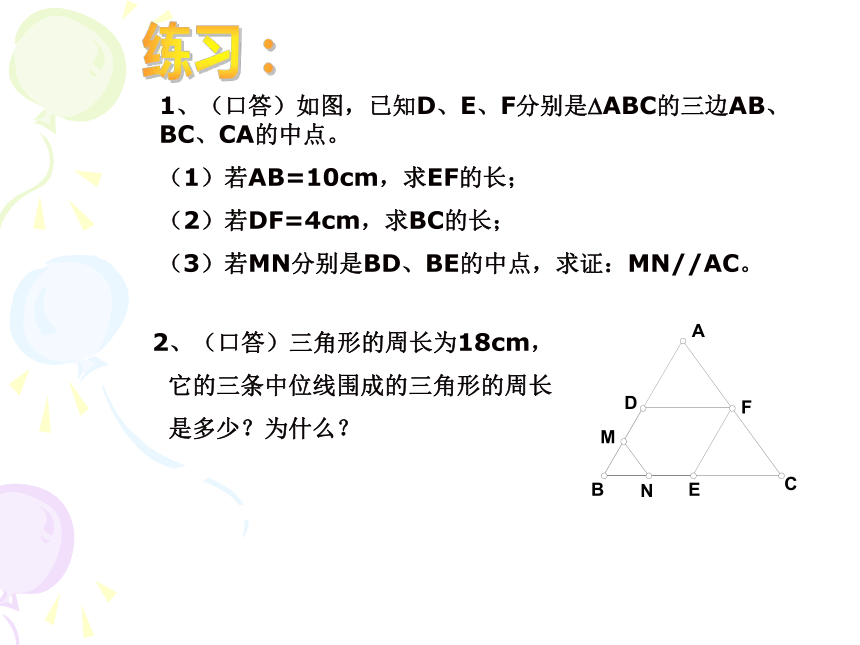
怎么办呢？搞测量的叔叔看见了，想出一个好办法：在池塘的一侧的平地上选一点C，再分别找出线段AC、BC的中点D、E，量出DE的长为18米，就马上可以的出AB的长了。你知道AB等于多少？为什么可以用这种测法呢？首先我们看刚才测量的线段DE，它特殊在哪里？ 线段两端分别是三角形两边的中点。解答思考题三角形的中位线由此进入连结三角形两边中点的线段叫做三角形的中位线。三角形的中位线定义：已知：如图，DE是?ABC的中位线。21问：一个三角形有几条中位线？答：三条。问：三角形的中位线与三角形中线有什么区别？答：中线是连结三角形一个顶点和它对边中点的线段。 中位线是连结三角形两边中点的线段。注意：这个定理在同一题设下有两个结论，在应用时要加以选择，有时需位置关系，有时需数量关系，有时需兼而有之。问：刚才量池塘宽应用的是哪种关系？AB有多宽？答：应用数量关系，三角形的中位线等于第三边的一半。 AB=36米。练习：2、（口答）三角形的周长为18cm，
它的三条中位线围成的三角形的周长
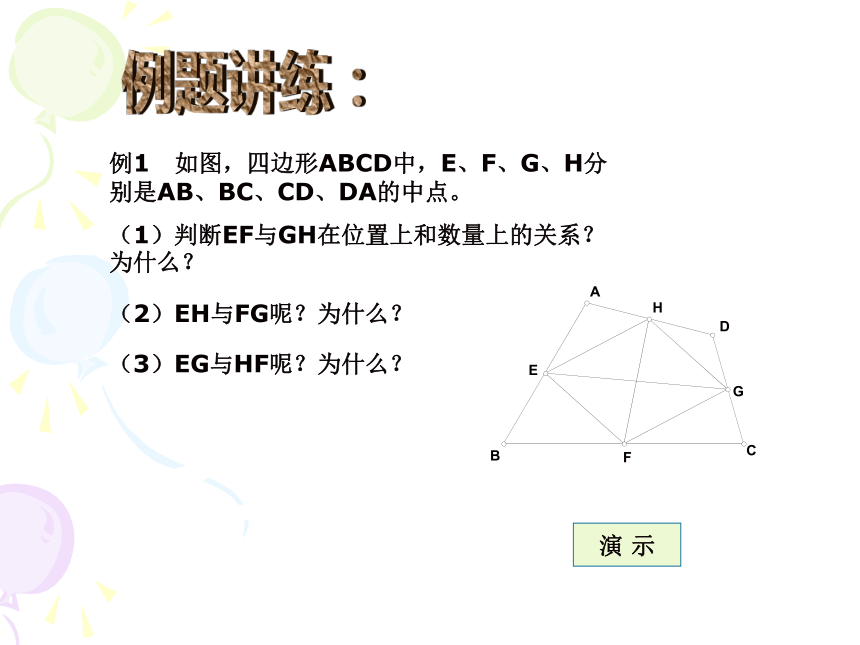
是多少？为什么？例题讲练：（2）EH与FG呢？为什么？（3）EG与HF呢？为什么？演 示巩固练习：演 示（1）四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点。同学们分组讨论！抢答题：（1）四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点。 ?如图，若四边形ABCD是平行四边形时，四边形EFGH是什么四边形？为什么？ ?如图，若四边形ABCD是矩形时，四边形EFGH是什么四边形？为什么？ ?如图，若四边形ABCD是菱形时，四边形EFGH是什么四边形？为什么？ ?如图，若四边形ABCD是正方形时，四边形EFGH是什么四边形？为什么？ ?如图，若四边形ABCD是等腰梯形时，四边形EFGH是什么四边形？为什么？演 示课堂练习：认真思考，
作在课堂作业本上！本课小结：1、本节课在同学们的大胆猜想和积极思维下完成。希以后继续
发扬。2、注意严格区别三角形的中位线与三角形的中线。3、三角形中位线定理一般运用于证明两直线平行和线段的相等、
倍分。应用此定理解题时，注意：（1）有连结点的线段但没有三角形，需完善三角形；
（2）有三角形中点没中位线，需作中位线。通过这样的转化，好多问题可迎刃而解。本课小结：4、中点四边形的形状与两对角线的位置、数量有关。一般有下列情况：一般的平行四边形矩形菱形正方形思考题：谢谢大家！已知：如图，DE是?ABC的中位线。证明过程
板书于黑板。已知：如图，DE是?ABC的中位线。证明过程
略。