二次函数复习课件（公开课）

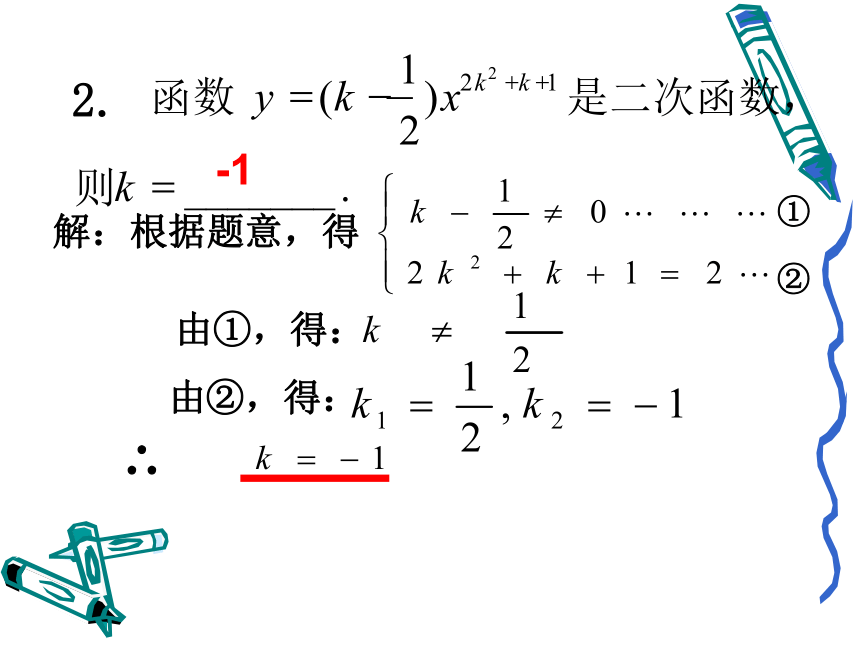
课件17张PPT。二次函数复习课二次函数复习课欢迎指导!一、二次函数的定义 1.定义：一般地,形如 y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数.2.定义要点:
(1)关于x的代数式一定是整式,a,b,c为常数,且a≠0.
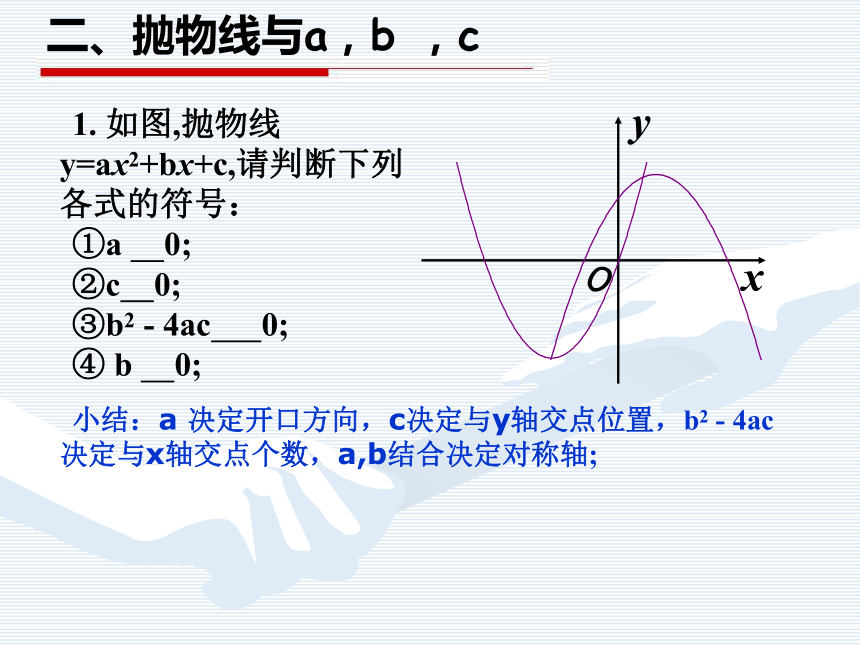
(2)等式的右边最高次数为2,可以没有一次项和常数项,但不能没有二次项.1.下列函数中,哪些是二次函数?做一做:是不是是是不是①②由①，得：由②，得：∴解：根据题意，得-11. 如图,抛物线y=ax2+bx+c,请判断下列各式的符号：
①a 0;
②c 0;
③b2 - 4ac 0;
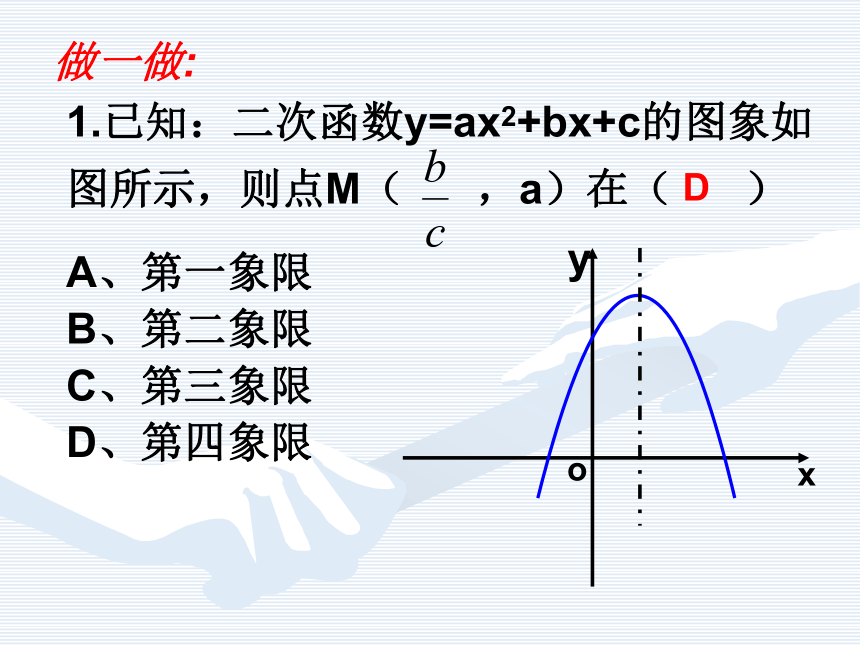
④ b 0;xyO二、抛物线与a，b ，c小结：a 决定开口方向，c决定与y轴交点位置，b2 - 4ac决定与x轴交点个数，a,b结合决定对称轴;做一做:1.已知：二次函数y=ax2+bx+c的图象如图所示，则点M（ ，a）在（ ）A、第一象限
B、第二象限
C、第三象限
D、第四象限 xoyD2.如图1所示，二次函数y=ax2+bx+c的图像开口向上，图像经过点（－1，2）和（1，0）且与y轴交于负半轴.
第（1）问：给出四个结论：①a>0；②b>0;③c>0；④a+b+c=0，其中正确的结论的序号是 . 第（2）问：给出四个结论：①abc<0；②2a+b>0;③a+c=1;④a>1.其中正确的结论的序号是_______.思路点拨：本题考查同学们的识图能力.第（2）问要求我们具有一定推理能力.
由（1）知a＞0，b＜0，c＜0；∴abc＞0；
又对称轴 ＜1， ∴2a+b ＞ 0；
∵（-1，2），（1，0）在抛物线上，
代入解析式得
①+②得a+c=1，得a=1-c，∵c ＜ 0∴1-c ＞ 1，即a ＞ 1.第（1）问中观察函数图像得：
图像开口向上决定a＞0；
对称轴 ＞0，可得b＜0；
x=0时， y＜0，即c ＜0；
由x=1时，y=0，得a+b+c=0.①④②③④1.下列各图中可能是函数
与 ( )的图象的是( )小结：双图象的问题，寻找自相矛盾的地方。即由一个图象得出字母的正负性，再去检验这个字母的符号是否适合另一个图象思维拓展√1、二次函数y=ax2+bx+c(a≠0)与一次函数y=ax+c在同一坐标系内的大致图象是（　　）xyoxyoxyoxyo(C)(D)(B)(A)C变式1：2.（09烟台）二次函数y=ax2+bx+c(a≠0)的图象如图所示，则一次函数 与反比例函数 在同一坐系内的图象大致为（ ）D变式2：三、抛物线的平移 二次函数y=ax2、y=a（x+m）2、y=a（x+m）2+k的平移规律m决定左右平移，k 决定上下平移口诀：左右平移在括号，上下平移在末梢；
左上“+”，右下“-”Y=（x-4）2+5是由哪条抛物线经怎样平移得到？Y=x2-8x+21是由哪条抛物线经怎样平移得到的？
1、(09年上海市)将抛物线向上平移一个单位后，得到新的抛物线，
那么新的抛物线的表达式是 （ ） 2.（09年鄂州)把抛物线 的图象先向右平移3个单位，再向下平移2个单位，所得的图象的解析式是，
则a+b+c=__________做一做:四.会用待定系数法求二次函数的解析式 求抛物线解析式的三种方法y=ax2+bx+c(a≠0)y=a(x-h)2+k(a≠0)y=a(x-x1)(x-x2) (a≠0)练习:根据下列条件，求二次函数的解析式。(1)、图象经过(0，0)， (1，-2) ， (2，3) 三点；(2)、图象的顶点(2，3)， 且经过点(3，1) ；(3)、图象经过(0，0)， (12，0) ，且最高点
的纵坐标是3 。问题2这位同学身高1.7 m,若在这次跳投中，球在头顶上方0.25 m处出手，问：球出手时，他跳离地面的高度是多少？如图，有一次,我班某同学在距篮下4m处跳起投篮，球运行的路线是抛物线，当球运行的水平距离2.5m时，达到最大高度3.5m，然后准确落入篮圈。已知篮圈中心到地面的距离为3.05m. 3.05 m2.5m3.5m问题1 建立如图所示的直角坐标系，求抛物线的解析式；4 m学以致用体会.分享说说这节课的收获和体验
让大家与你分享y=ax2+bx+c(a≠0)y=a(x-x1)(x-x2) (a≠0)y=a(x-h)2+k(a≠0)谢谢指导!①求k的值参考答案>1.5所以，这个小朋友不会受到伤害。B